[백준 2263] 트리의 순회

🔗 알고리즘 문제

문제 아이디어를 떠올리기가 나름 힘들었던 문제이다. 트리의 전위, 후위, 중위 탐색에 대해 잘 이해할 수 있도록 도와준 문제이다.

문제 분석

이 문제는 어떤 트리의 중위 순회한 결과와 후위 순회한 결과가 주어질 때, 해당 트리를 전위 순회 하였을 때 결과를 출력하면 된다.

중위 순회 : 4 2 5 1 6 3 7
후위 순회 : 4 5 2 6 7 3 1

다음과 같은 결과가 주어질 때, 트리의 모양은

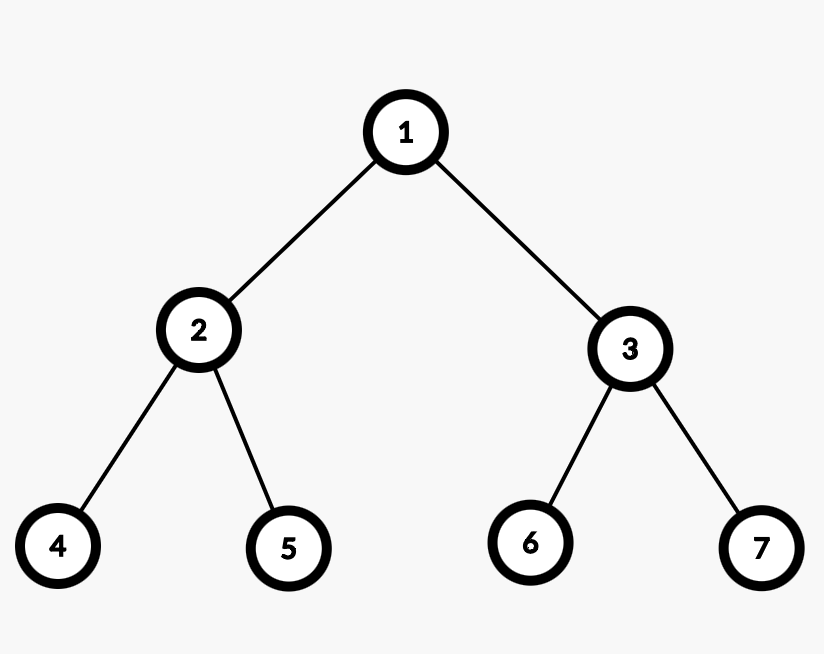
다음과 같은데, 이를 전위 순회한 결과인 1 2 4 5 3 6 7을 출력하면 된다.

발상 & 알고리즘 설계

후위 순회는 가장 마지막에 루트를 탐색하게 되므로 후위 순회의 가장 마지막 부분이 루트임을 알 수 있다.

루트를 찾고 나면 중위 순회를 한 결과에서 루트를 기준으로 왼쪽 트리, 오른쪽 트리를 나눌 수 있다.

중위 순회 : 4 2 5 1 6 3 7
후위 순회 : 4 5 2 6 7 3 1

다음과 같은 결과가 주어질 때, 전체 트리의 루트는 후위 순회 결과의 가장 마지막인 1이 되고, 중위 순회를 한 결과에서 왼쪽 트리와 오른쪽 트리를 나눈다면

왼쪽 트리는 4 2 5 오른쪽 트리는 6 3 7이 된다.

더 이상 트리가 나누어지지 않을 때까지 트리를 나누어주며 탐색을 진행해주면 정답을 도출할 수 있다.

코드

#include<iostream>

using namespace std;

int n;

int inOrder[100001] = {};
int postOrder[100001] = {};
int idx[100001] = {};

void preOrder(int left, int right, int start, int end){
    if(left > right || start > end)
        return;

    int i = idx[postOrder[end]];
    int leftSize = i - left;
    cout << inOrder[i] << " ";

    preOrder(left, i - 1, start, start + leftSize - 1);
    preOrder(i + 1, right, start + leftSize, end - 1);
}

int main(){
    cin >> n;

    for(int i = 1; i <= n; i++){
        cin >> inOrder[i];
        idx[inOrder[i]] = i;
    }

    for(int i = 1; i <= n; i++){
        cin >> postOrder[i];
    }

    preOrder(1, n, 1, n);
}