알고리즘을 공부하다보면 한번쯤은 마주하게 되는 시간 복잡도(Time Complexity)와 공간 복잡도(Space Complexity) 정리하며 공부해봅시다. 😎
복잡도?
시간 복잡도와 공간 복잡도에 대해 설명하기 전에 복잡도라는 것이 무엇인지 알아야합니다.
복잡도란 간단히 말해 알고리즘의 성능을 나타내는 척도입니다. 간단히 말해 알고리즘이 얼마나 복잡한지 이 알고리즘이 얼마나 효율적인지 나타내주는 척도라고 생각하면 편합니다.
복잡도를 계산할 때 특정 알고리즘의 수행시간과 메모리 사용량을 이용하여 계산할 수 있습니다. 이 때 수행시간에 해당하는 것이 시간 복잡도, 메모리 사용량에 해당하는 것이 공간 복잡도입니다.
빅-오(Big-O) 표기법
빅-오 표기법은 복잡도를 표기할 때 사용되는 표기법 중 가장 자주 사용되는 표기법입니다.
빅-오 표기법이 가장 많이 사용되는 이유는 최악의 경우를 생각하기가 가장 쉽기 때문인데, 빅-오 표기법은 상한선을 기준으로 효율성을 표기하여 값이 클수록, 그래프가 높을수록 비효율적이라는 것을 알 수 있습니다.
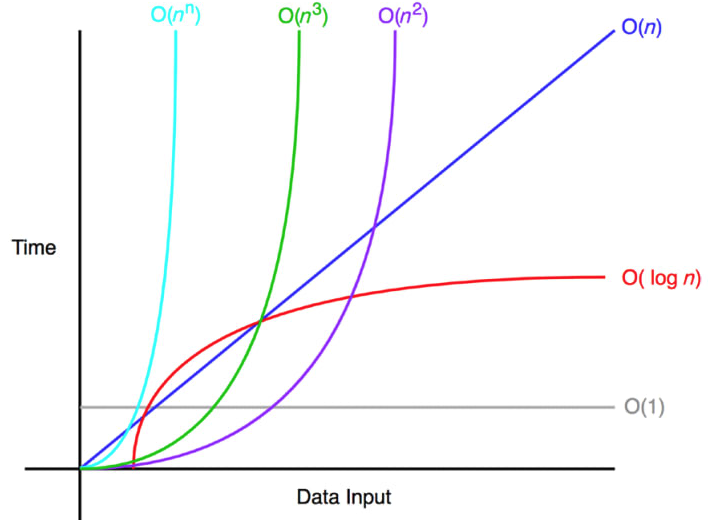
여기서
n은 입력되는 자료의 수를 나타냅니다.알고리즘의 효율성은
n의 크기에 영향을 받는다. 빅-오 표기법에서는 이미 n이 충분히 크다고 가정하기에 상수항과 같은 사소한 부분은 무시합니다.위와 같은 이유로 가장 영향령이 큰 항 이외에 영향력이 없는 항은 무시합니다
| 복잡도 | 간단 설명 | 예시 알고리즘 |
|---|---|---|
| O(1) | 일정한 복잡도라고 하며, 입력값에 관계없이 항상 동일한 시간에 결과를 얻을 수 있습니다. | 간단 입출력, Stack자료구조의 Push, Pop |
| O(n) | 선형 복잡도라고 하며, 입력값에 비례하여 선형으로 처리 시간이 증가합니다. | 1중 for문 |
| O(log n) | 로그 복잡도라고 하며, 입력값이 커질수록 처리 시간이 로그만큼 짧아집니다. | 이진 탐색 |
| O(n^2) | 2차 복잡도라고 하며, 입력값이 증가하면 처리 시간이 제곱으로 증가합니다. | 2중 for문, 삽입 정렬, 버블 정렬 |
| O(n^3) | 3차 복잡도라고 하며, 입력값이 증가하면 처리 시간이 세제곱으로 증가합니다. | 3중 for문 |
| O(n^n) | 지수 복잡도라고 하며, 입력값이 증가할수록 처리 시간이 기하급수적으로 증가합니다. | 피보나치 수열 |
FASTER
O(1)>O(log n)>O(n)>O(n^2)>O(n^3)>O(n^n)SLOWLY
시간 복잡도(Time Complexity)
시간 복잡도는 앞서 말했듯이 특정 알고리즘의 수행 시간을 의미합니다. 결과값이 같은 알고리즘이라도 코드를 어떻게 작성했느냐에 따라서 시간 복잡도가 달라질 수 있습니다. 결과값이 같다면 시간 복잡도가 적은(수행시간이 짧은) 알고리즘이 효율적인 알고리즘입니다.
시간 복잡도 표기하기
시간 복잡도를 표기할 때에는 입력값에 따른 연산 횟수를 표기하게 된다.
이름은 시간 복잡도이지만 연산 횟수를 표기하는 이유는 똑같은 코드라도 모든 OS, IDE에서 같은 결과가 나오지 않기 때문입니다.
시간 복잡도를 표기하기 위해서 정해야 할 기준이 필요한데, 이는 최선의 경우, 평균의 경우, 최악의 경우로 나뉘어져 있습니다. 대부분 최악의 경우를 기준으로 성능을 파악하게 됩니다.
ex) 시간 복잡도가 O(n)인 경우
private void function(int n) { // do something }해당 함수에서는 매개변수로 들어오는
n따라 총n번 만큼 for문이 실행됩니다. 따라서 해당 알고리즘의 시간 복잡도는 O(n)입니다.
공간 복잡도(Space Complexity)
공간 복잡도는 특정 알고리즘에서 얼마나 많은 공간(메모리)를 차지하고 있는지를 의미합니다. 컴퓨터의 발전으로 인해 예전과 달리 메모리가 풍족하여 중요도가 떨어지긴 하였지만, 많은 데이터를 컨트롤 할 경우 공간 복잡도가 커지게 되면 프로그램이 메모리에 올라가지 않아 문제가 생길 수 있습니다. 따라서 알고리즘 작성시에 공간 복잡도도 어느정도 신경써주는 것이 좋습니다.
공간 복잡도 표기하기
위에서 언급했듯이 공간 복잡도는 특정 알고리즘을 실행하는데 메모리를 얼마나 사용하게 되는지를 표기해주면 됩니다.
ex) 공간 복잡도가 O(n^2)인 경우
private void function(int n) { int** array = new int*[n]; }해당 함수는 매개변수로
n을 받아n*n크기의 2차원 배열을 동적할당 해주는 함수입니다. 총n*n개의 공간을 차지하게 되므로 해당 알고리즘의 공간 복잡도는 O(n^2)입니다.
