링크
문제
세준이는 학교에서 집으로 가려고 한다. 도시의 크기는 무한대이고, 도시의 세로 도로는 모든 정수 x좌표마다 있고, 가로 도로는 모든 정수 y좌표마다 있다. 세준이는 현재 (0, 0)에 있다. 그리고 (X, Y)에 위치한 집으로 가려고 한다. 세준이가 걸을 수 있는 방법은 두가지 인데, 하나는 도로를 따라서 가로나 세로로 한 블록 움직여서 이번 사거리에서 저 사거리로 움직이는 방법이고, 블록을 대각선으로 가로지르는 방법이 있다.
세준이가 집으로 가는데 걸리는 최소시간을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 집의 위치 X Y와 걸어서 한 블록 가는데 걸리는 시간 W와 대각선으로 한 블록을 가로지르는 시간 S가 주어진다. X와 Y는 1,000,000,000보다 작거나 같은 음이 아닌 정수이고, W와 S는 10,000보다 작거나 같은 자연수이다.
출력
첫째 줄에 세준이가 집에가는데 걸리는 최소시간을 출력한다.
풀이
처음 이 문제의 접근을 최소라고 해서 큐로 접근하였지만 패망;;;
문제를 다시 보니 최소 이동거리가 아닌 최소 시간이었다.
그렇기 때문에 수평, 대각선 이동 시간을 따져 경우의 수를 분류하여야 했다.
3가지의 방법
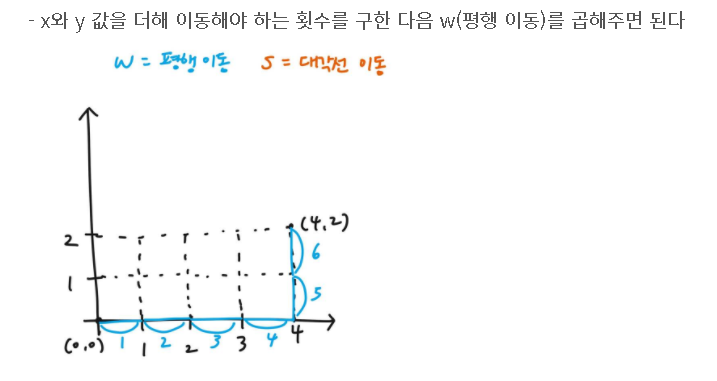
- 수평으로만 이동하는 경우
- 대각선으로만 이동하는 경우
- 대각선 + 수평을 이동하는 경우
Code
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class practice {
public static void main(String[] args) throws IOException{
// TODO Auto-generated method stub
BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st=new StringTokenizer(br.readLine());
long x=Long.parseLong(st.nextToken());
long y=Long.parseLong(st.nextToken());
long w=Long.parseLong(st.nextToken());
long s=Long.parseLong(st.nextToken());
long cost1, cost2, cost3;
//1. 수평으로만 이동하는 경우
cost1=(x+y)*w;
//2. 대각선으로만 이동하는 경우
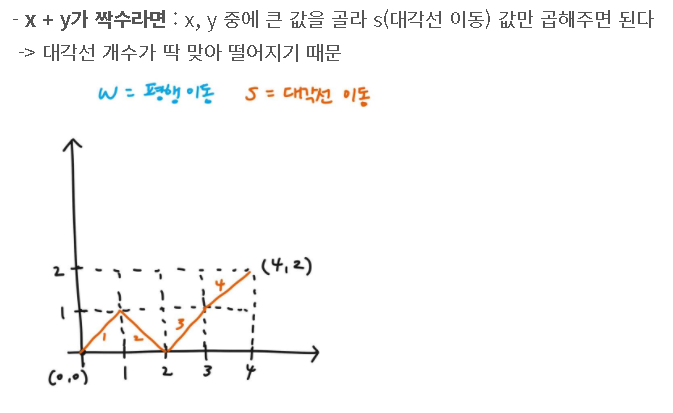
//2.1 짝수일 경우 대각선으로만 이동 가능
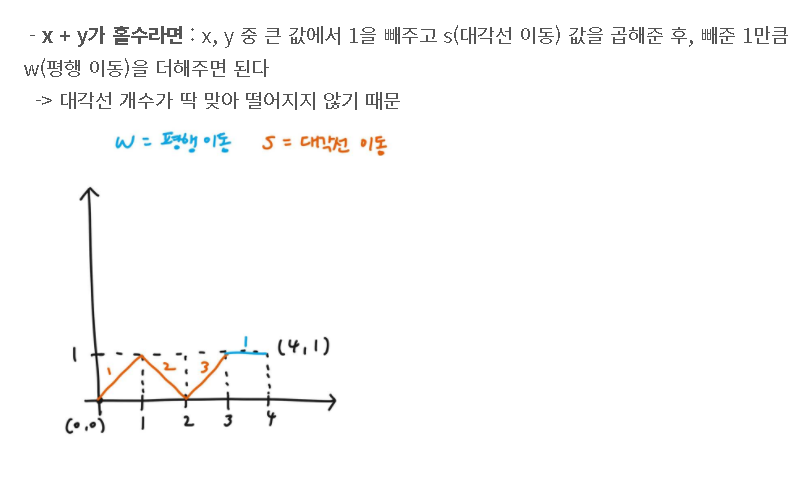
//2.2 홀수일 경우 대각선 이동 후 수평이동 한칸
if((x+y)%2==0) cost2=Math.max(x, y)*s;
else cost2=(Math.max(x, y)-1)*s+w;
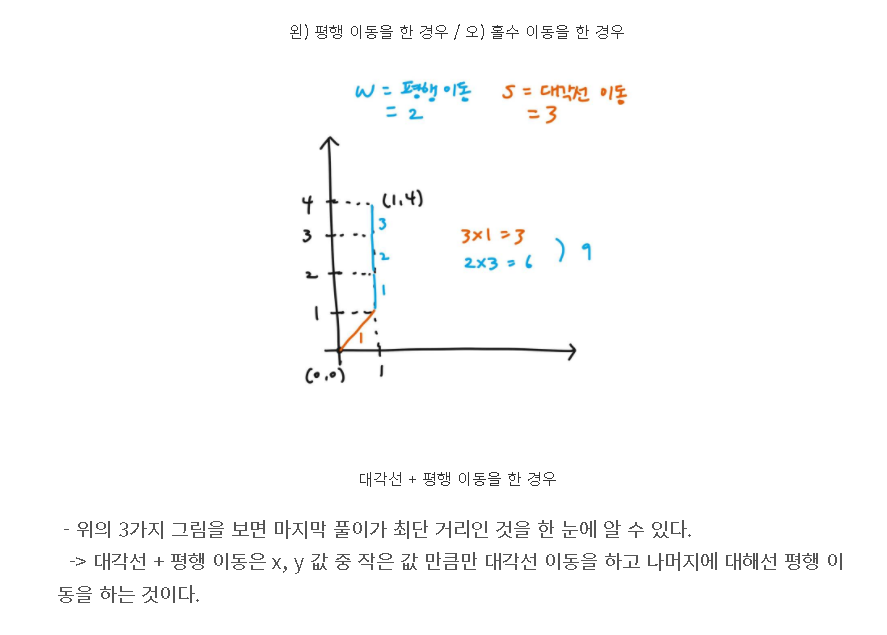
//3.대각선 + 수평 : 대각선으로 최대한 이동 후 수평 이동
cost3=(Math.min(x, y))*s+(Math.abs(x-y))*w;
System.out.println(Math.min(cost1, Math.min(cost2, cost3)));
}
}