자료구조?
여러 데이터들의 묶음을 저장하고, 사용하는 방법을 정의
데이터들을 체계적으로 정리하여 저장하는 것이, 데이터를 활용하는 것에 있어 유리함
데이터
문자, 소리 등 실생활을 구성하고 있는 모든 값
자주쓰이는 자료구조
- 스택
- 큐
- 트리
- 그래프
대부분의 자료구조는 특정한 상황에 놓인 문제를 해결하는 데 특화되어있다.
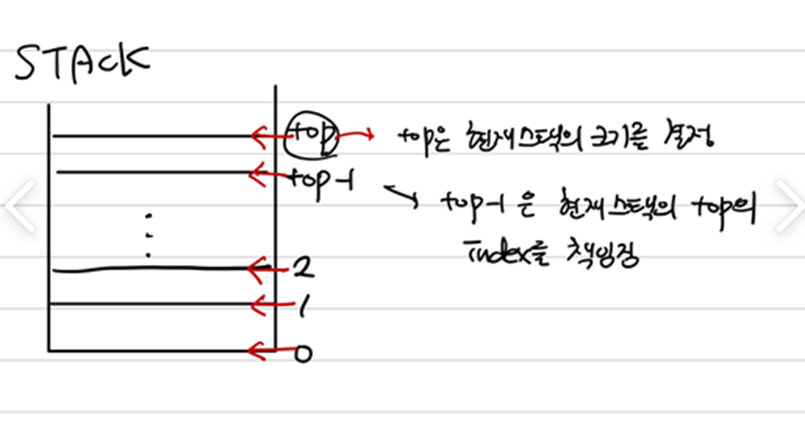
스택?
⭕ 하나의 방향으로 이루어지는 제한적 접근
-
LIFO(Last In First Out)의 구조를 가짐
-
데이터를 넣는 것을 push, 빼는 것을 pop이라 함
-
데이터는 하나씩 넣고 뺄 수 있다.
-->예시 : 브라주어의 뒤로가기 , 앞으로가기 기능
큐?
⭕ 두 개의 입출력 방향을 가지고 있다.
-
FIFO(First In First Out) 구조를 가지고 있다.
-
데이터는 하나씩 넣고 뺄 수 있다.
--> 예시 : 컴퓨터와 연결된 프린터에서 여러 문서를 순서대로 인쇄할 때 컴퓨터 장치들 사이에서 데이터를 주고 받을 때, 각 장치 사이에 존재하는 속도의 차이나 시간 차이를 극복하기 위해 임시 기억장치의 자료구조로 Queue를 사용한다. 이것을 통틀어 버퍼라고 한다.
추가 )) 원형큐
원형큐(Circular Queue)
선형큐의 단점을 보완할 수 있는 큐로는 바로 원형큐가 있습니다. 큐를 직선 형태로 놓는 것 보다 원형으로 생각해서 큐를 구현하는 것 큐를 원형으로 생각해야되기 때문에 모듈러 연산(나머지 연산)을 해야한다.
참고 : https://reakwon.tistory.com/30
추가 )) pop()과 unshift() , shift() ,push()
스택을 구현하면서 array 메소드에 대한 이해가 조금 필요했는데 .
Pop() 메소드의 개념
const Arr = [1,2,3,4];
이라할 때
Const a = arr.pop() //4가 나옴
Console.log(arr); //[1,2,3] 나옴
findIndex , Math.max()
- findIndex() 메서드는 주어진 판별 함수를 만족하는 배열의 첫 번째 요소에 대한 인덱스를 반환합니다. 만족하는 요소가 없으면 -1을 반환합니다.
- Math.max()함수는 입력값으로 받은 0개 이상의 숫자 중 가장 큰 숫자를 반환합니다.
출처 : mdn 공식문서그래프
✅ 직접적인 관계가 있는 경우 두 점을 이어주는 선이 있다.
간접적인 관계라면 몇 개의 점과 선에 걸쳐 이어진다.
하나의 점을 그래프에서는 정점(vertex)이라고 표현하고, 하나의 선은 간선(Edge)라고 한다.
-
인접 정점 : 하나의 정점에서 간선에 의해 직접 연결된 정점
-
가중치 그래프 : 연결의 강도가 얼마나 되는 지 적혀 있는 그래프
-
비가중치 그래프 : 연결의 강도가 적혀 있지 않은 그래프
-
무(방)향 그래프 : 방향이 있는 그래프는 방향 크래프 방향이 없는 그래프는 무방향 그래프
-
진입차수 : 들어오는 간선 수
-
진출 차수 : 나가는 간선 수
-
자기 루프 : 정점에서 진출하는 간선이 곧바로 자기 자신에게 진입하는 경우 (다른 정점을 안거친다.)
-
사이클 : 한 정점에서 출발해서 다른 정점을 거쳐 자기 자신에게 돌아가는 경우
인접행렬?
두 정점을 바로 이어주는 간선이 있다면, 두 정점은 인접하다고 얘기한다.
A와 B가 이어져 있다면, 1(true)
이어지지 않았다면 0 (false) 만약에 가중치 그래프면 1대신 관계에서 의미 있는 값을 저장한다.
✅ 인접행렬의 사용
-
두 정점 사이의 관계 파악
-
빠른 경로를 찾고자할 때 사용 한다.
--> 인접행렬의 사용 :
메모리를 효율적으로 사용하고 싶을 때 사용,(연결 가능한 모든 경우의 수를 저장하기 때문에 상대적으로 메모리를 많이 차지한다.)
일상생활 예시 )
사람들관의 SNS관계, 내비게이션 (길 찾기) 등에서 사용하는 자료구조가 바로 그래프이다.
🎈 알고리즘 꿀팁
Vertex를 삭제하는 것은 list를 사용하는 것이 좋고, 두 정점사이에 관계없는지 있는 지 확인하기에는 Matrix가 용이하다
트리
🔺 그래프의 여러 구조 중 단방향 그래프의 한 구조로, 하나의 뿌리로부터 가지가 사방으로 뻗은 형태이다.
-
깊이(depth) : 루트로부터 하위 계층의 특정 노드까지의 깊이
-
레벨(Level) : 같은 깊이를 갖는 노드
-
높이(height) : 리프 노드를 기준으로 루트까지의 길이
-
서브트리(Sub Tree) : 트리 구조에서 루트로부터 뻗어 나오는 큰 트리의 내부의 작은 트리
실사용 예제 ) 디렉토리 구조 , 월드컵 토너먼트 대진표, 가계도(족보), 조직도 등 이진 트리
자식 노드가 최대 두 개인 노드들로 구성된 트리
💥자료의 삽입, 삭제 방법에 따라
정 이진 트리(Full binary tree),
완전 이진 트리(Complete binary tree)
포화 이진 트리(Perfect binary tree)
BST(Binary Search Tree) 이진 탐색트리
👍 이진 탐색 트리는 모든 왼쪽 자식의 값이 루트나 부모보다 작고, 오른쪽 자식의 값이 루트나 부모보다 큰 값을 가지는 특징이 있다.
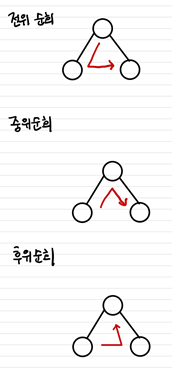
전위 순회 , 중위 순회, 후위 순회
BFS , DFS
-
DFS : 루트노드로부터 다음 자식 노드로 넘어갈 때 해당 노드의 자식노드들까지 탐색 후 리프노드까지 찾아 낸 후에 다음 분기로 넘어가는 방식
--> 최대한 깊게 내려가서, 더 이상 자식노드가 없을 경우에 옆으로 이동 -
BFS : 루트 노드에서 시작해서 인접한 노드를 먼저 탐색하는 방식
--> 최대한 형제 노드들을 탐색한 뒤, 다음이 없을 때 자식노드로 이동
--> 길찾기 같은 예시가 있음
🎈 알고리즘 꿀팁
-
방문한 곳은 재방문하지 않는다.
--> 이미 방문했으니까 방문할 필요가 없음. 길찾기 핵심 -
BFS : Queue를 알면 사용 가능하다. BFS와 친구
//queue 와 같이 친구 while, isEmpty
1. 모든 노드를 방문하고자 할 때 선택
2. 깊이 우선 탐색이 너비우선 탐색보다 더 간단
3. 검색 속도 자체는 BFS가 느리다.자료구조의 첫 날이라 코플릿을 통한 , 스택과 큐에 대한 기본적인 이해에 대한 코드, 그리고 스택과 큐를 이용한 알고리즘 예제들을 풀어보았다.
평소 스택과 큐는 어느정도 이해를 하고 있어서, 쉽게 할 수 있었으나 , 그래프와 bfs/dfs 부분에서 조금 헤맸던 것 같다.
추가 정리?
- 연결리스트
- 데크(deque)
- 해시테이블
- 힙 트리
- 우선순위 큐
자료구조 시각자료 :
https://www.cs.usfca.edu/~galles/visualization/Algorithms.html
https://visualgo.net/en
