우선 순위 큐

문제

우선순위 큐는 일반 큐와 다르게 요소의 삽입 순서(FIFO)가 아니라 우선순위에 따라 요소를 정렬하고 처리한다.

데이터에서 가장 작은 값이나 가장 큰 값을 자주 조회하고 삭제해야 하는 경우, 우선순위 큐는 O(log n) 시간 복잡도로 이를 처리할 수 있어 효율적이다.

우선 순위 큐는 실시간 서비스를 제공하는 애플리케이션에서 활용할 수 있다.
소켓(WebSocket)으로 전달되는 데이터의 타입별 우선순위와 타임스탬프를 조합하여 우선순위 큐로 관리하면, 중요도가 높은 데이터는 즉시 처리하고 덜 중요한 데이터는 대기열에 추가하여 순차적으로 처리할 수 있다.

이 외에도 애니메이션 관리, 리소스 로딩 최적화 등 다양한 상황에서 활용될 수 있다.

O(log n)
로그 시간 복잡도 O(log n)는 알고리즘이 데이터의 크기 n에 따라 굉장히 빠르게 실행되는 것을 의미한다.
한 번의 연산마다 탐색 범위를 절반씩 줄이기 때문에, 처리 시간이 매우 효율적이다.

• 데이터가 1,000개면 최대 10번의 연산
• 데이터가 1,000,000개라도 최대 20번의 연산만 필요!

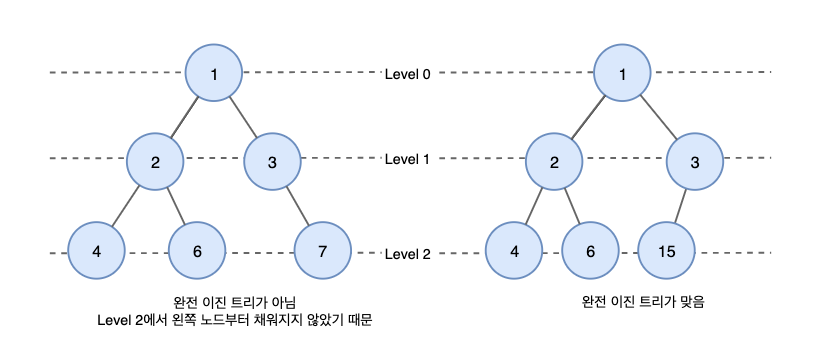
우선순위 큐는 완전 이진트리를 기반으로 구현된다.

시간 복잡도

우선 순위 큐

• 삽입(enqueue) : O(log n)
  요소를 추가할 때 힙 구조를 유지하기 위해 비교 및 교환 작업이 필요
• 제거(dequeue) : O(log n)
  최우선 요소를 제거하고 힙을 재정렬

일반 큐

• 삽입(enqueue) : O(1)
  큐의 뒤쪽에 새로운 요소를 추가하는 작업은 상수 시간.
• 제거(dequeue) : O(n)
  연결 리스트가 아닌 경우 요소를 제거한 뒤 나머지 요소를 재정렬해야 하므로 O(n) 소요

구현

class Heap {
    constructor(array = []) {
        this.heap = array.slice(); // 배열 복사
        this.#buildHeap(); // 초기 힙 빌드
    }

    /*************** 프라이빗 메소드 ***************/
    #getParentIndex(index) {
        return Math.floor((index - 1) / 2);
    }

    #getLeftChildIndex(index) {
        return 2 * index + 1;
    }

    #getRightChildIndex(index) {
        return 2 * index + 2;
    }

    #swap(index1, index2) {
        [this.heap[index1], this.heap[index2]] = [this.heap[index2], this.heap[index1]];
    }

    #buildHeap() {
        const startIndex = Math.floor(this.heap.length / 2) - 1;
        for (let i = startIndex; i >= 0; i--) {
            this.#heapifyDown(i);
        }
    }

    #heapifyUp() {
        let index = this.heap.length - 1;
        while (index > 0) {
            const parentIndex = this.#getParentIndex(index);
            if (this.compare(this.heap[parentIndex], this.heap[index])) {
                this.#swap(parentIndex, index);
                index = parentIndex;
            } else {
                break;
            }
        }
    }

    #heapifyDown(index = 0) {
        const length = this.heap.length;
        let extreme = index;

        while (true) {
            const leftChildIndex = this.#getLeftChildIndex(index);
            const rightChildIndex = this.#getRightChildIndex(index);

            if (leftChildIndex < length && this.compare(this.heap[extreme], this.heap[leftChildIndex])) {
                extreme = leftChildIndex;
            }

            if (rightChildIndex < length && this.compare(this.heap[extreme], this.heap[rightChildIndex])) {
                extreme = rightChildIndex;
            }

            if (extreme !== index) {
                this.#swap(index, extreme);
                index = extreme;
            } else {
                break;
            }
        }
    }

    /*************** 퍼블릭 메소드 ***************/
    insert(value) {
        this.heap.push(value);
        this.#heapifyUp();
    }

    remove() {
        if (this.heap.length === 0) throw new Error("Heap is empty");
        if (this.heap.length === 1) return this.heap.pop();

        const root = this.heap[0];
        this.heap[0] = this.heap.pop();
        this.#heapifyDown();
        return root;
    }

    peek() {
        if (this.heap.length === 0) throw new Error("Heap is empty");
        return this.heap[0];
    }

}

class MinHeap extends Heap {
    compare(parent, child) {
        return parent > child; // 최소 힙
    }
}

class MaxHeap extends Heap {
    compare(parent, child) {
        return parent < child; // 최대 힙
    }
}

초기 힙 빌드

초기 힙 빌드시, 원소를 하나하나 삽입하면 O(n \log n)의 시간이 소요되지만, 아래와 같은 방법으로 빌드하면 O(n)에 최적화할 수 있다.

1. 리프 노드는 작업할 필요가 없다:

• 리프 노드는 자식 노드가 없기 때문에 힙 조건(부모 ≤ 자식)을 검사하거나 교환할 필요가 없다.

• 즉, 리프 노드는 부모 노드보다 크기만 하면 된다. (최소 힙 인 경우.. 최대 힙은 그 반대)

• 리프 노드는 항상 배열의 후반부에 위치하며, 그 위치는 floor(this.heap.length / 2 ) 이다.

• 예를 들어, 배열 길이가 8이라면 리프 노드는 인덱스 4, 5, 6, 7 이다.

• heapifyDown()은 부모 노드와 자식 노드만 비교하며, 필요하면 값을 교환한다.

2. 그래서 왜 O(n)?

• heapifyDown()의 작업량은 부모 노드의 깊이에 따라 달라진다.

• 트리의 구조상, 상위 노드들은 적고, 하위 노드들은 많다는 점이 중요

• 상위 노드: 작업량은 많지만 노드 수가 적다.

• 하위 노드: 작업량은 적지만 노드 수가 많다.

• 이 균형 덕분에 전체 작업량은 O(n)에 가깝게 수렴한다.