Leet Code - Largest Rectangle On Histrogram

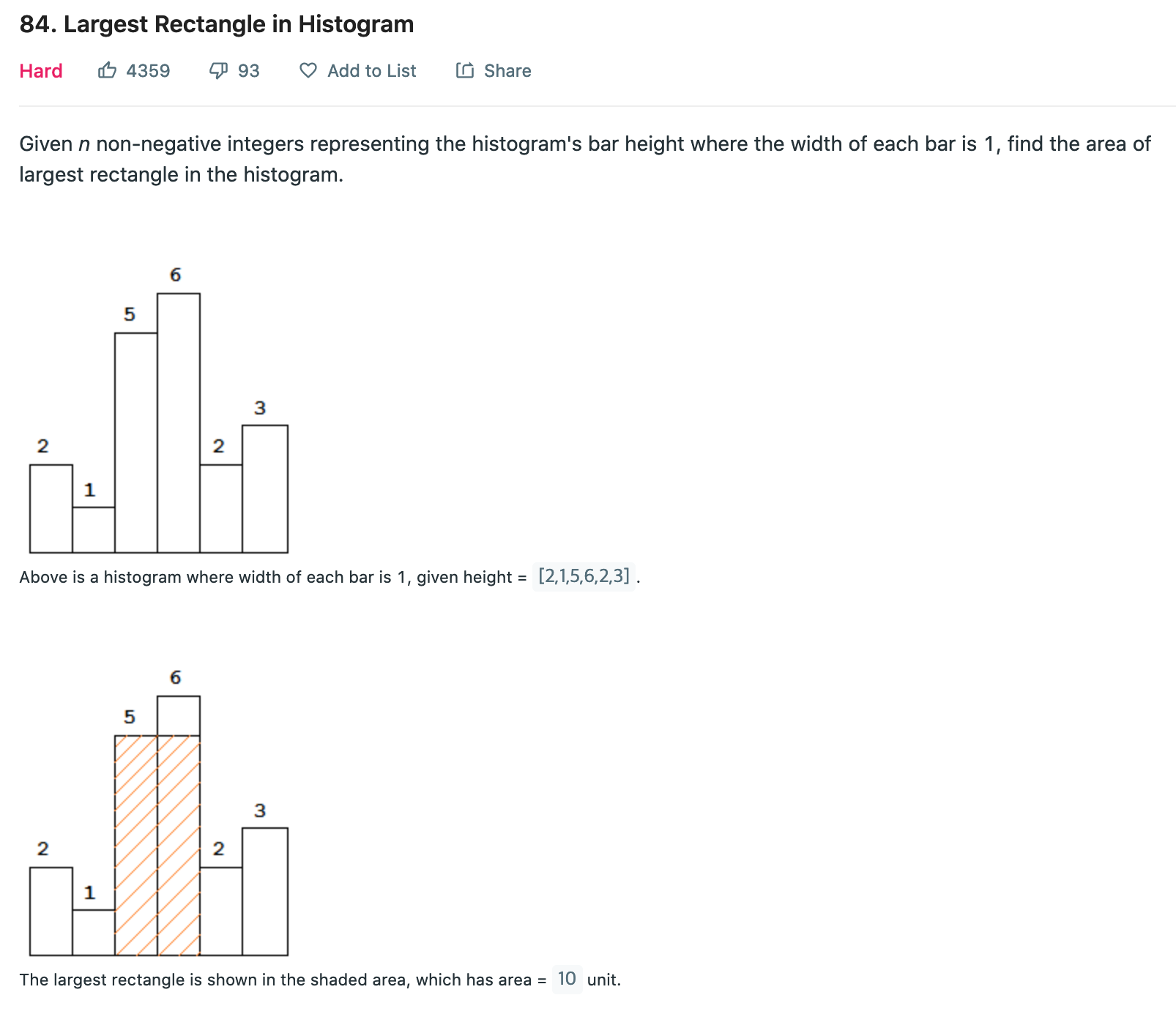
문제 설명

사각형을 수평방향으로 짜를때 가장 넓이가 큰 사각형의 값을 반환혀라.

사실 위 문제를 푸는 것 보다 거의 일주일 동안 고민하고 있는 Maximal Rectangle 을 풀기 위해 위 문제를 풀고 있다.

문제 해결 방법

1. 2Pointer 를 이용해서 $O(n^2)$으로 돌려버리는 법

2. 분할 정복법을 이용한 $O(Nlog_2n)$ 방법

3. 스택을 이용한 $O(N)$ 방법
   간단하게 서술하자면 이미 길이가 결정이 난 사각형은 필요가 없다.
   길이가 결정이 나는 조건이 왼쪽 사각형과 오른쪽 사각형의 높이가 자신보다 작은 경우 위 울타리의 조건이 끝이 나버린다.

따라서 h[i] > h[i+1] 인 경우는 길이를 결정해버리면 되고
h[i] < h[i+1] 인 경우 스택에 넣어 계산식을 이어 나가버리면 된다.

사실 1번으로 바로 해결했지만 Stack을 해결해서 풀어야 할 문제라서 풀이 방법은 2개를 제시하겠다.

소스코드

• 1번

import java.util.*;
import java.lang.*;
class Solution {
    public int largestRectangleArea(int[] heights) {
        
        int answer = 0;
        
        for(int i=0; i<heights.length; i++){
            int right = i+1;
            int left = i-1;
            int height = heights[i];
            while(left>=0&&height<=heights[left])
                left--;
            
            while(right<heights.length && height<=heights[right])
                right++;
            
            int row = right - left-1;
            int result = row * height;
            answer = Math.max(answer,result);
            
            
        }
        return answer;
        
    }
}

• 3번

import java.util.*;
import java.lang.*;
class Solution {
    public int largestRectangleArea(int[] heights) {
        Stack<Integer> stack = new Stack<>();
        int answer = 0;
        for(int i=0; i<=heights.length; i++){
            int nextHeight = i== heights.length ? 0 : heights[i];
            while(!stack.isEmpty() && heights[stack.peek()]>=nextHeight){
                int j = stack.pop();
                int width = -1;
                if(stack.isEmpty()){
                    width = i;
                }else
                    width = i-stack.peek()-1;
                int result = width * heights[j];
                answer = Math.max(result,answer);
            }
            stack.push(i);
            
        }
        return answer;
    }
}

후기

Next Challenges에 Maximal Rectangle이 보이는가..? 풀고만다.. 🔥