[알고리즘] 그래프의 깊이 우선 탐색 DFS

깊이 우선 탐색(DFS)란?

모든 정점을 발견하는 가장 단순한 방식의 탐색입니다.

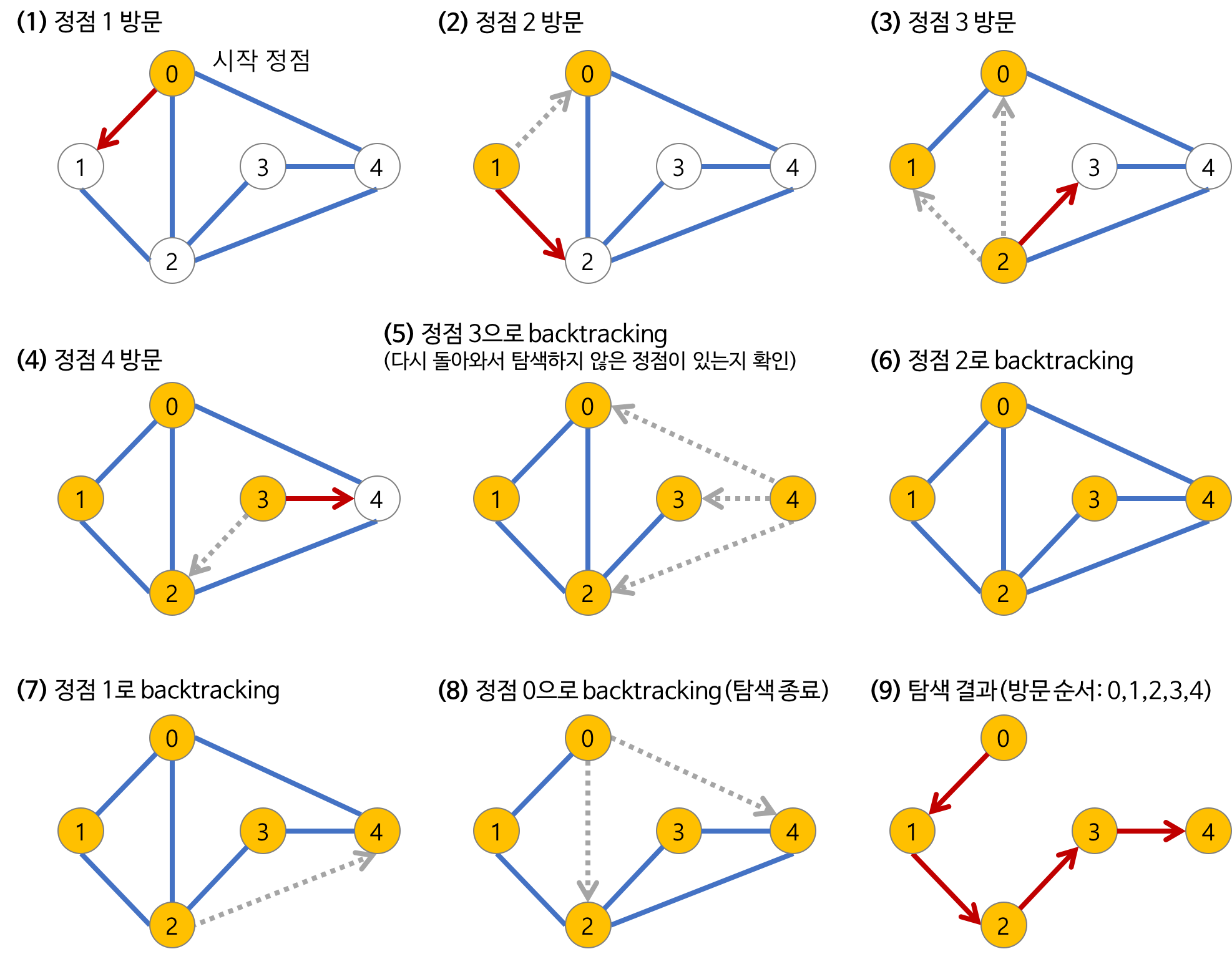
현재 정점과 인접한 간선들을 하나씩 검사하다가, 아직 방문하지 않은 정점으로 향하는 간선이 있다면 그 간선을 무조건 따라가는 것

출처 : https://gmlwjd9405.github.io/2018/08/14/algorithm-dfs.html

깊이 우선 탐색의 중요한 특징은 더 따라갈 간선이 없을 경우 이전으로 돌아간다는 점입니다

즉 이것을 구현하기 위해 지금까지 거쳐온 정점들을 모두 저장해 둬야하는데, 재귀 호출을 이용하면 간단히 해결할 수 있음

DFS의 구현

class Graph {
    private int v;
    private ArrayList<Integer>[] adjacent;
    private boolean[] isVisited;

    public Graph(int v){
        this.v = v;
        this.adjacent = new ArrayList[v];
        for(int i=0; i<adjacent.length; i++){
            adjacent[i] = new ArrayList<Integer>();
        }
    }

    public void addEdge(int v, int w){
        adjacent[v].add(w);
        //adjacent[w].add[v];  // 무향 그래프일경우
    }

    public void DFS(int start){
        isVisited = new boolean[v];
        goDFS(start);
    }

    public void goDFS(int vertex){
        System.out.print(vertex+" ");
        isVisited[vertex] = true;
        for(int next : adjacent[vertex])
            if(!isVisited[next])
                goDFS(next);
    }
}

DFS의 시간 복잡도

• 인접리스트의 시간 복잡도

  인접리스트 깊이 우선 탐색의 시간 복잡도는 $O(|V|+|E|)$입니다.

• 인접 행렬의 시간 복잡도

  인접 행렬 깊이 우선 탐색의 시간 복잡도는 $O(|V|)$ 입니다.

이유
인접 리스트의 경우 해당 vertex가 가지고 있는 리스트를 한번씩 순환 해야 되기 때문에 $O(|V|+|E|)$
만큼 걸린다.

하지만 인접 행렬일 경우 해당 vertex가 어디에 연결 되어있는지 바로 확인할 수 있기 때문에 $O(|V|)$ 만큼 시간이 걸린다.

DFS로 해결할 수 있는 문제들

두 정점이 서로 연결되어있는가 확인하기

isVisited가 true일경우 연결되어있음.

연결된 부분집합의 개수 세기

DFSAll을 구성하고 dfs가 처음에 몇번 호출되는지 갯수 세기

위상정렬

• 위상정렬이란?
  

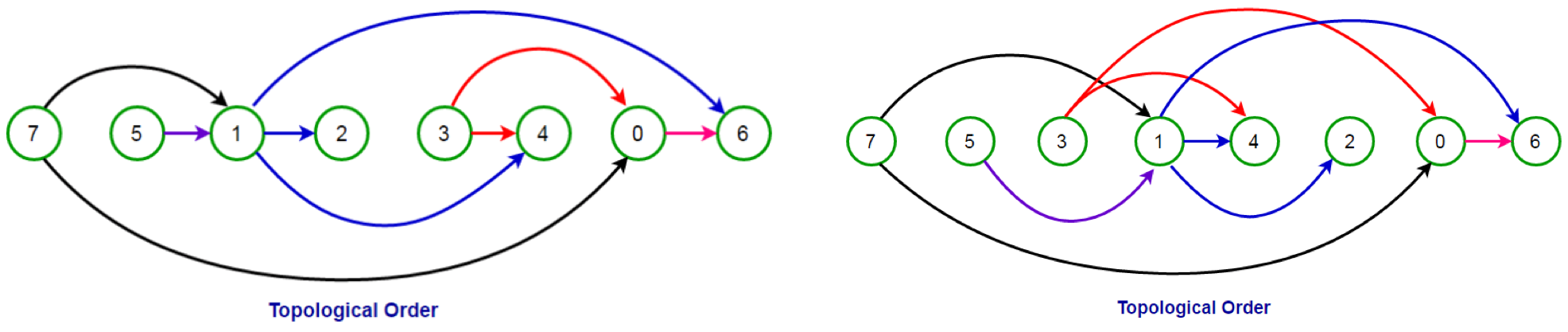
  의존성 있는 작업들이 주어질 때, 이들을 어떤 순서로 수행해야 하는지 계산하는 것.

위상정렬을 푸는 가장 직관적인 방법은 들어오는 간선이 하나도 없는 정점들을 하나씩 찾아서, 정렬 결과 뒤에 붙이고 그래프에서 이 정점을 지우는 과정을 반복하는 것이다.

그렇다면 DFS로 어떻게 해결할까?

1. DFSAll()을 수행하며 dfs()가 종료할 때마다 현재 정점의 번호를 기록
2. DFSAll()이 종료하고 기록된 순서를 뒤집으면 위상 정렬의 결과를 얻을 수 있다.

• 따라서 dfs()가 늦게 종료한 정점일수록 정렬 결과의 앞에 옵니다.

간과한점
나는 당연히 위 그래프에서 7 다음에 1을 수행해야하는 순서로 알고있었는데, 그게 아니라 1-> 7을 해야 되는 것이다.

즉 그래프에서 A->B로 표현이 된다면 B는 A보다 먼저 수행되어야 할 일의작업이다.