[알고리즘] Red-Black Tree _ 1

1. 레드블랙 트리의 기원

• 이진탐색트리의 마지막에서 살펴볼 수 있었듯이, 최악의 경우 트리의 높이가 O(N)인 경우가 있다는 사실을 확인 할 수 있었다.
  => 이 점을 반영하여, 트리의 균형이 무너지지 않도록 하여 성능을 향상 시키고자 한 트리이다.

2. 레드블랙 트리의 특징

균형잡인 트리로 높이가 O(log n)이다.
이에 따라, 삽입 / 삭제/ 검색의 연산도 최악의 경우 O(log n)의 속도를 제공

세부 특징**

• 각 노드는 1개의 키, 좌/우 자식, 그리고 부모노드의 주소를 저장한다.
• 자식노드가 없는 경우 NIL노드 라고 부르는 특수한 노드가 있다 가정한다.
• 따라서 모든 리프노드는 NIL 노드이며, 루트의 부모도 NIL노드라고 가정.
• 각 노드는 red or black 이다.
• 루트와 리프 노드는 항상 black이고, red 노드의 자식은 모두 black이다.
• 루트에서 NIL까지 향하는 모든 경로의 black 노드의 개수는 같다.

3. 레드블랙 트리의 높이

• 노드 X의 높이는 자신으로부터 리프노드까지의 가장 긴 경로에 포함된 엣지의 개수이다.
• 노드 X의 블랙-높이 bh(x)는 경로상의 블랙 노드 개수이다.
• 높이가 h인 경우, 블랙-높이는 >= h/2 이다.
• 노드 x의 루트로하는 임의의 서브트리는 적어도 2^bh(x) -1개의 내부노드를 포함한다
• n개의 내부 노드를 가지는 레드블랙트리의 높이는 2log2^(n+1)이하이다.

4. Left & Right Rotation

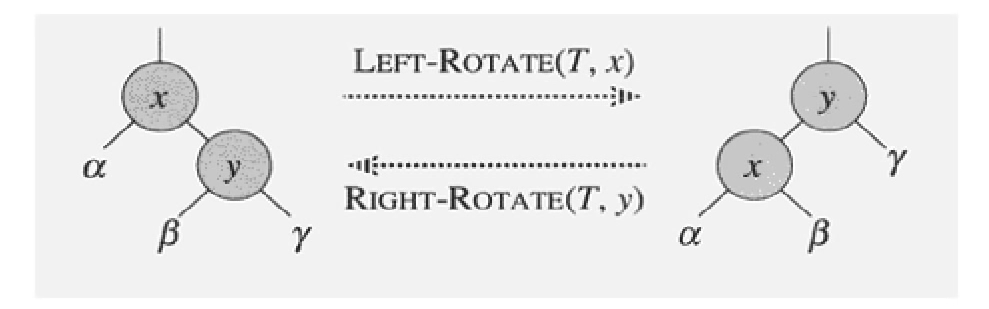
• Left Rotation Pseudo Code ( 필수 조건: right[x] != null )
  

  3 : y의 왼쪽의 부모를 x로 지정.
  4 : x의 부모를 y의 부모로 지정
  5 : x의 부모가 null 노드라면 ( = x == root )
  6 : y의 부모가 root[t]로 지정