백준 1707번 이분그래프 (python)

0. 문제

그래프의 정점의 집합을 둘로 분할하여, 각 집합에 속한 정점끼리는 서로 인접하지 않도록 분할할 수 있을 때, 그러한 그래프를 특별히 이분 그래프 (Bipartite Graph) 라 부른다.

그래프가 입력으로 주어졌을 때, 이 그래프가 이분 그래프인지 아닌지 판별하는 프로그램을 작성하시오.

• 입력
  입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V와 간선의 개수 E가 빈 칸을 사이에 두고 순서대로 주어진다. 각 정점에는 1부터 V까지 차례로 번호가 붙어 있다. 이어서 둘째 줄부터 E개의 줄에 걸쳐 간선에 대한 정보가 주어지는데, 각 줄에 인접한 두 정점의 번호 u, v (u ≠ v)가 빈 칸을 사이에 두고 주어진다.

• 출력
  K개의 줄에 걸쳐 입력으로 주어진 그래프가 이분 그래프이면 YES, 아니면 NO를 순서대로 출력한다.

• 제한
  2 ≤ K ≤ 5
  1 ≤ V ≤ 20,000
  1 ≤ E ≤ 200,000

• 예제 입력 1

2
3 2
1 3
2 3
4 4
1 2
2 3
3 4
4 2

예제 이해를 위한 그래프

예제 출력 1

YES
NO

1. 정답

1) 아이디어

예제입력을 그리면 다음과 같다.

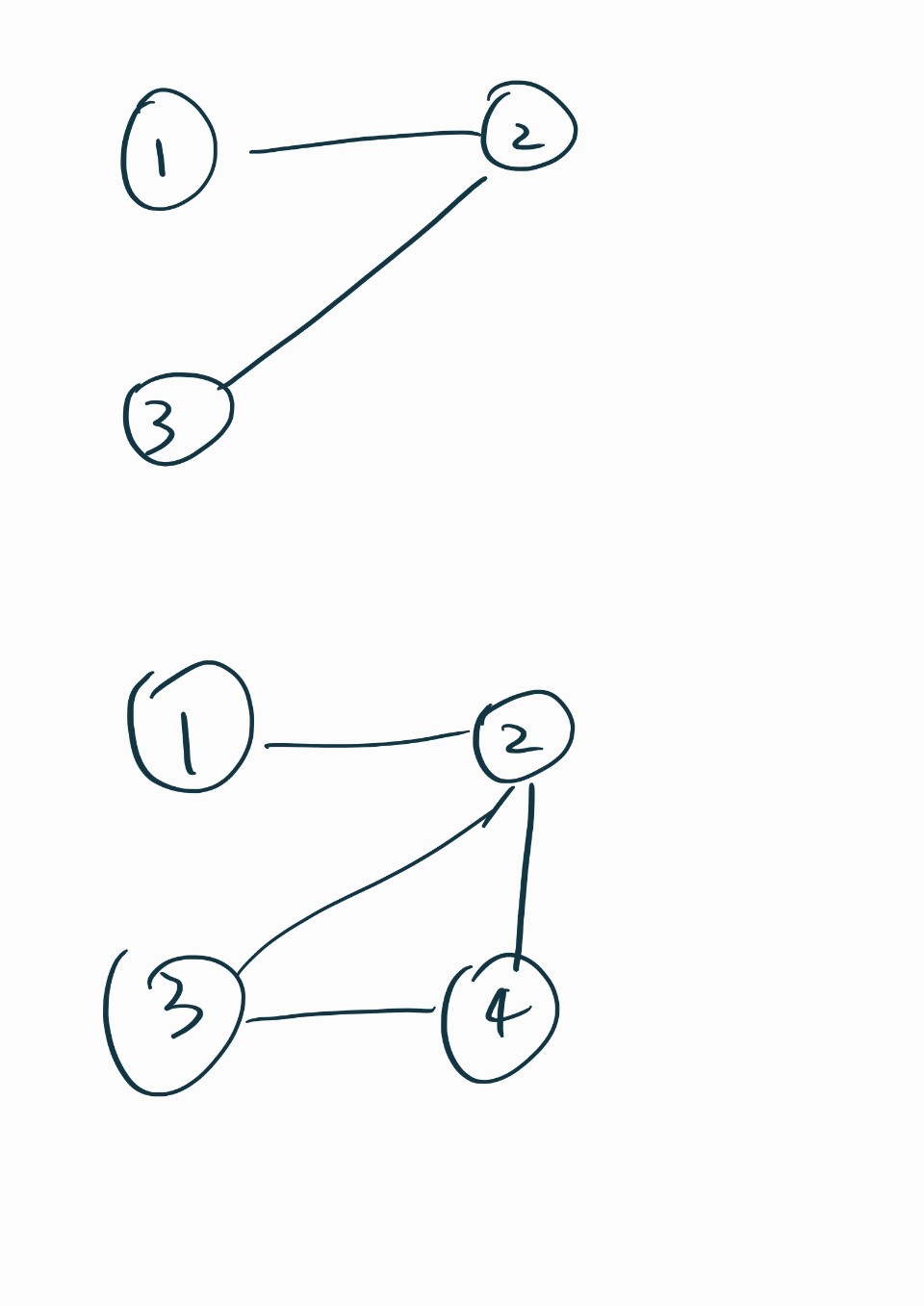
DFS를 수행하며 각 정점을 방문할 때마다 그 정점에 색을 칠하고, 그 정점과 연결된 모든 정점들을 서로 다른 색으로 칠한다. 만약 인접한 두 정점이 같은 색으로 칠해져 있다면, 그래프는 이분그래프가 아니다.

이분그래프는 정점들을 두개의 그룹으로 나눌 수 있으며, 각 그룹 내의 정점들 끼리는 서로 인접해 있지 않은 그래프를 의미. 다시말해, 이분 그래프는 모든 간선이 두 다른 그룹의 정점을 연결한다. 이러한 특성을 이용하여, 그래프의 모든 정점을 두 가지 색으로만 색칠할 수 있다.

이분 그래프의 예를 하나 들자면 정점들을 두 색상으로 칠할 수 있고, 같은 색상의 정점끼리는 직접 연결되지 않을 경우, 그 그래프를 이분 그래프로 간주한다

• 한 마디로 모든 정점을 두가지 색깔로 색칠할 때 간선으로 연결된 노드가 같은 색깔이면 안된다는 말이다.

2) 런타임 에러

def isBipartite(graph, v, color):
    for i in graph[v]: 
        if color[i] == 0:
            color[i] = -color[v]
            if not isBipartite(graph, i, color):
                return False
        elif color[i] == color[v]:
            return False
    return True

K = int(input())
for _ in range(K):
    V, E = map(int, input().split())
    graph = [[] for _ in range(V + 1)]
    color = [0] * (V + 1)  # 각 정점의 색을 저장하는 배열 (0: 아직 칠하지 않음, 1: 색1, -1: 색2)

    for _ in range(E):
        u, v = map(int, input().split())
        graph[u].append(v)
        graph[v].append(u)

    bipartite = True
    for v in range(1, V + 1):
        if color[v] == 0:
            color[v] = 1
            if not isBipartite(graph, v, color):
                bipartite = False
                break

    print("YES" if bipartite else "NO")

3) 해결방안

• 비재귀 방식으로 변경, python에서 재귀호출은 제한된다.
• 입력 처리 최적화: input()은 갔다버리자 초보자용이다. sys.stdin.readline()을 사용하여 입력을 더 빠르게 처리할 수 있다.

4) 정답

import sys
from collections import deque


def isBipartite(graph, start, color):
    queue = deque([start]) # 시작 정점으로 큐를 초기화
    color[start] = 1 # 색상 1로 색칠

    while queue: # 큐가 빌때까지 처리
        v = queue.popleft() # 다음 정점을 꺼냄
        for i in graph[v]: # 모든 인접 정점을 확인
            if color[i] == 0: #  정점이 색칠되지 않았다면
                color[i] = -color[v] # 반대 색상으로 색칠
                queue.append(i) # 추가 처리를 위한 큐 삽입
            elif color[i] == color[v]: # 인접 정점이 같은 색이라면 
                return False
    return True

input = sys.stdin.readline
K = int(input())
for _ in range(K):
    V, E = map(int, input().split())
    graph = [[] for _ in range(V + 1)]
    color = [0] * (V + 1)

    for _ in range(E):
        u, v = map(int, input().split())
        graph[u].append(v)
        graph[v].append(u)

    bipartite = True
    for v in range(1, V + 1):
        if color[v] == 0:
            if not isBipartite(graph, v, color):
                bipartite = False
                break

    print("YES" if bipartite else "NO")