SKN - Week04

SK Networks Family AI Camp 4기
4주차 24.08.26 - 24.08.30

---

📢 IntroDuction

SK Networks Family AI Camp 4기에서 4주차 배운 것을 기록합니다.

---

240836_day15

Numpy

• 배열 생성
• 배열 조작
• 배열 탐색
• 배열 연산
• 통계 함수

240827_day16

Pandas

• Series : 1D 행렬에 index가 존재
• DataFrame : 2D 행렬에 index & column 존재 (여러 series의 합)
• 시계열 데이터

240828_day17

Visualization

• 데이터 전체를 스케일링 하지 말고 나눠서 한다.
• Matplotlib
  : Python 언어 및 NumPy 라이브러리를 활용한 ploting 라이브러리
• Seaborn : Matplotlib을 기반으로 하는 Python 데이터 시각화 라이브러리
• Plotly: 차트 유형을 지원하는 대화형 오픈 소스 ploting 라이브러리

240829_day18

Scaling : data의 scale을 이치시키는 작업

1. Normalization (정규화)

• feature의 최솟값 0, 최댓값 1로 스케일
  $X_i^{\prime} = \frac {X_i-X_{min}}{X_{max} - X_{min}}$

• sklearn의 MinMaxScaler 사용

# fit을 사용하지 않은 scaler를 사용할 수 없다
# 데이터를 표준화시키는 방법을 학습하는 것과 동시에 주어진 데이터 표준화

min_max_scaler = MinMaxScaler()
min_max_scaler = min_max_scaler.fit_transform()

2. Standardization (표준화)

• feature의 평균 0, 분산 1로 스케일 (즉, 데이터의 분포를 표준정규분포로 생성)
  $X_i^{\prime} = \frac {X_i - \mu}{\sigma}$

• sklearn의 StandardScaler 사용

standard_scaler = StandardScaler()
standard_scaler = = standard_scaler.fit_transform()

3. Robust Scaling

• 평균과 분산 대신 중간값과 사분위값을 사용하여 스케일링

  • 중간값: 데이터 정렬 후 중간에 있는 값

  • 사분위값: 데이터 정렬 후 1/4, 3/4에 위치한 값

    $X_i^{\prime} = \frac {X_i - X_{median}}{Q_3 - Q_1}$

• 이상치에 대한 영향력 감소
  (극단치의 영향을 받지 않도록 µ를 빼지 않고 median을 뺀다)

• sklearn의 RobustScaler 사용

robust_scaler = RobustScaler()
robust_scaler = robust_scaler.fit_transforma()

240830_day19

Dimensionality_reduction

Dimensionality Reduction

• feature가 많아지면 feature들 간의 관계 파악이 어려워 차원 축소를 통하여 이를 해결

• 차원의 저주: 데이터 학습을 위해 차원이 증가하면서 학습 데이터 수가 차원의 수보다 적어져 성능 저하

• LDA(Linear Discriminant Analysis)
  
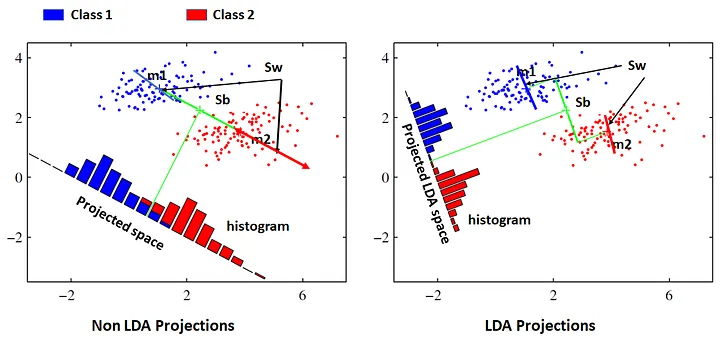
  : 입력된 데이터를 저차원 공간으로 projection하여 차원 축소(지도학습에서 사용)

• PCA(Principal Component Analysis)
  : 데이터 분산을 최대화할 수 있는 eigen vector로 projection

---

t-SNE
: t-distributed Stochastic Neighbor Embedding)
1. 데이터 포인트 간의 유사도 계산
2. 저차원에서 유사도 계산
3. 저차원과 고차원의 유사도 분포 근사

• Manifold
  : 데이터가 존재하는 공간으로 말려있는 roll을 풀면 저차원의 manifold로 표현 가능
  

---

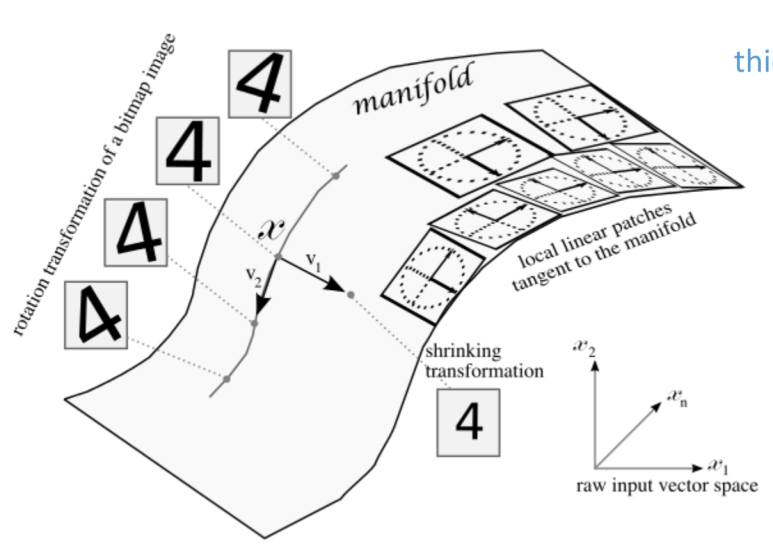
UMAP
: 데이터의 위상 관계를 이용하여 저차원으로 매핑

• metric 기반 데이터마다 가까운 neighbor 찾아