[백준/c언어] 1712번 손익분기점

EOH·2023년 2월 14일

백준

목록 보기

1/5

문제

월드전자는 노트북을 제조하고 판매하는 회사이다. 노트북 판매 대수에 상관없이 매년 임대료, 재산세, 보험료, 급여 등 A만원의 고정 비용이 들며, 한 대의 노트북을 생산하는 데에는 재료비와 인건비 등 총 B만원의 가변 비용이 든다고 한다.
예를 들어 A=1,000, B=70이라고 하자. 이 경우 노트북을 한 대 생산하는 데는 총 1,070만원이 들며, 열 대 생산하는 데는 총 1,700만원이 든다.
노트북 가격이 C만원으로 책정되었다고 한다. 일반적으로 생산 대수를 늘려 가다 보면 어느 순간 총 수입(판매비용)이 총 비용(=고정비용+가변비용)보다 많아지게 된다. 최초로 총 수입이 총 비용보다 많아져 이익이 발생하는 지점을 손익분기점(BREAK-EVEN POINT)이라고 한다.
A, B, C가 주어졌을 때, 손익분기점을 구하는 프로그램을 작성하시오.

입력

첫째 줄에 A, B, C가 빈 칸을 사이에 두고 순서대로 주어진다. A, B, C는 21억 이하의 자연수이다.

출력

첫 번째 줄에 손익분기점 즉 최초로 이익이 발생하는 판매량을 출력한다. 손익분기점이 존재하지 않으면 -1을 출력한다.

문제 링크

설명

시간복잡도를 해결하는 문제이다.
처음에는 while문 무한루프를 이용해 n이 1일 때부터 손익분기점이 될 때까지 반복문을 돌렸다. 그러다보니 예제에 나와있는 고정비용이 21억일 때는 21억번 이상 반복해야 정답을 찾을 수 있어 굉장히 비효율적이었다.

처음 생각했던 코드

#include <stdio.h>

int validator (int a, int b, int c)
{
	int x, y;

	x = (c * 1) - (a + (b * 1));
	y = (c * 2) - (a + (b * 2));

	if (x >= y)
		return (-1);
	return (1);
}

int bep_finder(int a, int b, int c)
{
	int profit, spending, bep;
	int n;

	n = 1;
	while (1)
	{
		profit = c * n;
		spending = a + (b * n);
		if (profit - spending > 0)
		{
			bep = n;
			break;
		}
		n++;
	}
	return (n);

}

int main(void)
{
	int a, b, c;
	int bep;

	scanf("%d %d %d", &a, &b, &c);

	if(validator(a, b, c) == -1)
	{
		printf("-1");
		return (0);
	}
	bep = bep_finder(a, b, c);
	printf("%d", bep);

	return (0);
}

정답 코드

#include <stdio.h>

int main()
{
	int a, b, c;
	int bep;

	scanf("%d %d %d", &a, &b, &c);
	if (c - b <= 0)
	{
		printf("-1");
		return (0);
	}
	bep = (a / (c - b)) + 1;
	printf("%d", bep);
	return (0);
}

항을 이항하는 것만으로 시간복잡도가 해결되는 경우가 있다.
이번 문제도 처음에 세웠던 식에서 항을 이항하여 바로 손익분기점을 넘기는 물건판매량을 구할 수 있었다.

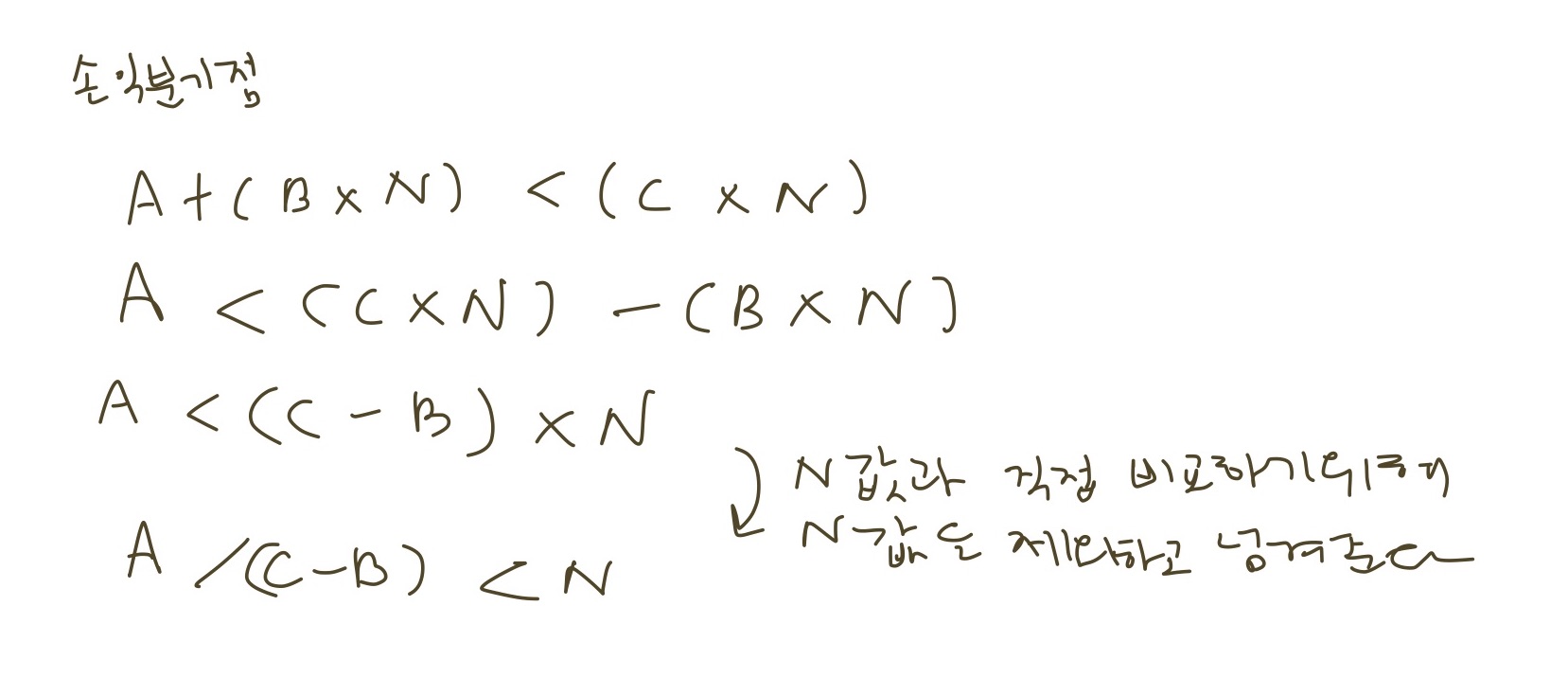
위 식처럼 A/(C-B) 는 손익분기점을 넘기 직전의 N값이 되며 손익분기점을 넘는 N값은 (A/(C-B)) + 1이 된다.