해시

🌈Hash 자료구조가 나온 배경

---

💡배열

원소 하나를 저장하고 검색하는데 평균 O(n)의 시간 소요

• 자료의 개수와 비례하는 시간이 걸리게 됨
• 효율적으로 자료를 저장할 수 있는 방법이 없을까?

💡트리

원소 하나를 저장하고 검색하는데 평균 O(logn)의 시간 소요

저장된 자료의 양에 상관없이 원소 하나를 저장하고 검색하는 것을 상수 시간에 가능하게 할 수는 없을까? 라는 질문에서 나오게 된것이 해시 테이블이다.

🌈해시테이블

---

• (Key, Value)로 데이터를 저장하는 자료구조 중 하나
• 빠르게 데이터를 검색할 수 있음
• 평균 시간 복잡도 O(1)

💡해시 테이블이 빠른 검색속도를 제공하는 이유는❓

해시 테이블은 각각의 Key값에 해시 함수를 적용해 배열의 고유한 index를 생성하고, 이 index를 활용해 값을 저장하거나 검색하기 때문이다. 여기서 실제 값이 저장되는 장소를 버킷 또는 슬롯이라고 한다.

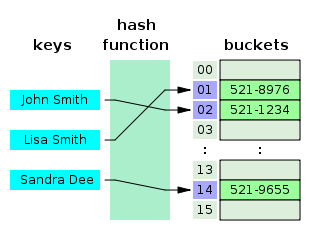
예를 들어, (key, value)가 (”John smith”, “521-1234”)인 데이터를 크기가 16인 해시 테이블에 저장한다고 하면,

1. index = hash_function(”John Smith”)%16 해시 함수 연산을 통해 해시 값을 계산
2. 이 해시 값을 주소로 하는 위치에 array[index] = “521-1234”로 전화번호를 저장

이러한 구조로 데이터를 저장하면, 저장 후에 검색을 할 때도 원소의 해시값을 계산해 바로 해당 위치로 이동하므로 빠르게 데이터를 저장/삭제/조회 가능하고, 평균 시간복잡도가 O(1)이 된다.

❗ 배열과 트리는 검색할 때, 기존에 저장된 자료와 원소 하나하나를 비교해야 하지만, 해시 테이블은 기존에 저장된 자료와 비교할 필요 없이 해시함수를 통해 접근 가능하기 때문에 굉장히 빠른 시간 내에 계산할 수 있음

💡해시 함수

• 임의의 길이의 데이터를 고정된 길이의 데이터로 매핑하는 함수
• 종류
  1. Division Method
  2. Digit Folding
  3. Multiplication Method
  4. Univeral Hashing
• 좋은 해시 함수의 조건
  • 계산이 간단해야 한다.
  • 입력 원소가 해시 테이블 전체에 고루 저장되어 있어야 한다.
• 해시 함수의 특징
  • 같은 입력값에 대해 같은 출력 값이 보장
  • 서로 다른 입력 값으로부터 동일한 출력값이 나올 가능성이 희박하므로, 입력값에 대한 무결성이 보장됨
  • 일방향성을 가짐 (해시값을 이용해 원래의 값을 찾을 수는 없기 때문)

해시 테이블 전체에 고루 저장되어야 하는 이유는 해시 테이블 한 곳에 원소가 모이게 되면 해시 충돌이 일어날 수 있기 때문이다.

💡해시 충돌

• 해시 함수가 서로 다른 두 개의 입력값에 대해 같은 출력값을 내는 상황

🌈해시 충돌 해결

---

1. 체이닝(chaining)

• 같은 주소로 해싱 되는 원소를 모두 하나의 연결 리스트에 매달아서 관리함
• 원소를 검색할 때는 해당 연결 리스트의 원소들을 차례로 지나가면서 탐색함

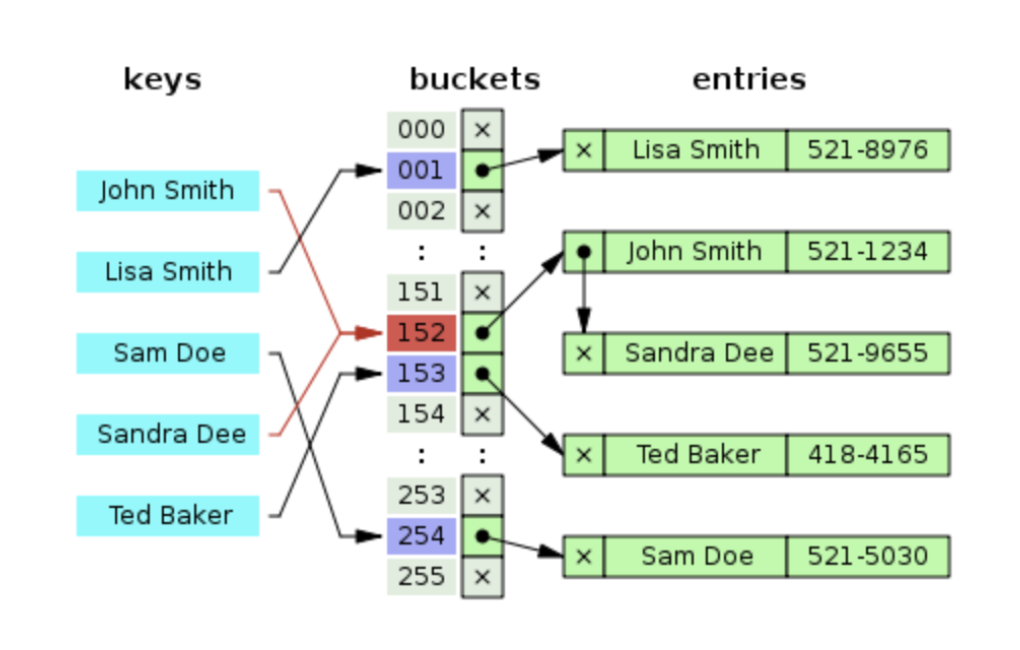
• 장점: 해시 테이블의 확장이 필요 없고, 간단하게 구현 가능
• 단점: 해당 방법은 데이터의 수가 많아지면 동일한 버킷에 chaining되는 데이터가 많아지며 그에 다라 캐시의 효율성이 감소한다.

2. 개방 주소법(Open Addressing)

• 체이닝과 달리 어떻게든 주어진 테이블 공간에서 해결
• 따라서 모든 원소가 반드시 자신의 해시 값과 일치하는 주소에 저장된다는 보장이 없음

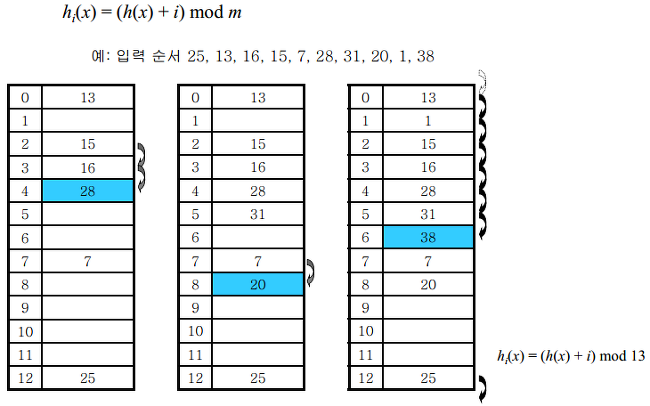
1. 선형조사(linear probing)

• 가장 간단한 충돌 해결 방법
• 충돌이 일어난 자리에서 i에 관한 일차 함수의 보폭(고정폭)으로 점프해 비어 있는 버킷에 데이터를 저장
• 테이블의 경계를 넘어갈 경우에는 맨 앞으로 돌아감
• 이 방법의 경우, 비어있는 버킷의 수가 많이 없으면, 빈 버킷을 찾는 연산의 횟수가 증가하여 비효율적임

2. 이차원조사(quadratic probing)

• 바로 뒷자리를 보는 대신 보폭을 이차 함수로 넓혀가면서 본다
• 예를 들어, i번째 해시 함수를 h(x)에서 i의 제곱만큼 떨어진 자리로 삼는다
  • 예를 들어 처음 충돌이 발생한 경우에는 1만큼 이동하고 그 다음 계속 충돌이 발생하면 2^2, 3^2 칸씩 옮기는 방식
• 특정 영역에 원소가 몰려도 그 영역을 빨리 벗어날 수 있다는 장점이 있음
• 단점: 최초 해시 값이 같은 원소의 경우, 다른 원소 루트를 그대로 따라가기 때문에 빈 버킷을 찾는데 연산의 횟수가 많아짐

3. 더블 해싱(double hasing)

• 두 개의 함수를 사용
• 하나의 함수는 최초의 해시 값을 얻을 때, 다른 하나의 함수는 해시 충돌이 일어났을 때 이동할 폭을 얻을 때 사용
• 두 원소의 첫 번째 해시값이 같더라도 두 번째 해시 값까지 같을 확률은 매우 작으므로 서로 다른 보폭으로 점프를 하게 됨

(참고) https://velog.io/@syoung125/해시테이블이란