1. 정렬 알고리즘이란
🌻개념
특정 원소들을 번호순이나 사전 순서와 같이 일정한 순서대로 열거하는 알고리즘
🌻정렬 알고리즘은 왜 중요한가?
- 컴퓨터 분야에서 중요시되는 문제 중 하나 이며, 탐색에 용이함.
- 프로그래밍과 알고리즘 이해에 많은 도움이 됨 → 프로그래밍 기초 문법인 for문 if문, 분할 정복 알고리즘, 자료구조, 시간 복잡도
2. 정렬 알고리즘 종류
🌻 버블 정렬
- 가장 기초적인 알고리즘.
- 인접한 두개의 요소를 비교해가면서 큰 숫자를 오른쪽으로 스왑하며 정렬된다.
- 시간복잡도는 Best는O(n) 평균 O(n^2) 최악 O(n^2)
🔆구현 코드
- 탐색범위
- Outer: 0→ n-1
- 마지막 element는 이미 비교 되어서 n-1번째까지 반복
- Inner: 0 → n-i-1
- Outer 루프가 한번 돌때 마다 element 하나의 최종위치가 확정되므로 이미 정렬된 부분 제외하기 위해 n-i-1까지 반복
- Outer: 0→ n-1
private static void bubbleSort(int[] nums){ // 3 4 1 5 2
int size = nums.length;
for(int i=0; i<size-1; i++){ //Outer 루프: 전체 요소를 반복
for(int j=0; j<size-i-1; j++){ //Inner 루프: 그 안에서 정렬을 해야하는 요소를 반복
if(nums[j]>nums[j+1]){//두 개의 요소 비교를 통해 왼쪽에 있는 값이 더 큰지 확인하고 더 크면 스왑
swap(nums, j, j+1);
}
}
}
}
- 장점: 구현이 매우 간단함
- 단점: 순서에 맞지 않는 요소들의 교환이 자주 일어난다.
🌻 선택 정렬
- 가장 기초적인 알고리즘
- 전체 범위에서 차례대로 가장 작은 숫자를 탐색하고, 가장 왼쪽부터 차례대로 교환하는 방식
- 장점: 자료 이동 횟수가 미리 결정된다.
- 단점: 값이 같은 요소가 있다면 상대적인 위치가 변경될 수 있다.
- 시간복잡도: 매번 전체요소를 한번씩 돌기 때문에 (최악, 최선, 평균): O(n^2)
🔆구현 코드
private static void selectionSort(int[] nums){// 3 4 1 5 2
int size = nums.length;
for(int i=0; i<size-1; i++){//전체 범위 반복
int minIdx = i; //최솟값을 담을 인덱스 생성
for (int j=i+1; j<size; j++){
if(nums[j]<nums[minIdx]){ //반복과정에서 최솟값을 찾음
minIdx = j;
}
}
swap(nums, i, minIdx); //찾은 최솟값을 왼쪽으로 교환
}
}
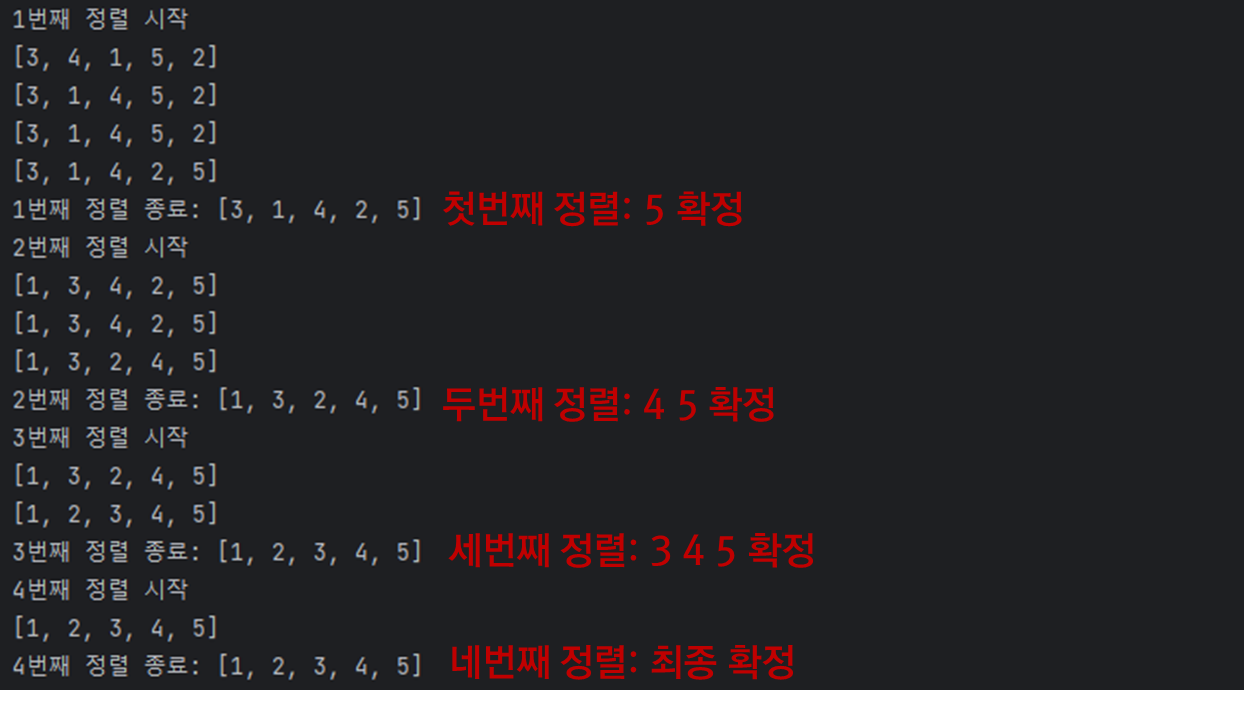
🌻 삽입 정렬
- 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여, 자신의 위치를 찾아 삽입하는 방식
- 이미 정렬된 배열에서 자기 자신의 위치를 찾아 삽입된다고 하여 삽입 정렬이라고 함.
private static void insertSort(int[] nums){
int size = nums.length;
for(int i=1; i<size; i++){ //전체 범위 반복
System.out.println((i) + "번째 정렬 시작");
int current = nums[i]; //아직 정렬되지 않은 배열에서 삽입될 i번째 숫자를 현재 변수에 저장
int tobeInsertedIdx = i-1; //정렬된 부분에서 삽입할 위치 인덱스도 저장
while(tobeInsertedIdx>=0 && nums[tobeInsertedIdx] > current){ //정렬된 부분에서 i번째 숫자가 삽입될 위치를 탐색
nums[tobeInsertedIdx+1] = nums[tobeInsertedIdx];
tobeInsertedIdx--; //삽입할 위치 인덱스 1 감소
}
nums[tobeInsertedIdx+1] = current;
System.out.println((i) + "번째 정렬 종료: "+ Arrays.toString(nums));
}
}
🌻 병합 정렬
- 복잡하지만 호율적인 알고리즘
- ‘분할 정복’이라는 알고리즘 디자인 기법에 근거하여 복잡한 문제를 복잡하지 않은 문제로 ‘분할’하여 ‘정복’하는 방식
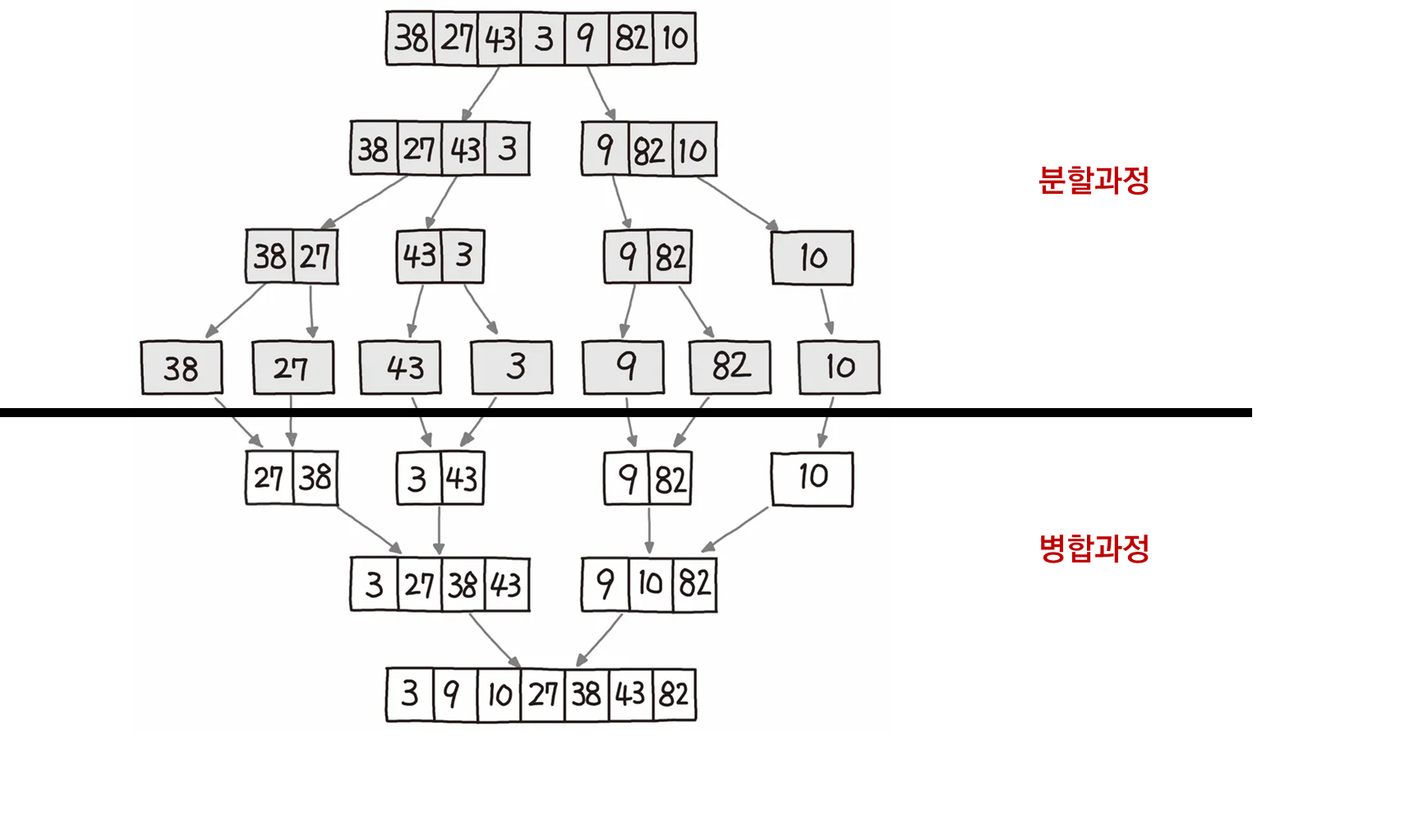
- 분할과정
- 정렬이 되지 않는 숫자를 가운데 값을 기준으로 분리. 더이상 분해가 될 수 없을 때까지 분리함
- 병합과정
- 모두 분리되었을 때, 각 요소를 비교하여 병합하는 방식
🔆구현 코드
public static void mergeSort(int[] nums, int first, int last){
if(first < last){ //분할된 요소가 하나 이상인지 확인
//중간 값
int mid = (first + last) / 2;
//분할
mergeSort(nums, first, mid);
mergeSort(nums, mid+1, last);
//병합
mergeTwoArea(nums, first, mid, last);
}
}
private static void mergeTwoArea(int[] nums, int first, int mid, int last){
int leftIdx = first; //첫번째 영역에서의 첫번째 인덱스
int rightIdx = mid +1; //두번째 영역에서의 첫번째 인덱스
int[] sortedArray = new int[last+1]; //병합한 결과를 담을 배열
int sortIdx = first; //병합 한 결과를 담을 배열의 인덱스
//병합할 두 영역의 데이터들을 비교
while(leftIdx<=mid && rightIdx <= last){
if(nums[leftIdx]<=nums[rightIdx]){//첫번째 영역의 값이 더 작은 경우
sortedArray[sortIdx] = nums[leftIdx];
leftIdx++;
}else{//두번째 영역의 값이 더 작은 경우
sortedArray[sortIdx] = nums[rightIdx];
rightIdx++;
}
sortIdx++;
}
//비교 후 두 영역 중 남은 숫자 대입
if(leftIdx > mid){ //배열의 앞부분이 모두 sortedArray에 옮겨졌다면
for(int i = rightIdx; i<=last; i++){
sortedArray[sortIdx] = nums[i];
sortIdx++;
}
}else{ //배열의 뒷부분이 모두 sortedArray에 옮겨졌다면
for(int i=leftIdx; i<=mid; i++){
sortedArray[sortIdx] = nums[i];
sortIdx++;
}
}
//정렬된 결과를 담은 배열에서 원래 배열로 복사
for(int i =first; i<=last; i++){
nums[i] = sortedArray[i];
}
}- 장점: 데이터 분포의 영향을 덜 받는다. 퀵 정렬과는 달리 기준값을 설정하는 과정 없이 중간값을 둠으로써 입력값에 상관없이 정렬시간은 같음
- 단점: 요소를 배열로 구성하면, 임시 배열이 필요하므로 정렬을 위한 추가 메모리 필요
- 시간복잡도: (최선, 평균, 최악): O(nlogn)
🌻 퀵정렬
- 복잡하지만 효율적인 알고리즘으로 실제로 가장 많이 사용됨
- 특정 요소를 기준점으로(pivot)으로 잡고, 기준점보다 작은 요소는 왼쪽, 기준점보다 큰 요소는 오른쪽으로 두고, 왼쪽과 오른쪽을 각각 정복하는 방식
- 다른 알고리즘보다 효율적이고 빠름
🔆 정렬과정
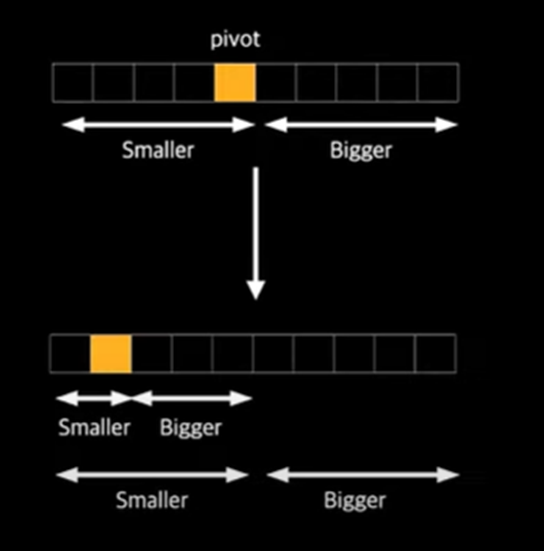
먼저 pivot을 설정함(pivot을 설정하는 기준은 다양함)
pivot을 기준으로 왼쪽엔 작은 값, 오른쪽엔 큰 값이 정렬되게 한다.
정렬이되면 각각 왼쪽과 오른쪽을 분할하여 각각 부분에서 다시 퀵 정렬을 사용하게 됨
🔆구현 코드
private static void quickSort(int[] nums, int first, int last){
if(first<last){
int pivot = partition(nums, first, last);
quickSort(nums, first, pivot-1); //왼쪽 영역 정렬
quickSort(nums, pivot+1, last); //오른쪽 영역 정렬
}
}
private static int partition(int[] nums, int first, int last){
int pivot = nums[first]; //피벗의 위치 (가장 왼쪽으로 설정)
int low = first + 1;
int high = last;
//교차되지 않을 때까지 반복
while(low<=high){
//피벗보다 큰 값을 찾는 과정
while(pivot > nums[low] && low <= last){
low++;
}
//피벗보다 작은 값을 찾는 과정
while (pivot < nums[high] && high >= (first + 1)) {
high--;
}
//교차되지 않은 상태라면 swap
if(low <= high){
swap(nums, low, high);
}
}
swap(nums, first, high); //피벗과 high가 가리키는 대상 swap
return high; //옮겨진 피벗의 위치정보 반환 (정렬이 완료된 인덱스 반환)
}- 장점: 평균 실행시간이 다른 알고리즘보다 빠른 편
- 단점: Pivot에 따라 성능차이가 심함
- 시간복잡도
- 퀵 정렬은 pivot이 중간에 가까운 값을 찾을 수록 성능이 좋음
- 최악: O(n^2)
- 평균: O(nlogn)
- 최선 O(nlogn)
어떤 정렬알고리즘을 써야하는가?
→ 시간복잡도가 전부는 아님! 알고리즘별로 각각 장단점이 있으므로 상황에 맞게 선택!
1. 안정성
- O : 버블, 삽입, 병합
- X : 선택, 퀵, 힙
2. 공간복잡도: 메모리 사용이 중요할 때
- 1 :버블, 삽입, 선택, 힙
- n : 병합
3. 지역성(Locality)
4. 키 값들의 분포 상태 등..
