[프로그래머스] Lv1 - 소수 찾기

문제

프로그래머스 연습문제

• Lv 1. 소수 찾기 (Python)
  https://school.programmers.co.kr/learn/courses/30/lessons/12921

코드 구현

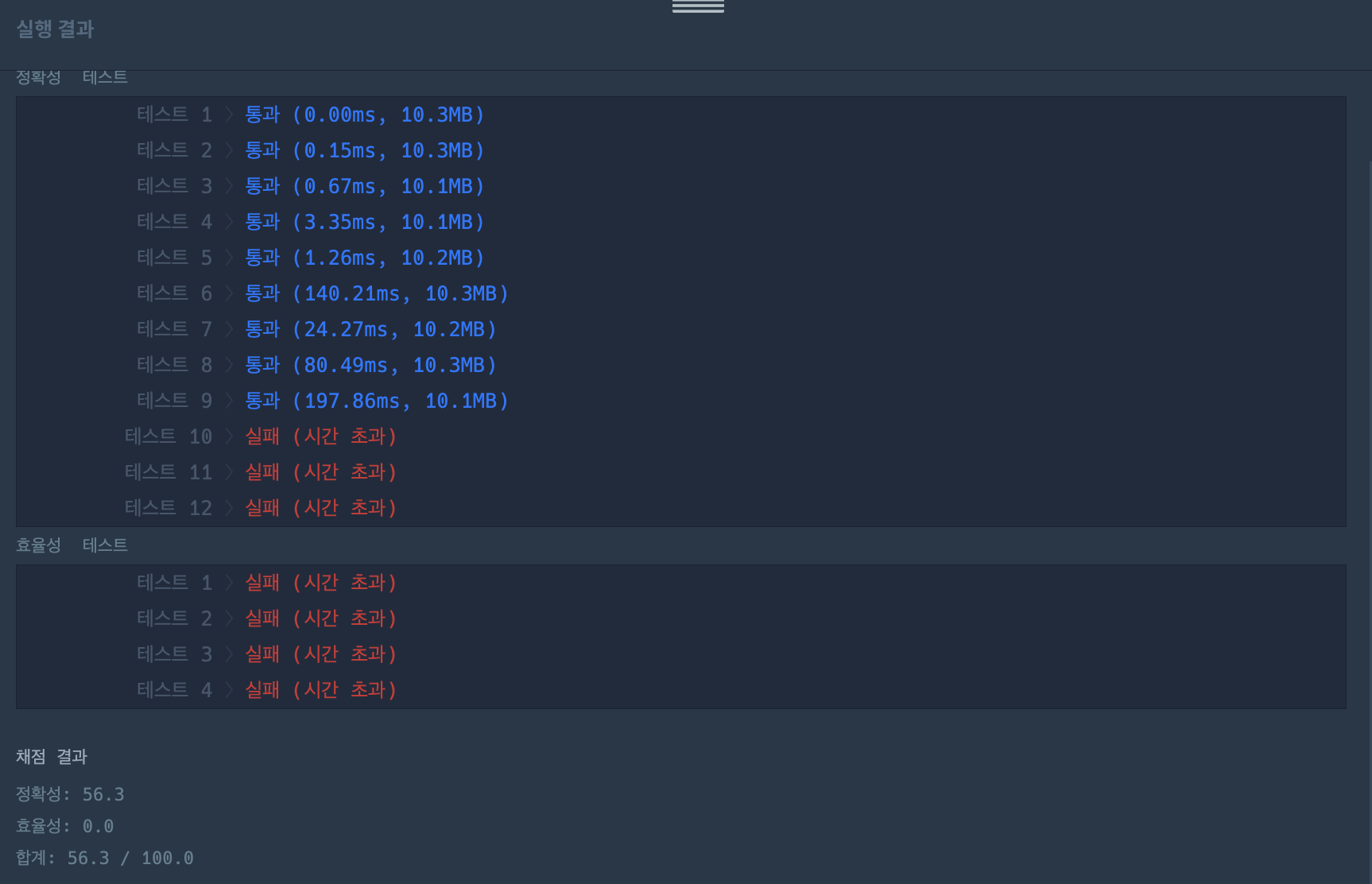
오답 코드 (시간 초과)

def solution(n):
    answer = 0

    sosu = list()

    for i in range(1, n + 1):
        check_sosu = True
        for j in range(2, (i//2)+1):
            if (j != i and i % j == 0):
                check_sosu = False
                break
        if (i != 1 and check_sosu):
            sosu.append(i)
            
    answer = len(sosu)

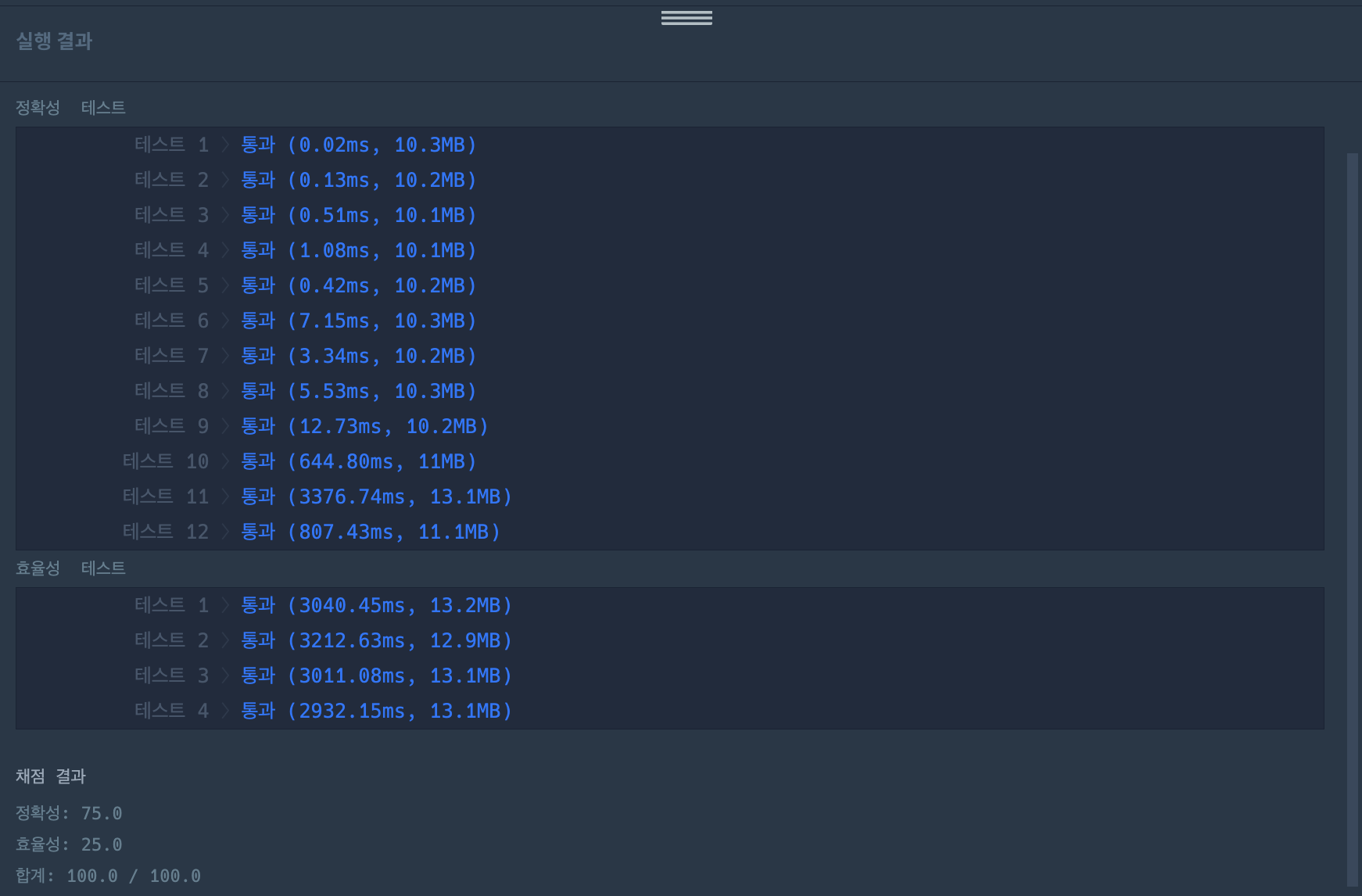
    return answer

수정 코드 (테스트는 통과)

def solution(n):
    answer = 0

    sosu = list()

    for i in range(2, n + 1):
        check_sosu = True
        for j in range(2, int(i ** (1 / 2)) + 1):
            if (i % j == 0):
                check_sosu = False
                break
        if(check_sosu):
            sosu.append(i)
            
    answer = len(sosu)

    return answer

개선 코드 → 에라토스테너스의 체 사용

def solution(n):
    answer = 0

    prime_nums = list()

    a = [0, 0] + [1] * (n - 1)  # 0부터 n까지 소수판별을 위해 사용할 리스트 (0과 1은 소수에서 제외되므로 0으로 설정, 2부터 n까지는 1로 설정)

    for i in range(2, n + 1):
        if (a[i] == 1):  # 1을 만나면 -> 소수
            # prime_nums.append(i)
            answer += 1
            for j in range(2 * i, n + 1, i):  # i가 소수면 -> i의 배수들은 소수에서 제외됨 (약수로 i를 갖기 때문에)
                a[j] = 0  # i의 배수들을 0으로 설정 (소수 X)

    return answer

풀이

오답 코드 (시간 초과)

• 소수를 찾는건 2부터 n까지의 수를 하나하나 나눠봤을 때, 자기자신을 제외하고 나눠지는 수가 존재하면 (== 1과 자기자신을 제외한 약수가 존재한다면) → 소수가 아님
  이기 때문에 간단하게 약수들은 안에서 짝이 있기 때문에 절반으로 나누어서 해당 범위까지 돌았을 때 만약 나눠지는 수가 있다면 소수가 아닌 것으로 코드르 짰다.
• 그러나 시간 초과가 발생하였다. 아무래도 더 효율성있게 짰어야 했다.
• 

수정 코드 (테스트는 통과)

• 이전에 약수 관련 문제에서 시간복잡도를 줄인 버전의 약수 구하기를 사용하였다.
  • https://velog.io/@ejung803/프로그래머스-Lv1-기사단원의-무기
• 테스트는 통과하였으나, 사실상 테스트 11번이 어어어엄청 오래 걸렸고 효율성 테스트 결과도 그렇게 좋지 않게 나왔다.
• 

개선 코드 → 에라토스테너스의 체 사용

• 정답을 살펴보니 에라토스테너스의 체를 사용해야 한다고 한다… (이게 뭐죠 처음 들어봐요 🤔)
  • 범위 내의 모든 소수를 구할 때 쓰는 알고리즘 ! 이렇게 많은 소수를 판별해야 할 때 써야한다.
• 에라토스테너스의 체는 우선 2부터 순서대로 살펴보는데, 만약 새로운 소수를 발견할 때마다 해당 소수의 배수들은 모두 소수가 아니라고 표시하며 걸러가는 알고리즘이다.
• [0, 0] + [1] * (n-1) 의 배열을 만들어서 판별한다.
  • 이는 각 인덱스가 숫자를 표현 / 0은 소수 X / 1은 소수 O
  • 우선 0과 1은 모두 소수가 아니므로 0으로 표기, 2부터 n까지는 우선 배수를 판별하기 전까지는 모두 소수로 해둔다.
    따라서 1로 표기한다.
• 2부터 시작한다면, 2는 소수이기 때문에 → 2의 배수들 (4, 6, 8, 10 …) 은 모두 소수가 아닌 0으로 변경한다.
• 3을 만나면, 3도 우선 소수이기 때문에 → 3의 배수들 (6, 9, 12, 15 …) 은 모두 소수가 아닌 0으로 변경한다.
• 4를 만났을 때, 4는 0이기 때문에 소수가 아니다. 따라서 건너뛴다. … (반복)
  
• 에라토스테너스의 체는 사실상 소수일 때만 반복문이 수행되기 때문에 효율성을 크게 높여준다.
  • 시간복잡도 : $O(n\log(\log {n}))$, 사실상 O(n)에 매우 근접한 시간 복잡도라고 한다 …!
• 

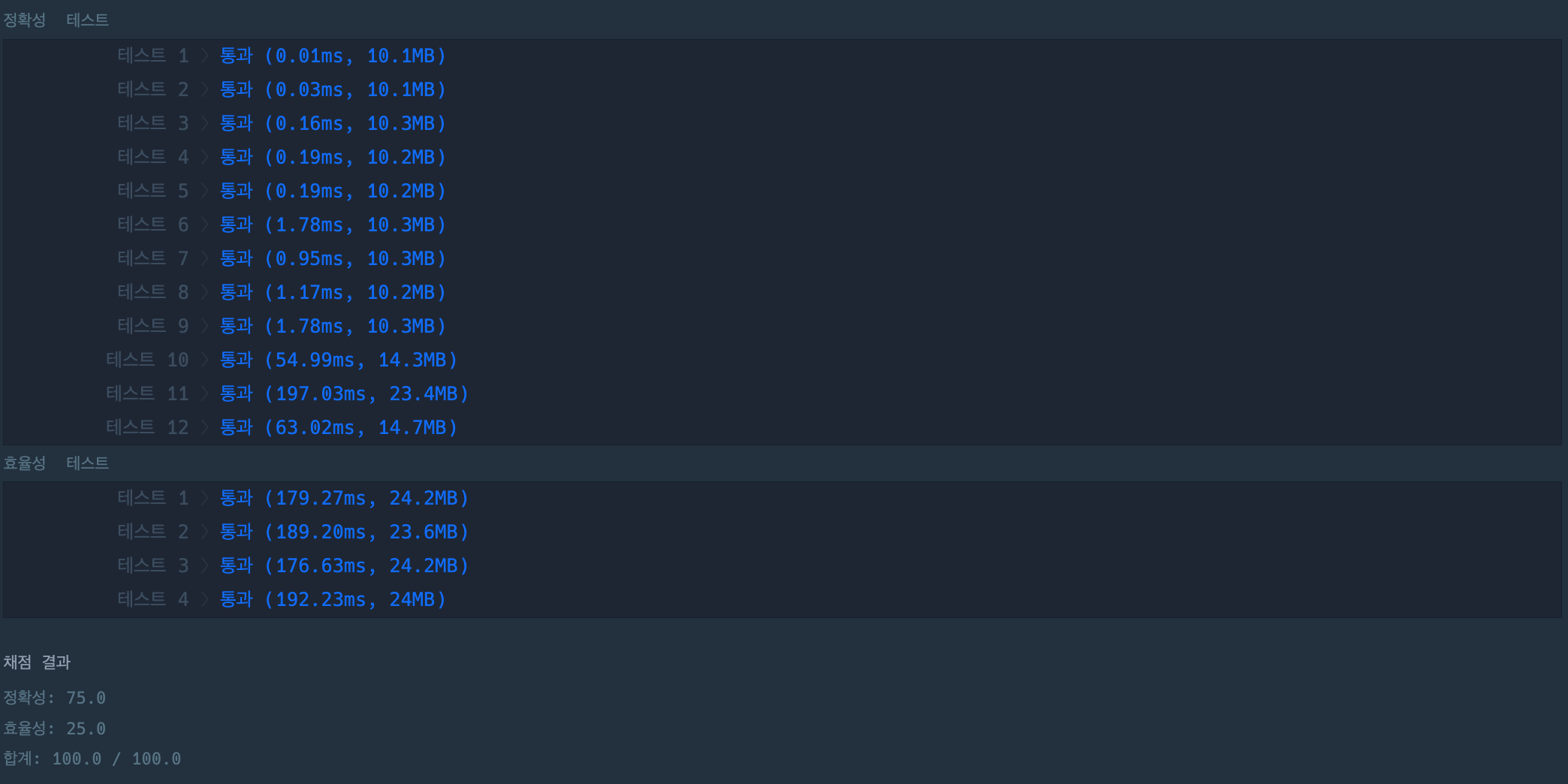
성능이 확실히 좋아졌다 !!!

참고1 : https://chanhuiseok.github.io/posts/algo-42/
참고2 : https://wikidocs.net/21638

What I learned

정답 코드 ) 2부터 n까지의 배열에서 배수를 찾으면 바로 한번에 제거하는 식

def solution(n):
    num=set(range(2,n+1))

    for i in range(2,n+1):
        if i in num:
            num-=set(range(2*i,n+1,i))
    return len(num)