내가 코딩테스트 문제를 풀면서 가장 많이(는 아니지만 자주 쓰는.. ㅎ) 쓰는 자료구조 set을 파헤쳐볼까 한다. 이유는 set이 효율적인 자료구조이고 방문 복잡도가 O(1)이기 때문에 그래프 bfs, dfs 알고리즘에서 visit을 확인할때 set을 사용하는 편이다. 그런데 언제부턴가 set을 남용하기 시작했고 어디에서인지도 모르는 곳에서 자꾸 시간초과가 뜨기 시작했다. 오늘은 set의 장점과 단점을 파헤치고 가겠다!
set(집합)
특징
- 순서가 없다.
- 모든 value가 unique하다.
- mutable한 객체이다.
- 집합의 내부 원소로 mutable한 값은 가질 수 없다.
( unique함이 포인트인데 안에 넣어놓고 바꾸면 말짱 도루묵이기 때문이 아닐까?)
mutable이란?
mutable 만 다뤄도 하나의 포스트가 생길 것 같지만 간단하게 요약하자면 변한다는 뜻이다.
이는 call by value , call by reference 와도 관계가 있지만 이번 포스트에서는 다루지 않겠다.
mutable한 자료구조에는 대표적으로 List와 Dict가 있다.
그의 반대를 immutable이라 부르는데 한번 선언하면 절대 변하지 않는다.
이게 안변한다고? 싶은 자료구조가 대부분인데 대표적으로 tuple, String 이 있다.
ps ) 궁금하다면 a에 선언후 b로 참조를 하고 b를 바꿔봐라 b를 바꿨을때 a가 바뀌면 mutable, 안바뀌면 immutable이다.
활용법은 다른 포스트를 찾아보시라! (혹시나해서... 선언만)
>>> s = set()
>>> type(s)
<class 'set'>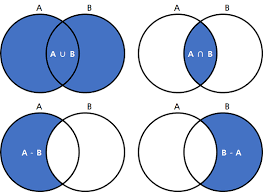
set은 위와 같은 집합구조를 쉽게 표현할 수 있는 가장 쉬운 자료구조 이다.
합집합은 A | B, 교집합은 A & B (union, intersection 등도 가능하지만 나는 안쓴다..) 차집합은 A - B !!
마치 비트연산처럼 활용 가능하다. 얼마나 놀라운가?
자 그럼 대망의 시간복잡도를 다른 자료구조들과 비교해보자.
들어가기전 set은 순서가 없다고 도입부분 특징에서 말했었다.
그러므로 indexing이라는 개념이 없다.
내가 자주쓰는 Operation 순으로 분석하겠다.
Big-O : O(1)
- x in set(S) , x not in set(S)
- S.remove(x) : 데이터 x 삭제 (x가 존재하지 않으면 에러)
- S.distinct(x) : 데이터 x 삭제 (x가 존재하지 않아도 에러가 안남)
- S.add(x)
- S.pop()
- S.clear()
- len(s)
remove와 distinct는 둘다 데이터 x를 삭제하는데 차이점은 remove 는 데이터 x 가 존재함을 보장하고 (없을시 에러) distinct는 존재를 보장하지 않으므로 데이터가 없는데 지워도 정상적으로 동작한다.
또한 length 를 구하는 복잡도가 1이라는건 정말 의외였다.
Big-O : O(n)
set S에는 n개의 데이터가 들어가있다고 가정
- set([1, 2, 3, 4, 5]) : initialization
- ==, !=, <=, <, 이런 작업들은 잘 사용하지 않으므로 패스
Bit-O : O(n + m)
set S1 의 size는 n
set S2 dml size는 m
- S1 & S2
- S1 - S2
- S1 ^ S2
- S1 | S2
위에서 사용한 집합연산을 사용하는건 전부 O(n + m)이다.
왜 빠를까?
파이썬의 set은 사실 hashset이다.
set을 console에 찍어보면
>>> A = set([1, 2, 3])
{1, 2, 3}이렇게 뜬다.
뭐가 이상하지 않나? 왜 헷갈리게 dictionary처럼 {}로 표현해놨냐고!!
왜냐면 둘 다 hash 구조이기 때문이다.
차이점으로 dict는 key와 value 구조로 저장되어 있고 set은 key값만 저장한다.
그렇게 되면 set의 어떤 x라는 key를 접근할때 항상 시간복잡도는 O(1) 이다!!
뭐 중복제거는 없으면 flag를 켜주고 있다면 그냥 냅두면 되니까 중복제거가 간단하다.
python dict와 set이 어떻게 만들어졌나 궁금하면 아래 링크를 참조하자 (들어가보면 궁금증이 싹 사라질것이다. 그게 해결이라서 라고는 장담 못하지만...)
https://hg.python.org/cpython/file/ec91ee7d9d8d/Objects/dictobject.c
https://hg.python.org/cpython/file/ec91ee7d9d8d/Objects/setobject.c
내가 가장 궁금했던건 x in S 가 어떻게 O(1)이 걸릴까? 였다.
set의 pop를 어떻게 구현했나를 보자.
static PyObject *
set_pop(PySetObject *so)
{
register Py_ssize_t i = 0;
register setentry *entry;
PyObject *key;
assert (PyAnySet_Check(so));
if (so->used == 0) {
PyErr_SetString(PyExc_KeyError, "pop from an empty set");
return NULL;
}
/* Set entry to "the first" unused or dummy set entry. We abuse
* the hash field of slot 0 to hold a search finger:
* If slot 0 has a value, use slot 0.
* Else slot 0 is being used to hold a search finger,
* and we use its hash value as the first index to look.
*/
entry = &so->table[0];
if (entry->key == NULL || entry->key == dummy) {
i = entry->hash;
/* The hash field may be a real hash value, or it may be a
* legit search finger, or it may be a once-legit search
* finger that's out of bounds now because it wrapped around
* or the table shrunk -- simply make sure it's in bounds now.
*/
if (i > so->mask || i < 1)
i = 1; /* skip slot 0 */
while ((entry = &so->table[i])->key == NULL || entry->key==dummy) {
i++;
if (i > so->mask)
i = 1;
}
}
key = entry->key;
Py_INCREF(dummy);
entry->key = dummy;
so->used--;
so->table[0].hash = i + 1; /* next place to start */
return key;
}전부 다 볼필요는 없다. 저 안의 while문을 보면 key값이 NULL이거나 key값에 dummy data가 들어있으면 계속 key를 늘린다. 즉 값이 있는 key가 나올때까지 순회한다는 것 이다.
그렇다면 최악의상황일때를 따지는 Big-O 표기법에서는 O(n)이 걸리는거 아닌가?
사실 논리적으로는 맞다. 그러나 파이썬은 이미 우리가 걱정하는걸 전부 해결해 놓았다. 훨씬 빠른 탐색 알고리즘을 적용하여 그런 말도 안되는 최악의 상황은 발생할일이 거의 전무후무하다.
그러므로 x in S는 '평균'적으로 O(1)이 걸린다는 것 이다.
또 위에서 놀라웠던 len(S)가 O(1)이라는것 !!
set_len(PyObject *so)
{
return ((PySetObject *)so)->used;
}위 set의 len 메서드를 보면 so 라는 PySetObject의 used를 그냥 가져온다.
너무 깊게 들어가면 머리가 빠질게 분명하므로 직독직해를 해보자면 Pyobject 포인터로 가져온 so를 PySetObject 포인터로 변환을 시켜주고 저장되어있던 used를 그냥 호출해서 return하는거로 해석이 된다.
그렇다면 so->used에 key가 insert 될때마다 증가된다는 증거를 가져오면 되겠지?
set_insert_key(register PySetObject *so, PyObject *key, long hash)
{
register setentry *entry;
assert(so->lookup != NULL);
entry = so->lookup(so, key, hash);
if (entry == NULL)
return -1;
if (entry->key == NULL) {
/* UNUSED */
so->fill++;
entry->key = key;
entry->hash = hash;
so->used++;
} else if (entry->key == dummy) {
/* DUMMY */
entry->key = key;
entry->hash = hash;
so->used++;
Py_DECREF(dummy);
} else {
/* ACTIVE */
Py_DECREF(key);
}
return 0;
}찾는데 한참 걸렸다.
보면 key가 NULL이거나 dummy일때만 insert를 해주면서 used를 증가시켜주고 존재한다면 증가시켜주지 않는다.
이제 set을 조금 더 유연하게 사용할 수 있을 것 같다.^~^

