세그먼트 트리

여러 개의 데이터가 연속적으로 존재할 때 특정한 범위의 데이터의 합을 구하는 방법

• 일반적인 구간합 → O(N)

• 세그먼트 트리 → O(logN)

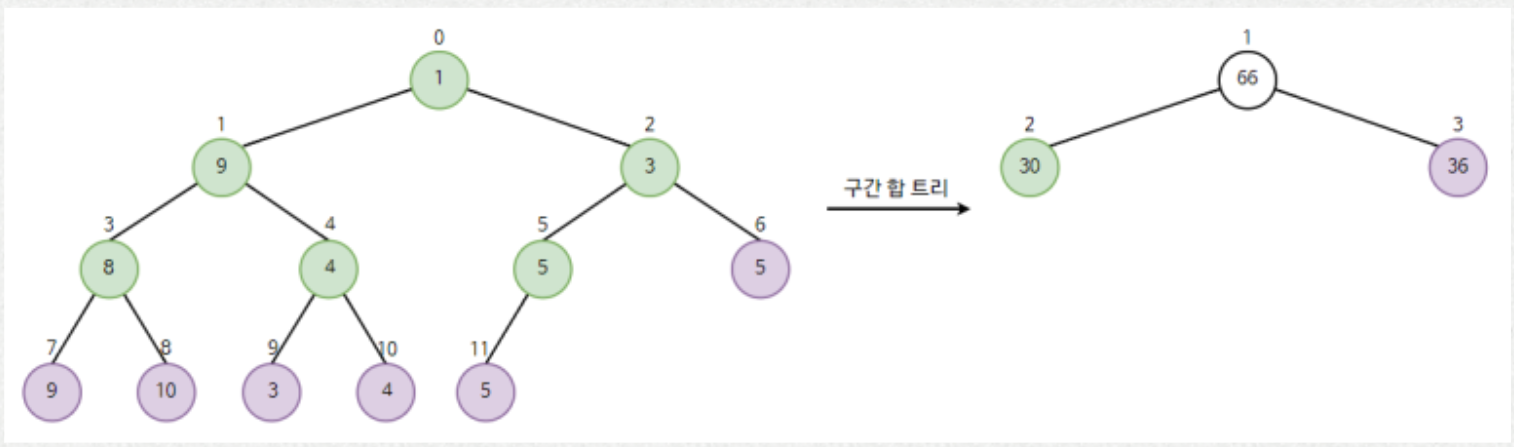
이런 식으로 구간 합 트리를 구한다.

특이점으로는 인덱스가 1부터 시작한다.

이유는 1 * 2 를 하면 왼쪽 자식의 노드가 나오도록 구현하기 위해서 이다.

필요한 변수

tree []
→ 크기는 리프노드의 갯수가 n개라고 치면 n개의 리프노드를 갖기 위해 필요한 높이의 2의 제곱만큼

ex) h == 3 → 2 ^ 3
h는 노드 개수에서 가장 가까운 2의 제곱수로 하면 된다.

ex ) n = 5 → h → log(8) : 3
그렇다면 크기 식은 $h = \log_2N + 1$ $size = 2^h$

필요한 메서드

l = [1, 9, 3, 8, 4, 5, 5, 9, 10, 3, 4, 5]

init ()

세그먼트 트리를 만들어줌

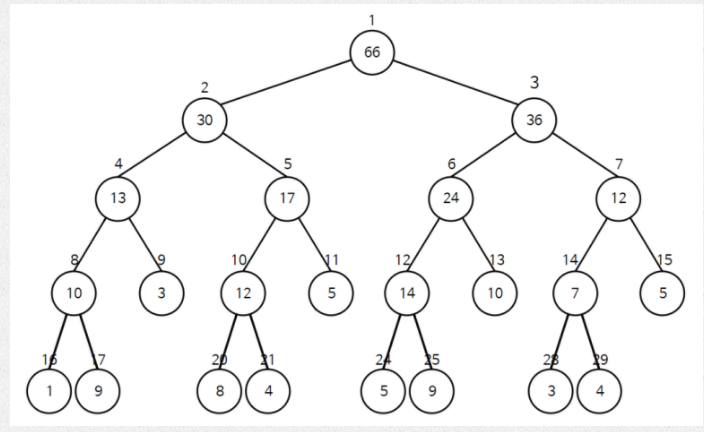
sum ()

파라미터를 받아 부분 합을 계산

단순히 범위 안에 있는 경우에 한해서 더해주면 된다.

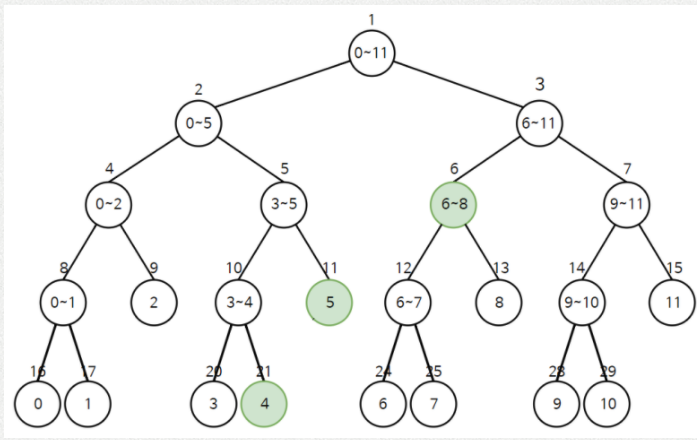
구현하기

import math

def init_segment_tree(start, end, node):
    """
    :param start: 시작 인덱스
    :param end: 끝 인덱스
    :param node: 구간합 트리의 노드 번호
    :return: 노드 번호를 인덱스로 갖는 구간합
    """
    if start == end:
        tree[node] = l[start]
    else:
        mid = (start + end) // 2
        tree[node] = init_segment_tree(start, mid, node * 2) + init_segment_tree(mid + 1, end, node * 2 + 1)
    return tree[node]


def sum_segment_tree(start, end, node, left, right):
    """
    :param start: 시작 인덱스
    :param end: 끝 인덱스
    :param node: 구간합 트리의 노드 번호
    :param left: 구간합을 찾고자 하는 범위의 왼쪽
    :param right: 구간합을 찾고자 하는 범위의 오른쪽
    :return: out of range -> return 0, 범위 안에 있는경우 -> return tree[node], 섞여있는 경우 -> 나눠서 sum
    """
    if left > end or right < start:
        return 0
    if left <= start and end <= right:
        print(f"sum to {tree[node]}")
        return tree[node]
    mid = (start + end) // 2
    return sum_segment_tree(start, mid, node * 2, left, right) + sum_segment_tree(mid + 1, end, node * 2 + 1, left, right)


def update_segment_tree(start, end, node, index, dif):
    """
    :param start: 시작 인덱스
    :param end: 끝 인덱스
    :param node: 구간합 트리의 노드 번호
    :param index: 바꾸려는 index
    :param dif: 이전 값과의 차이값
    """
    if index < start or index > end:
        return
    tree[node] += dif
    if start == end:
        return
    mid = (start + end) // 2
    update_segment_tree(start, mid, node * 2, index, dif)
    update_segment_tree(mid + 1, end, node * 2 + 1, index, dif)


if __name__ == "__main__":

    l = [1, 9, 3, 8, 4, 5, 5, 9, 10, 3, 4, 5]
    N = len(l)
    h = math.ceil(math.log2(N))
    size = 2 ** (h + 1)
    tree = [-1] * size
    init_segment_tree(0, N-1, 1)
    print(sum_segment_tree(0, N - 1, 1, 4, 8))
    print()