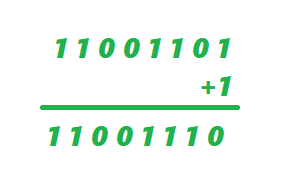CS | 1의 보수(1's Complement), 2의 보수(2's Complement)

🥔 1's Complement vs 2's Complement

| 컴퓨터는 어떻게 음수를 표현할까?

🥔 음수를 저장하는 방법

컴퓨터는 2진수만을 이해한다. 그렇다면 -5, -1, -32 같은 음수는 어떻게 저장할까?

이걸 해결하기 위한 대표적인 방법이 바로 1의 보수와 2의 보수다.

🥔 1의 보수(1’s Complement)

정의:

• 양수의 이진수를 반전(0 ↔ 1)시킨 값

• ex) 8비트로 5를 표현하고, 그 1의 보수를 구해보면

5 → 0000 0101
1's complement → 1111 1010

| 즉, -5를 1의 보수로 표현하면 11111010이다.

✅ 단점:

• 0을 +0 (00000000), -0 (11111111)으로 2가지 방식으로 표현

• 덧셈할 때 캐리 보정이 필요함

🥔 2의 보수(2’s Complement)

정의:

• 양수의 이진수를 1의 보수로 만들고, 거기에 +1을 더한 값

• 가장 널리 사용되는 음수 표현 방식

• 예시) 5의 2의 보수 표현

1단계: 5 → 0000 0101
2단계: 1's complement → 1111 1010
3단계: +1 → 1111 1011

=> -5의 2의 보수 표현 = 1111 1011

🥔 왜 2의 보수를 사용하는가?

특징	1의 보수	2의 보수
0의 표현 방식	+0, -0 두 가지	0은 오직 한 가지
연산의 단순함	캐리 보정 필요	덧셈/뺄셈 연산이 동일하게 작동
사용 여부	과거 일부 시스템	✅ 거의 모든 시스템 사용 중

| 2의 보수를 사용하면, 덧셈기 하나로 뺄셈도 처리 가능해 하드웨어가 단순해진다.

🥔 예제 비교

값	2진수 (8bit)	1's 보수	2's 보수
+5	00000101	00000101	00000101
-5	-	11111010	11111011

🥔 C++에서 확인

#include <iostream>
#include <bitset>
using namespace std;

int main() {
    int num = -5;
    cout << "Decimal: " << num << endl;
    cout << "Binary (2's complement): " << bitset<8>(num) << endl;
}

| 결과: 11111011 → 바로 2의 보수 표현임을 알 수 있다.