[프로그래머스 JavaScript] 피보나치 수

---

문제 링크

---

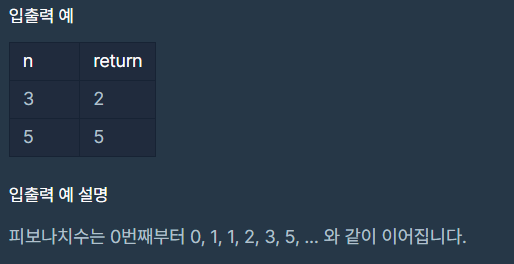
문제 설명
피보나치 수는 F(0) = 0, F(1) = 1일 때, 1 이상의 n에 대하여 F(n) = F(n-1) + F(n-2) 가 적용되는 수 입니다.

예를들어

F(2) = F(0) + F(1) = 0 + 1 = 1
F(3) = F(1) + F(2) = 1 + 1 = 2
F(4) = F(2) + F(3) = 1 + 2 = 3
F(5) = F(3) + F(4) = 2 + 3 = 5
와 같이 이어집니다.

2 이상의 n이 입력되었을 때, n번째 피보나치 수를 1234567으로 나눈 나머지를 리턴하는 함수, solution을 완성해 주세요.

제한 사항
n은 2 이상 100,000 이하인 자연수입니다.

---

나의 풀이

function solution(n) {
    var answer = 0;
    if (n < 2) {
        return n
    }
    return solution(n-2) + solution(n-1)
}

사용했던 함수를 재사용해서 풀었다. 하지만 시간 초과가 발생한다. 숫자가 커질수록 처리 능력이 배가 되어 느려지기 때문이다. 나눈 나머지를 리턴하는 함수라는 조건이 추가된 조건 같은데 이와 같은 경우를 대비하여 추가된 조건인 듯 하다.

---

이로 인한 새로운 풀이

function solution(n){
	var answer = []
    for(var i=0; i<=n; i++){
      if(i==0) answer.push(0)
      if(i==1) answer.push(1)
      if(i>=2){
        var sum = answer[i-1] + answer[i-2]
      	answer.push(sum % 1234567)
      }
    }
  var result = answer[n]
  return result 
}

//2023-08-02 리첵 완료