최대공약수와 최소공배수

최대공약수

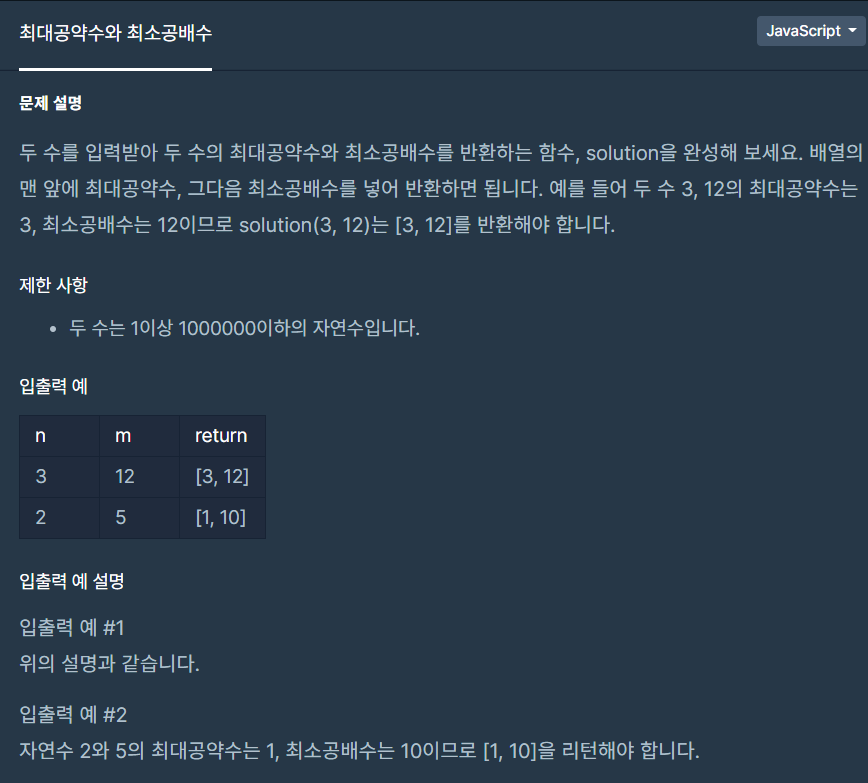
두 수, 혹은 그 이상의 여러 수의 공통인 약수 중 가장 큰 수
최대공약수는 아래 유클리드 호제법을 이용하여 풀 수 있다.

유클리드 호제법

호제법이란 말은 두 수가 서로(호:互) 상대방 수를 나누어(제:除)서 결국 원하는 수를 얻는 알고리즘을 나타낸다.

1)임의의 두 자연수 a,b가 주어졌을 때, 둘 중 큰 값이 a라고 가정하자.
2)a를 b로 나눈 나머지 값을 n이라고 설정한다.
3)이때 a와 b의 최대공약수는 b와 n의 최대공약수와 같다는 것을 활용할 수 있다.
4)이에 따라 b를 n으로 나눈 나머지 n'을 구하고, 다시 n을 n'으로 나눈 나머지를 구하는 과정을 반복하며 나머지가 0이 될 때 나누는 수가 a와 b의 최대공약수가 된다.

최소공배수

두 수, 혹은 그 이상의 여러 수의 공통인 배수 중 가장 작은 수
주어진 두 수 a, b를 곱한 후 두 수의 최대공약수로 나누는 방법으로 구할 수 있다.

풀이 1 (유클리드 호제법 이용)

function gcd(a, b) {
  // a가 b보다 클때만 아래 공식이 적용되므로 a가 b보다 큰 경우 아래와 같이 로직 처리
  if (a < b) {
    let temp = a;
    a = b;
    b = temp;
  }

  let n;
  while (b !== 0) {
    n = a % b; // 5 % 2 = 1
    a = b; // a = 2 할당
    b = n; // b = 1 할당 후 다시 n = a % b 실행... b가 0이 되면 멈춤
  }
  return a;
}

function lcm(a, b) {
  return (a * b) / gcd(a, b);
}

function solution11(a, b) {
  return [gcd(a, b), lcm(a, b)];
}

console.log(solution11(3, 12)); // [3,12]
console.log(solution11(2, 5)); //  [1,10]
console.log(solution11(270, 192)); //  [6,8640]

풀이 2

function solution12(n, m) {
  let answer = [];
  let lcm = 1;
  let gcd = 1;
  
  // 최대공약수 구하기
  let range = Math.min(n, m);
  for (let i = 1; i <= range; i++) {
    if (n % i === 0 && m % i === 0) {
      gcd = i;
    }
  }

  // 최소공배수 구하기
  for (let i = 1; i <= n * m; i++) {
    if (i % n === 0 && i % m === 0) {
      lcm = i;
      // 최소로 공통되는 배수만 찾으면 되므로 한번 찾으면 break로 for문을 빠져나옴
      break;
    }
  }

  answer.push(gcd, lcm);
  return answer;
}

console.log(solution12(3, 12)); // [3,12]
console.log(solution12(2, 5)); //  [1,10]
console.log(solution12(270, 192)); //  [6,8640]

참고자료

최대공약수 유클리드호제법 이용