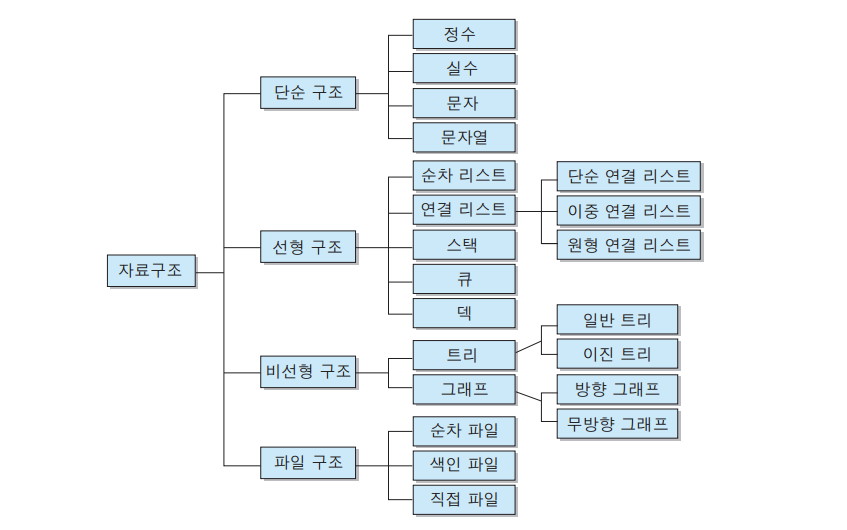
자료구조
자료의 집합으로, 각 원소들이 논리적으로 정의된 규칙에 의해 나열되며 자료에 대한 처리를 효율적으로 수행할 수 있도록 자료를 구분하여 표현한 것.
데이터를 정해진 규칙없이 저장하거나, 하나의 구조로만 정리하고 활용하는 것보다 데이터를 체계적으로 정리하여 저장해두는 게, 데이터를 활용하는 데 있어 훨씬 유리하다.
자료구조의 목적은 명확하다. 자료를 더 효율적으로 저장하고, 관리하기 위해 사용하며, 잘 선택된 자료구조는 실행시간을 단축시켜주거나 메모리 용량의 절약을 이끌어 낼 수 있다.
스택 & 큐
스택
- 자료를 보관할 수 있는 선형 구조
- 단, 넣을 때에는 한 쪽 끝에서 밀어 넣어야 하고(푸쉬)
- 꺼낼 때에는 같은 쪽에서 뽑아 꺼내야 한다.(팝)
- 후입선출(LIFO)
큐
- 자료를 보관할 수 있는 선형구조
- 단, 넣을 때에는 한 쪽 끈에서 밀어 넣아야 하고(인큐 연산)
- 꺼낼 때에는 반대 쪽에서 뽑아 꺼내야 하는 제약이 있음(디큐 연산)
- 선입선출(FIFO)
그래프
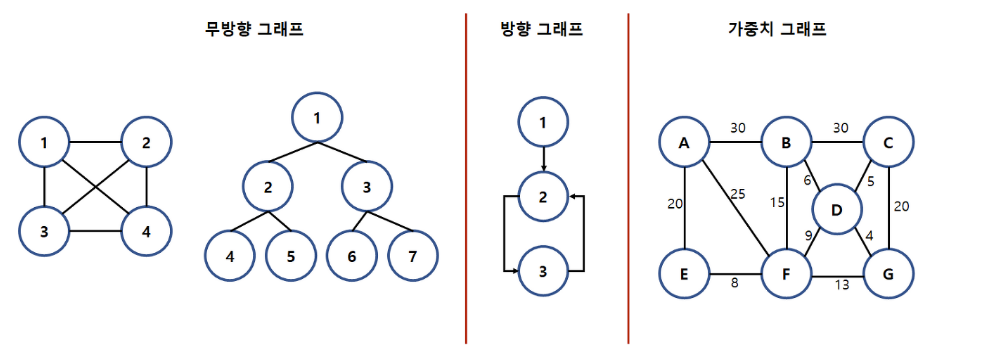
여러개의 점들이 서로 연결되어 있는 관계를 표현한 자료구조.
정점과 간선으로 이루어져 있다.
-
비가중치 그래프 : 추가적인 정보를 파악할 수 없는 그래프, 가중치가 적혀 있지 않은 그래프
-
가중치 그래프 : 간선에 연결정도를 표현한 그래프
-
무(방)향 그래프 : 두 정점을 연결하는 간선의 방향이 없는 그래프
-
방향 그래프 : 다이어그래프라고도 하며, 간선에 방향이 있는 그래프
-
진입차수(in-degree) / 진출차수(out-degree): 한 정점에 진입(들어오는 간선)하고 진출(나가는 간선)하는 간선이 몇 개인지를 나타낸다.
-
인접(adjacency): 두 정점 간에 간선이 직접 이어져 있다면 이 두 정점은 인접한 정점이다.
-
자기 루프(self loop): 정점에서 진출하는 간선이 곧바로 자기 자신에게 진입하는 경우 자기 루프를 가졌다 라고 표현한다. 다른 정점을 거치지 않는다는 것이 특징.
-
사이클(cycle): 한 정점에서 출발하여 다시 해당 정점으로 돌아갈 수 있다면 사이클이 있다고 표현한다. 내비게이션 그래프는 서울 —> 대전 —> 부산 —> 서울 로 이동이 가능하므로, 사이클이 존재하는 그래프이다.
그래프의 표현 방식 : 인접 행렬 & 인접 리스트
인접행렬
두 정점을 바로 이어주는 간선이 있다면 이 두 정점은 인접하다고 이야기한다.
인접 행렬은 서로 다른 정점들이 인접한 상태인지를 표시한 행렬로, 2차원 배열로 나타낸다.
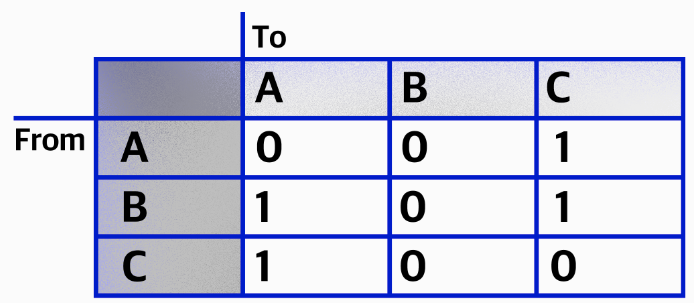
- A의 진출차수는 1개 입니다: A —> C
[0][2] === 1 - B의 진출차수는 2개 입니다: B —> A, B —> C
[1][0] === 1
[1][2] === 1 - C의 진출차수는 1개입니다: C —> A
[2][0] === 1
한 개의 큰 표와 같은 모습을 한 인접 행렬은 두 정점 사이에 관계가 있는지, 없는지 확인하기에 용이하다.
(예를 들어, A에서 B로 진출하는 간선이 있는지 파악하기 위해선 0 번째 줄의 1 번째 열에 어떤 값이 저장되어있는지 바로 확인할 수 있다.)
또한 가장 빠른 경로(shortest path)를 찾고자 할 때 주로 사용된다.
인접 리스트
각 정점이 어떤 정점과 인접한지를 리스트의 형태로 표현
각 정점마다 하나의 리스트를 가지고 있으며, 이 리스트는 자신과 인접한 다른 정점을 담고 있다.
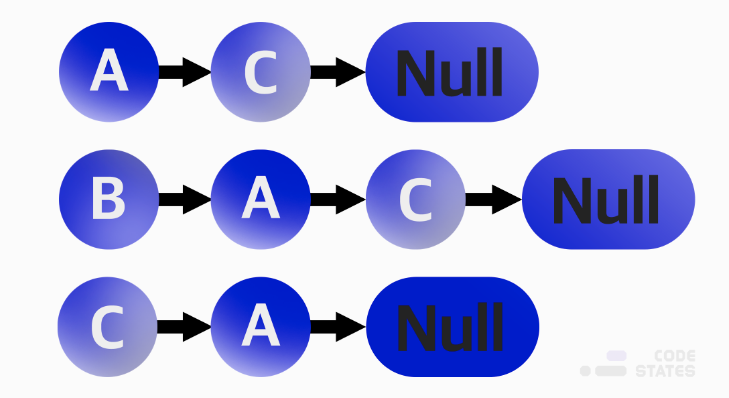
메모리를 효율적으로 사용하고 싶을 때 인접 리스트를 사용한다.
인접 행렬은 연결 가능한 모든 경우의 수를 저장하기 때문에 상대적으로 메모리를 많이 차지한다.
트리
그래프의 한 종류
단방향 그래프의 한 구조로, 데이터가 바로 아래에 있는 하나 이상의 데이터에 단방향으로 연결된 계층적 자료구조이다.
데이터를 순차적으로 나열시킨 선형 구조가 아니라, 하나의 데이터 뒤에 여러 개의 데이터가 존재할 수 있는 비선형 구조이다.
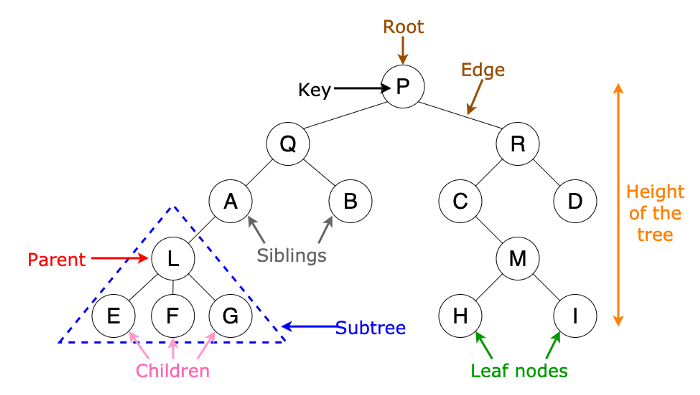
- 노드(Node) : 트리 구조를 이루는 모든 개별 데이터
- 루트(Root) : 트리 구조의 시작점이 되는 노드
- 부모 노드(Parent node) : 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 가까운 노드
- 자식 노드(Child node) : 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 먼 노드
- 리프(Leaf) : 트리 구조의 끝지점이고, 자식 노드가 없는 노드
BST 이진 탐색 트리


이진 탐색 트리(Binary Search Tree)는 모든 왼쪽 자식의 값이 루트나 부모보다 작고, 모든 오른쪽 자식의 값이 루트나 부모보다 큰 값을 가지는 특징
이진 트리, 이진 탐색트리 아래 정리
https://velog.io/@ellie12/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EA%B8%B0%EC%B4%88-1
이진트리 순회
.jpg)
전위순회
5 -> 2 -> 1 -> 4 -> 8 -> 6-> 9
루트 -> 왼쪽 -> 오른쪽
루트에서 시작해 왼쪽의 노드들을 순차적으로 둘러본 뒤, 왼쪽의 노드 탐색이 끝나면 오른쪽 노드를 탐색
중위순회
1-> 2 -> 4-> 5-> 6 -> 8-> 9
왼쪽 -> 루트 -> 오른쪽
제일 왼쪽 끝에 있는 노드부터 순회하기 시작하여, 루트를 기준으로 왼쪽에 있는 노드의 순회가 끝나면 루트를 거쳐 오른쪽에 있는 노드로 이동하여 마저 탐색
후위순회
1 -> 4 -> 2 -> 6 -> 9-> 8 -> 5
왼쪽 -> 오른쪽 -> 루트
제일 왼쪽 끝에 있는 노드부터 순회하기 시작하여, 루트를 거치지 않고 오른쪽으로 이동해 순회한 뒤, 제일 마지막에 루트를 방문
힙 heap
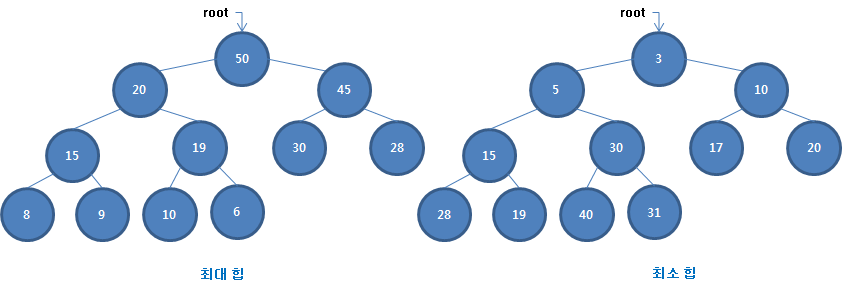
완전 이진 트리를 기본으로 한 자료구조
(시간복잡도 : O(log N))
heap의 종류
- 최대 힙 : 부모노드의 키값이 자식노드의 키값보다 항상 큰 힙
- 최소 힙 : 부모노드의 키값이 자식노드의 키값보다 항상 작은 힙
- 키값의 대소관계는 오로지 부모노드와 자식노드 간에만 성립하며, 특히 형제 사이에는 대소관계가 정해지지 않는다
