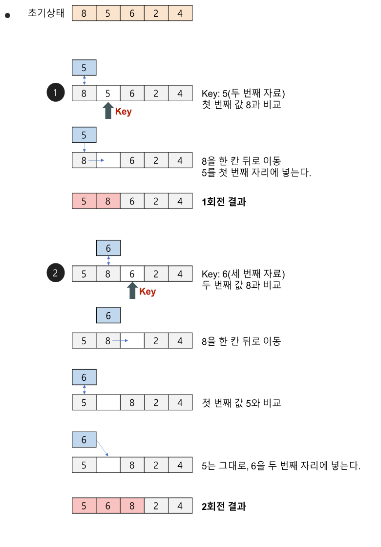
삽입 정렬
- 삽입 정렬은 두 번째 자료부터 시작하여 그 앞(왼쪽)의 자료들과 비교하여 삽입할 위치를 지정한 후 자료를 뒤로 옮기고 지정한 자리에 자료를 삽입하여 정렬하는 알고리즘이다.
- 즉, 두 번째 자료는 첫 번째 자료, 세 번째 자료는 두 번째와 첫 번째 자료, 네 번째 자료는 세 번째, 두 번째, 첫 번째 자료와 비교한 후 자료가 삽입될 위치를 찾는다. 자료가 삽입될 위치를 찾았다면 그 위치에 자료를 삽입하기 위해 자료를 한 칸씩 뒤로 이동시킨다.
- 처음 Key 값은 두 번째 자료부터 시작한다.
삽입 정렬(insertion sort) 알고리즘의 특징
장점
안정한 정렬 방법
레코드의 수가 적을 경우 알고리즘 자체가 매우 간단하므로 다른 복잡한 정렬 방법보다 유리할 수 있다.
대부분위 레코드가 이미 정렬되어 있는 경우에 매우 효율적일 수 있다.
단점
비교적 많은 레코드들의 이동을 포함한다.
레코드 수가 많고 레코드 크기가 클 경우에 적합하지 않다.
https://gmlwjd9405.github.io/2018/05/06/algorithm-insertion-sort.html
const insertionSort = function (arr) {
function repeat(idx) {
if (idx > arr.length - 1) {
return;
}
for (let i = 0; i < idx; i++) {
if (arr[i] > arr[idx]) {
let [frt, cur] = [arr[i], arr[idx]];
arr[i] = cur;
arr[idx] = frt;
}
}
repeat(idx + 1);
}
repeat(1);
return arr;
};
let output = insertionSort([5, 4, 3, 2, 1]);
console.log(output); // --> [1,2,3,4,5]퀵 정렬
큰 숫자를 왼쪽부터 차고, 작은 숫자를 오른쪽부터 찾는다.
과정 설명
- 리스트 안에 있는 한 요소를 선택한다. 이렇게 고른 원소를 피벗(pivot) 이라고 한다.
- 피벗을 기준으로 피벗보다 작은 요소들은 모두 피벗의 왼쪽으로 옮겨지고 피벗보다 큰 요소들은 모두 피벗의 오른쪽으로 옮겨진다. (피벗을 중심으로 왼쪽: 피벗보다 작은 요소들, 오른쪽: 피벗보다 큰 요소들)
- 피벗을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬한다.
- 분할된 부분 리스트에 대하여 순환 호출 을 이용하여 정렬을 반복한다.
- 부분 리스트에서도 다시 피벗을 정하고 피벗을 기준으로 2개의 부분 리스트로 나누는 과정을 반복한다. - 부분 리스트들이 더 이상 분할이 불가능할 때까지 반복한다.
- 리스트의 크기가 0이나 1이 될 때까지 반복한다.
const quickSort = function (arr) { function quick(arr, start, end) { if (start >= end) { return; } let key = start; let i = start + 1; let j = end; while (i <= j) { while (arr[i] <= arr[key]) { i++; } while (arr[j] >= arr[key] && j > start) { j--; } if (i > j) { let [frt, back] = [arr[key], arr[j]]; arr[key] = back; arr[j] = frt; } else { let [frt, back] = [arr[i], arr[j]]; arr[i] = back; arr[j] = frt; } } quick(arr, start, j - 1); quick(arr, j + 1, end); } quick(arr, 0, arr.length - 1); return arr; };
재귀함수 사용
const quickSort = function (arr) { if (arr.length <= 1) return arr; const pivot = arr[0]; const left = []; const right = []; for (let i = 1; i < arr.length; i++) { if (arr[i] <= pivot) left.push(arr[i]); else right.push(arr[i]); } const lSorted = quickSort(left); const rSorted = quickSort(right); return [...lSorted, pivot, ...rSorted]; };
장점
- 속도가 빠르다.
- 시간 복잡도가 O(nlog₂n)를 가지는 다른 정렬 알고리즘과 비교했을 때도 가장 빠르다.
- 추가 메모리 공간을 필요로 하지 않는다.
- 퀵 정렬은 O(log n)만큼의 메모리를 필요로 한다.
단점
- 정렬된 리스트에 대해서는 퀵 정렬의 불균형 분할에 의해 오히려 수행시간이 더 많이 걸린다.
- 퀵 정렬의 불균형 분할을 방지하기 위하여 피벗을 선택할 때 더욱 리스트를 균등하게 분할할 수 있는 데이터를 선택한다.
- EX) 리스트 내의 몇 개의 데이터 중에서 크기순으로 중간 값(medium)을 피벗으로 선택한다.
버블 정렬
선택 정렬
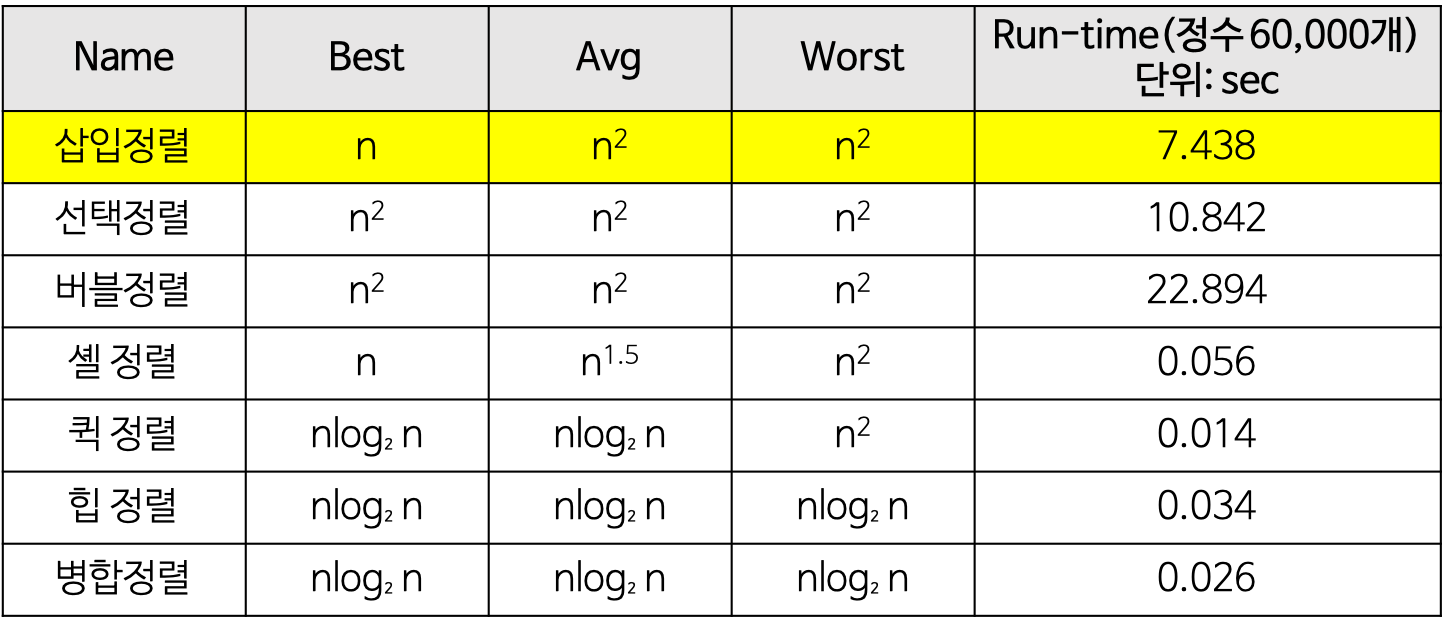
참고
알고리즘 정리 블로그
