| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞힌 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 2 초 | 512 MB | 51039 | 14330 | 9949 | 25.664% |
문제
수빈이는 동생과 숨바꼭질을 하고 있다. 수빈이는 현재 점 N(0 ≤ N ≤ 100,000)에 있고, 동생은 점 K(0 ≤ K ≤ 100,000)에 있다. 수빈이는 걷거나 순간이동을 할 수 있다. 만약, 수빈이의 위치가 X일 때 걷는다면 1초 후에 X-1 또는 X+1로 이동하게 된다. 순간이동을 하는 경우에는 1초 후에 2*X의 위치로 이동하게 된다.
수빈이와 동생의 위치가 주어졌을 때, 수빈이가 동생을 찾을 수 있는 가장 빠른 시간이 몇 초 후인지 그리고, 가장 빠른 시간으로 찾는 방법이 몇 가지 인지 구하는 프로그램을 작성하시오.
입력
첫 번째 줄에 수빈이가 있는 위치 N과 동생이 있는 위치 K가 주어진다. N과 K는 정수이다.
출력
첫째 줄에 수빈이가 동생을 찾는 가장 빠른 시간을 출력한다.
둘째 줄에는 가장 빠른 시간으로 수빈이가 동생을 찾는 방법의 수를 출력한다.
답안
import heapq
import sys
RANGE_END = 200_000
source, destination = map(int, sys.stdin.readline().split())
memo = [[0, 0] for _ in range(RANGE_END)]
memo[source] = [0, 1]
def update_memoization(steps, position):
if memo[position] == [0, 0]:
memo[position] = [steps, 1]
elif memo[position][0] == steps:
memo[position][1] += 1
else:
return False
return True
pq = [(0, source)]
while pq:
steps, position = heapq.heappop(pq)
answer_step = memo[destination][0]
if answer_step != 0 and steps > answer_step:
continue
for adjacent in [2*position, position-1, position+1]:
if not (0 <= adjacent < RANGE_END):
continue
if update_memoization(steps+1, adjacent):
heapq.heappush(pq, (steps+1, adjacent))
answer_step, answer_count = memo[destination]
print(answer_step, answer_count, sep='\n')풀이
수빈이의 위치로부터 동생의 위치로 가는 최단 경로를 구하는 문제이지만, 그 최단 경로의 방법의 수도 구해야 한다.
최단 경로의 거리만을 구한다면 일반적인 BFS로 쉽게 풀릴 수 있으나, 방법의 수를 구하기 위해서는 추가적인 구현이 필요하다.
예를 들어, 아래와 같은 그림에서 1에서 9까지 가는 최단 경로들을 생각해보자.
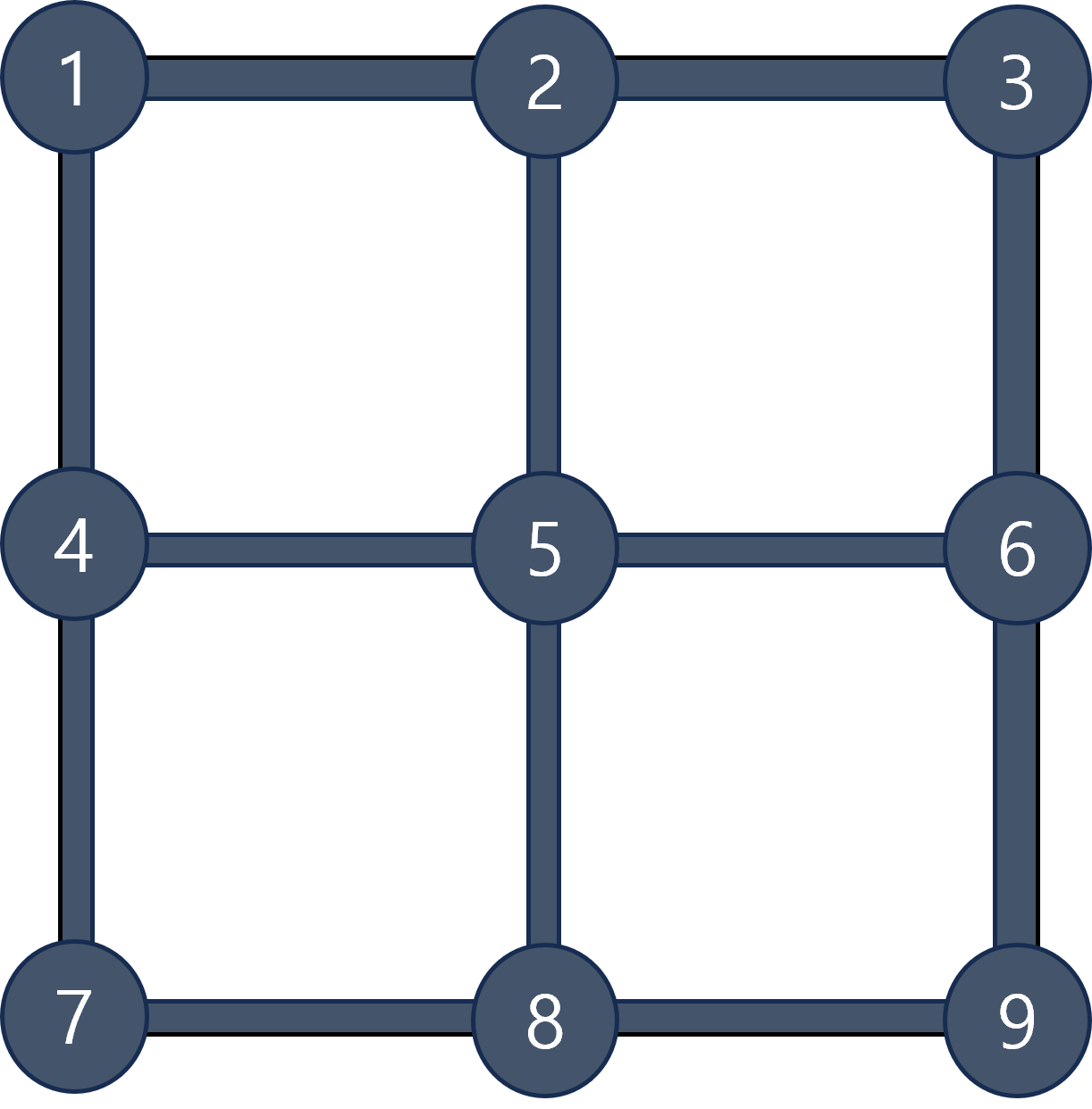
최단 경로는 4이지만, 아래와 같이 여러 가지 최단 경로가 존재한다.

- 1→4→7→8→9
- 1→4→5→8→9
- 1→4→5→6→9
- 1→2→5→8→9
- 1→2→5→6→9
- 1→2→3→6→9
그런데 일반적인 BFS를 사용하면 이 중 하나의 최단 경로와 최단 거리를 구할 수는 있겠으나, 모든 최단 경로의 경우의 수를 탐색하지는 못하게 될 것이다.
왜냐하면 일반적인 BFS에서는 어떤 칸에 접근한 적이 있는지 기록하고, 만약 이전에 접근했던 적이 있었다면 그 칸의 접근을 아예 막기 때문이다.
따라서 visited가 아닌 다른 방법을 고안해내야 한다.
그래서 내가 생각했던 방법은 아래와 같이 각 좌표마다 메모이제이션을 하는 것이었다.
memo = [[0, 0] for _ in range(RANGE_END)]
memo[source] = [0, 1]memo 배열에는 (이 점까지 최단경로로 도달할 때 지금까지 지난 시간(시작점으로부터의 거리), 이 점까지 최단 경로로 도달하는 경우의 수)가 저장되게 된다.
def update_memoization(steps, position):
if memo[position] == [0, 0]:
memo[position] = [steps, 1]
elif memo[position][0] == steps:
memo[position][1] += 1
else:
return False
return True그리고 이 memo 배열은 위와 같이 update_memoization() 함수로 값이 변경되는데,
만약 위치가 position인 칸에 도달한 적이 없어 초기화된 상태 그대로([0, 0])이면, 이 점까지 최단 경로로 도달하는 경우 시작점으로부터의 거리를 저장한다.
그리고 만약 그와 동일한 칸에 다시 한번 도달하였고, 이 경우 또한 최단 경로로 도달한 경우 경우의 수를 1 더해준다.
그렇지 않은 경우는 아무 것도 하지 않고, 그 이상의 탐색을 멈춘다.
이해를 돕기 위해 예시를 들자면, 아래와 같이 memo 배열이 있다고 해보자.
시작점은 1이고, 도착점은 7이다.

맨 처음에는 모든 배열이 [0,0]으로 초기화되어 있다. 초기 상태에서는 그 칸까지의 최단거리가 밝혀지지 않았으며(0), 최단 거리로 도달하는 경우의 수도 없다(0).

시작지가 1이다. 위치 1은, 시작점으로부터 최단 거리는 0이고, 최단 경로의 경우의 수는 1이다.
시작점부터, 그 수에 -1, 그 수에 +1, 그 수에 *2를 연산한 수를 각각 살펴본다.

시작점 1에서 1을 뺀 수는 0이다. 위치 0은, 시작점으로부터 최단 거리가 1이고, 경우의 수는 하나 추가되어 1이 된다.

시작점 1에서 1을 더한 수는 2이다. 위치 2는, 시작점으로부터 최단 거리가 1이고, 경우의 수는 하나 추가되어 1이 된다.

시작점 1에서 2을 곱한 수는 2이다. 위치 2는, 시작점으로부터 최단 거리가 1이고, 경우의 수는 하나 추가되어 2가 된다.
최단 경로를 찾기 위해, 가장 짧은 거리를 가진 칸들로부터 다시 시작한다.
위치 0과 위치 2에 있는 칸이 거리 1로 가장 짧은 거리를 가졌으므로, 위치 0을 먼저 살펴본다.

기준점 0에서 1을 뺀 수는 -1이다. 위치 -1은 범위를 넘어서므로 더이상 고려하지 않는다.
기준점 0에서 1을 더한 수는 1이다. 가장 짧은 거리를 가진 칸들을 우선적으로 살펴왔으므로, 그 전에 기록된 거리보다 더 짧은 거리일 수는 없다. 이 경우 또한 무시된다.
기준점 0에서 2을 곱한 수는 0으로, 위와 같은 이유로 무시된다.
그 다음으로 살펴볼 것은 가장 짧은 거리 1을 가진 위치 2이다.

기준점 2에서 1을 뺀 수는 1이다. 0보다 거리가 짧지 않으므로 더이상 고려하지 않는다.
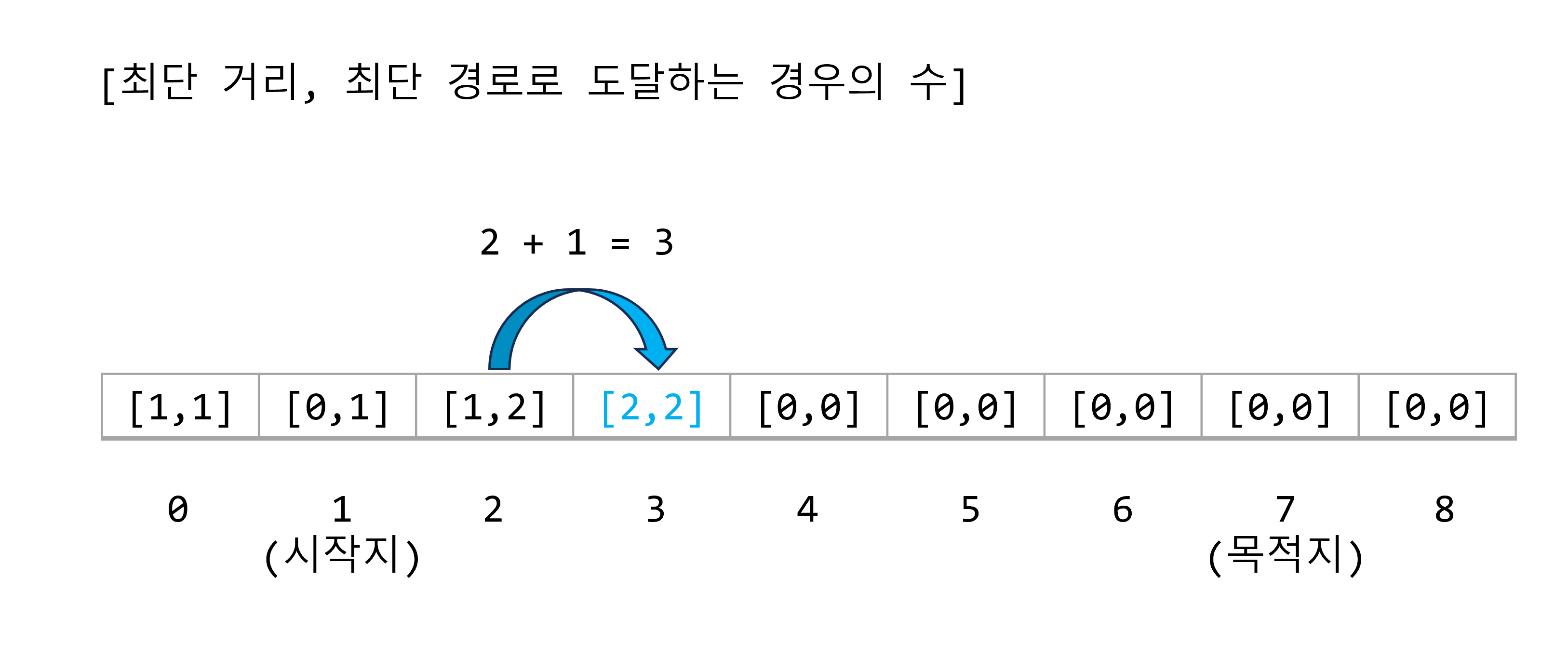
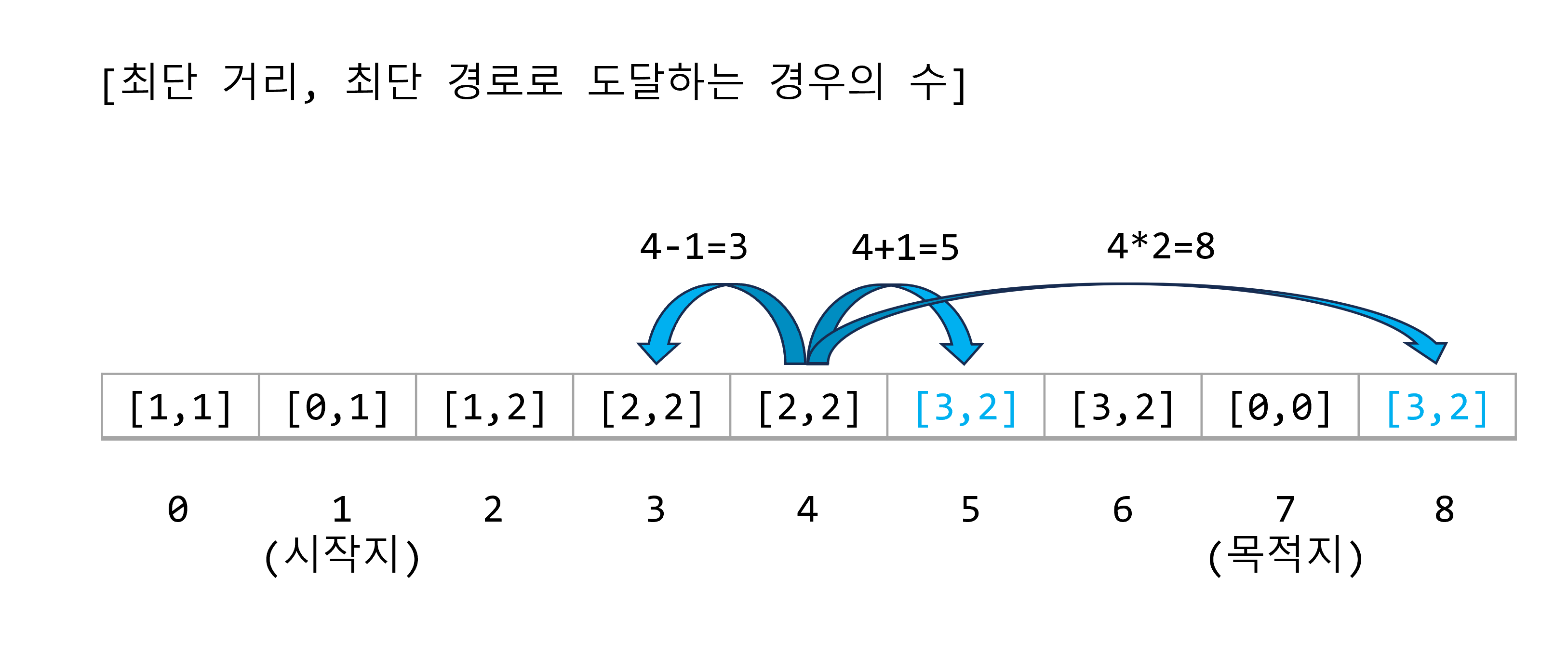
기준점 2에서 1을 더한 수는 2이다. 위치 3은, 시작점으로부터 최단 거리가 2이고, 경우의 수는 2가 된다.
이때, 위치 2에 최단 거리 1로 도달하는 경우의 수가 2개이므로(1+1=2, 12=2) 위치 2에서 1을 더함으로써 위치 3에 도달하는 경우의 수도 2개가 된다(1+1+1=3, 12+1=3).
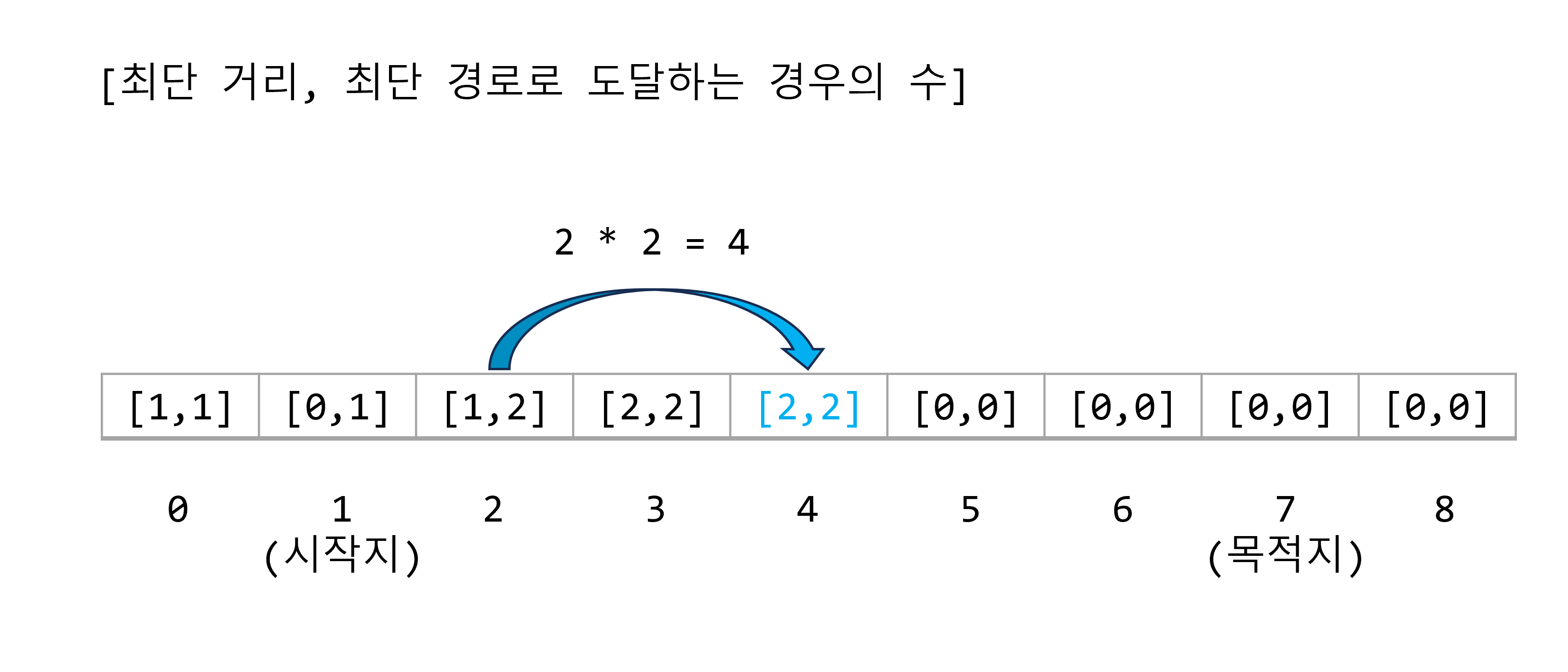
기준점 2에서 2을 곱한 수는 4이다. 위치 4는, 시작점으로부터 최단 거리는 2이고, 경우의 수는 2가 된다.
최단거리가 1인 모든 위치를 살펴보았으므로, 그 다음으로는 최단거리가 2인 위치들을 살펴볼 차례이다.
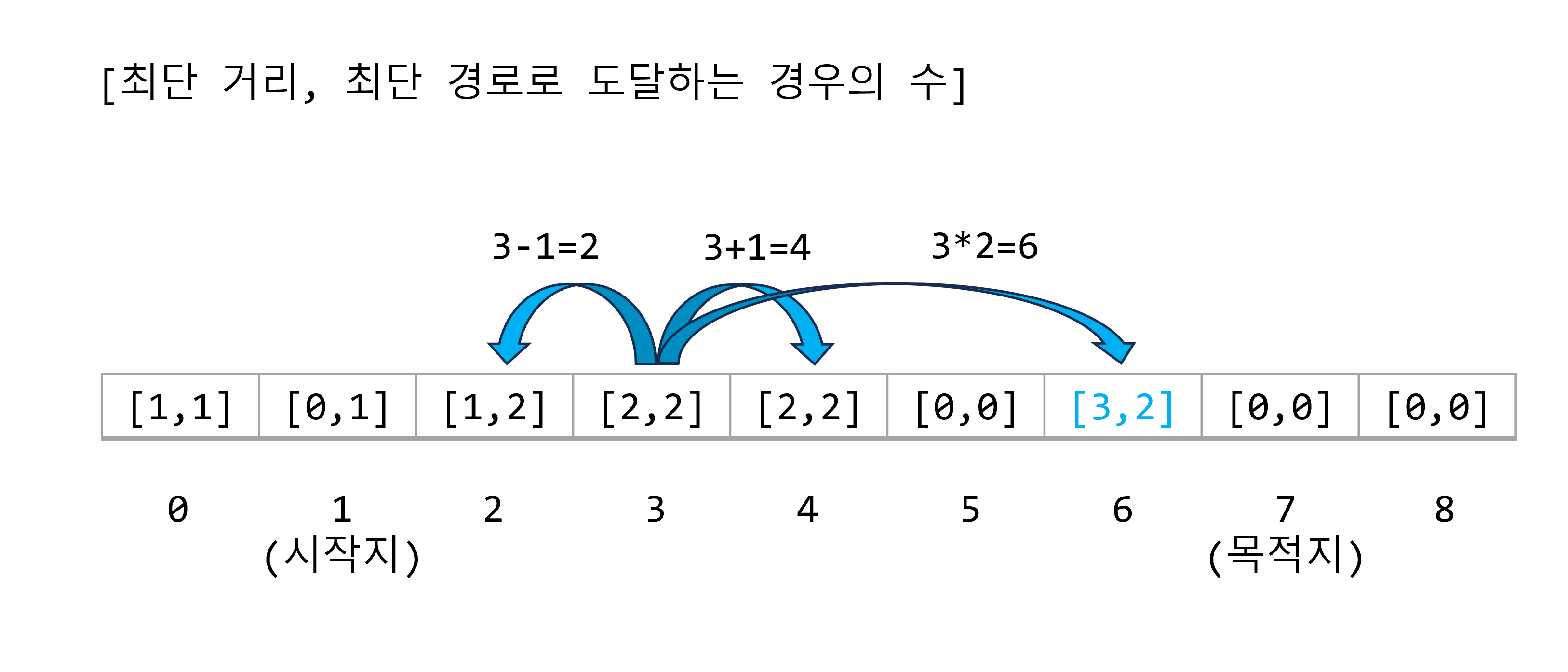
기준점 3에서 1을 뺀 수인 위치 2와, 1을 더한 수인 위치 4의 경우, 각각 기록된 최단거리 1, 2보다 더 거리가 짧지 않으므로 무시된다.
기준점 3에서 2을 곱한 수는 6이다. 위치 6은, 시작점으로부터 최단 거리가 3이고, 경우의 수는 2가 된다.
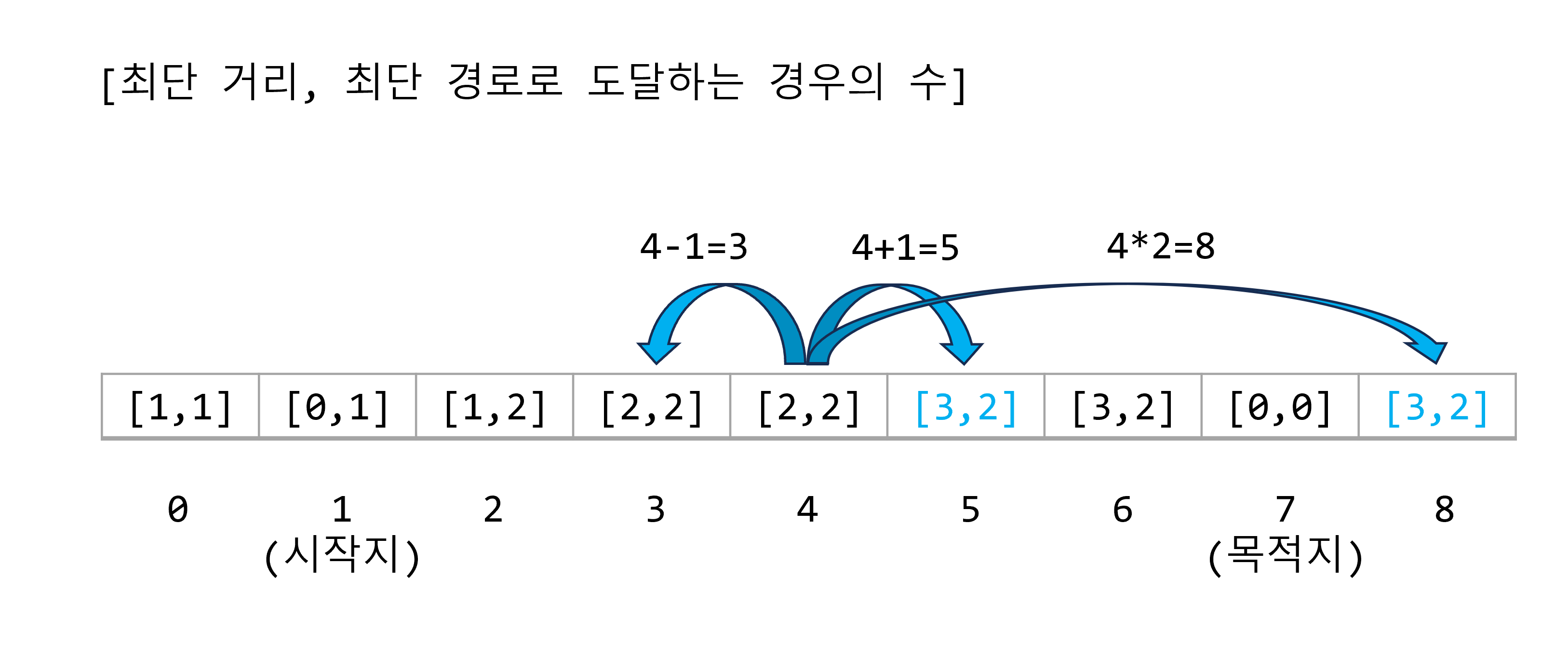
기준점 4에서 1을 뺀 수인 위치 3의 경우, 해당 위치에 기록된 최단거리 2보다 더 거리가 짧지 않으므로 무시된다.
기준점 4에서 1을 더한 수는 5이다. 위치 5는, 시작점으로부터 최단 거리가 3이고, 경우의 수는 2가 된다.
기준점 4에서 2을 곱한 수는 6이다. 위치 6은, 시작점으로부터 최단 거리가 3이고, 경우의 수는 2가 된다.
최단거리가 2인 모든 위치를 살펴보았으므로, 그 다음으로는 최단거리가 3인 위치들을 살펴볼 차례이다.
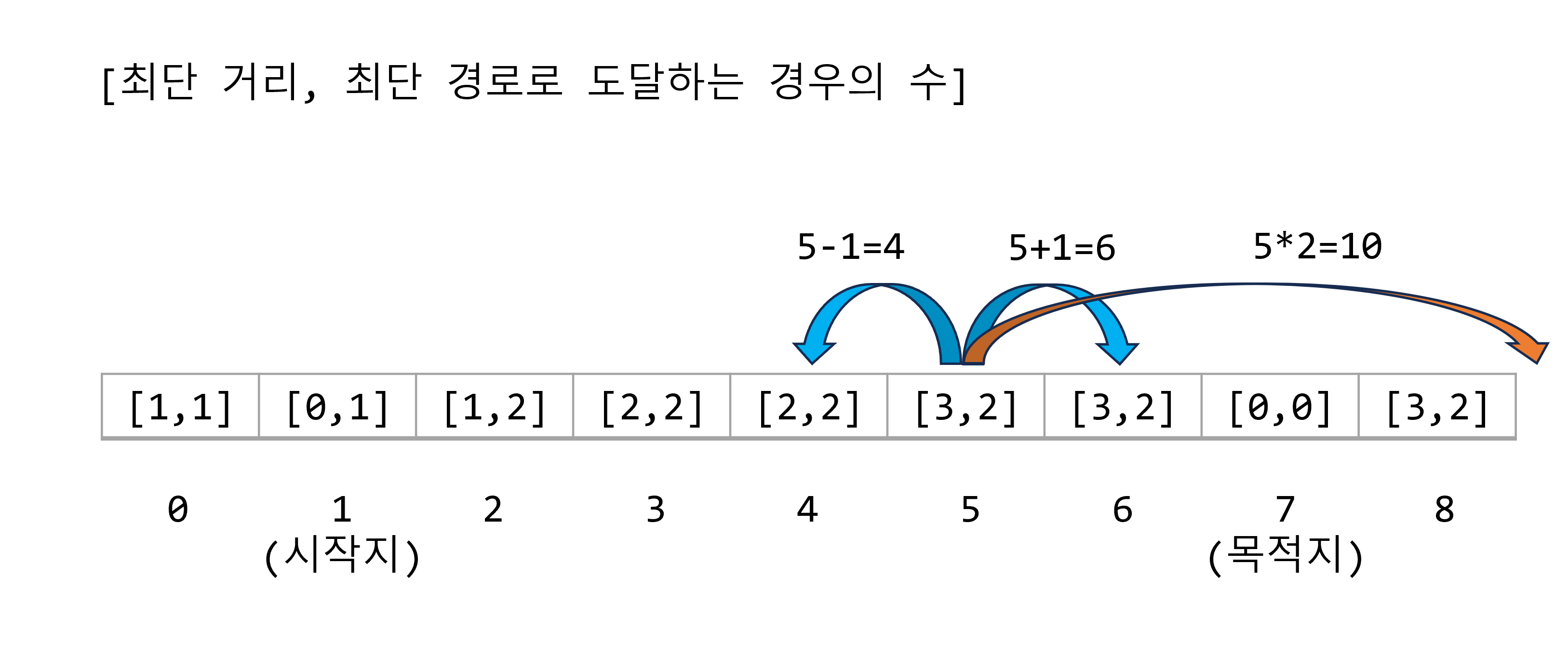
기준점 5에서 1을 뺀 수인 위치 4와, 1을 더한 수인 위치 6의 경우, 각각 기록된 최단거리 2, 3보다 더 거리가 짧지 않으므로 무시된다.
기준점 5에서 2를 곱한 수는 10이다. 위치 10은 범위를 넘어서므로 더이상 고려하지 않는다.
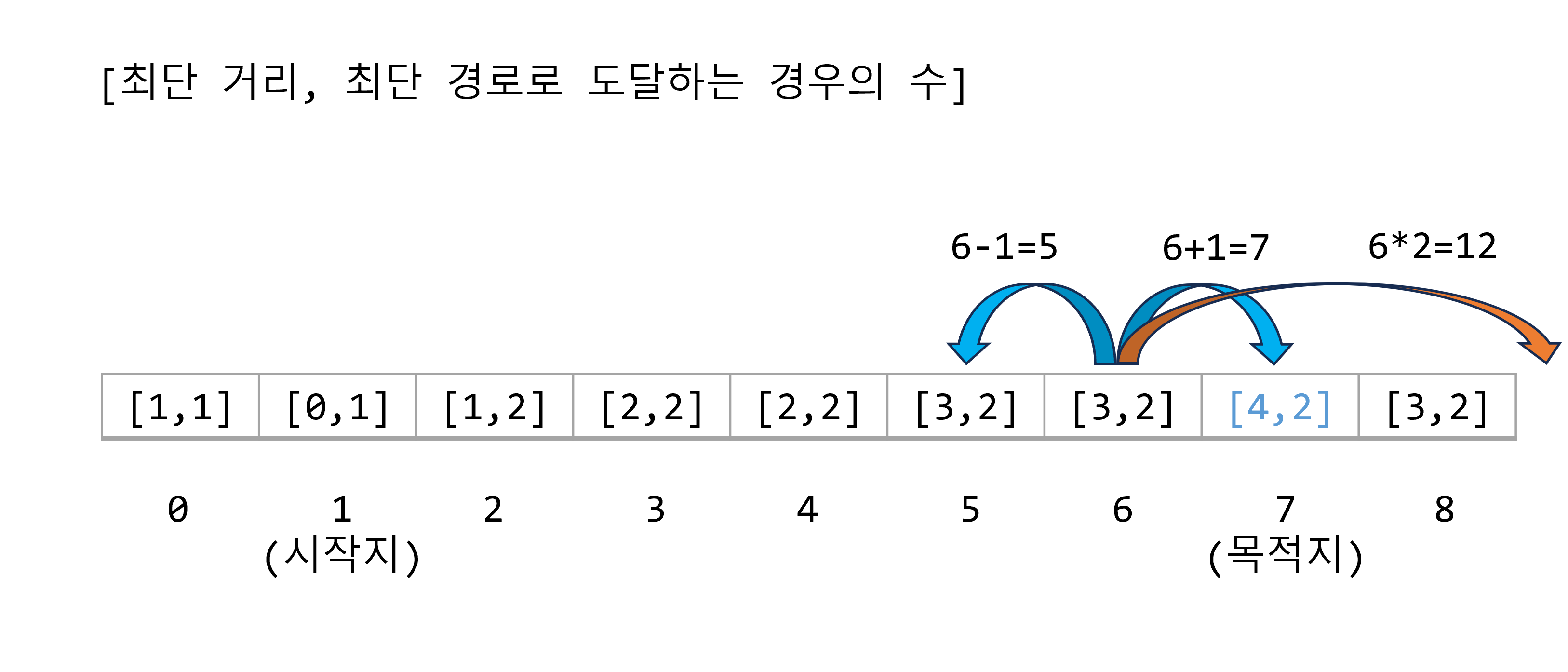
기준점 6에서 1을 뺀 수인 위치 5의 경우, 해당 위치에 기록된 최단거리 3보다 더 거리가 짧지 않으므로 무시된다.
기준점 6에서 1을 더한 수는 7이다. 위치 7은, 시작점으로부터 최단 거리가 4이고, 경우의 수는 2가 된다.
기준점 6에서 2를 곱한 수는 12이다. 위치 12는 범위를 넘어서므로 더이상 고려하지 않는다.

기준점 8에서 1을 뺀 수인 위치 7의 경우, 거리 4로 도달이 가능하며, 이는 위치 7에 기록된 최단거리와 같다. 그러므로, 최단거리로 도달하는 경우의 수를 기존 2에서 더해주어야 한다. 8에서 1을 뺌으로써 7에 도달하는 경우의 수 2를 더해준다.
기준점 8에서 1을 더한 수는 9이고, 2를 곱한 수는 16이다. 위치 9와 위치 16은 범위를 넘어서므로 더이상 고려하지 않는다.
목적지에 변경이 일어나지 않을 때까지 이러한 과정들을 거치면 문제에서 요구하는 답을 구할 수 있다.
1에서부터 7까지의 최단 거리는 4, 그리고 최단 경로로 도달하는 경우의 수가 4가 되는 것이다.
정리하면, 로직은 다음과 같다.
- 기록된 최단 거리가 짧은 위치들부터, 메모이제이션 배열의 값을 아래와 같이 변경한다.
- 만약 어떠한 위치에 맨 처음 방문하여 그 위치에 기록된 최단 거리가 0이면, (현재 위치에 기록된 최단 거리 + 1, 현재 위치에 기록된 경우의 수)를 그 위치에 기록한다.
- 만약 어떠한 위치에 이미 방문한 적이 있고, 그 위치에 기록된 최단 거리가 현재 위치의 최단 거리 + 1과 같은 경우, 그 위치에 경우의 수를 더해준다.
- 만약 어떠한 위치에 이미 방문한 적이 있지만, 그 위치에 기록된 최단 거리가 현재 위치의 최단 거리보다 더 작을 경우, 갱신하지 않고, 그 이후의 탐색을 종료한다.
def update_memoization(steps, position):
if memo[position] == [0, 0]:
memo[position] = [steps, 1]
elif memo[position][0] == steps:
memo[position][1] += 1
else:
return False
return True그것을 코드로 옮긴 것이 위 부분이고, 이러한 로직을 BFS와 함께 진행시키면 된다.
