| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞힌 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 0.1 초 (https://www.acmicpc.net/problem/9252#) | 256 MB | 39123 | 14323 | 11089 | 37.946% |
문제
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.
예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.
입력
첫째 줄과 둘째 줄에 두 문자열이 주어진다. 문자열은 알파벳 대문자로만 이루어져 있으며, 최대 1000글자로 이루어져 있다.
출력
첫째 줄에 입력으로 주어진 두 문자열의 LCS의 길이를, 둘째 줄에 LCS를 출력한다.
LCS가 여러 가지인 경우에는 아무거나 출력하고, LCS의 길이가 0인 경우에는 둘째 줄을 출력하지 않는다.
답안
import sys
sys.setrecursionlimit(1_000_100)
str1 = sys.stdin.readline().rstrip()
str2 = sys.stdin.readline().rstrip()
memo = [[0]*(len(str2)+1) for _ in range(len(str1)+1)]
def lcs():
memo_max_pos = [0, 0]
memo_max_value = 0
for i in range(1, len(str1)+1):
for j in range(1, len(str2)+1):
if str1[i-1] == str2[j-1]:
memo[i][j] = memo[i-1][j-1] + 1
if memo_max_value < memo[i][j]:
memo_max_value = memo[i][j]
memo_max_pos = [i, j]
continue
memo[i][j] = max(memo[i-1][j], memo[i][j-1])
return memo_max_pos, memo_max_value
def trace_back(start, value, reversed_result=[]):
row, col = start
up = memo[row-1][col]
left = memo[row][col-1]
if up == value:
return trace_back((row-1, col), value, reversed_result)
elif left == value:
return trace_back((row, col-1), value, reversed_result)
else:
reversed_result.append(str1[row-1])
if up == left == 0:
return ''.join(reversed(reversed_result))
return trace_back((row-1, col-1), value-1, reversed_result)
def solve():
start_pos, max_value = lcs()
print(max_value)
if max_value == 0:
return
result = trace_back(start_pos, max_value)
print(result)
solve()풀이
이 풀이는 LCS(최장 공통 부분 수열)의 길이를 묻는 다음 문제의 연장선상에 있으니, 최장 공통 부분 수열을 어떻게 DP를 이용해 구할 수 있는지 궁금하다면 다음 글을 참고하자.
위 글과 같은 과정을 거치면, memo에는 아래와 같이 0, 1, 2, …, n이 양파 껍질처럼 저장된다.
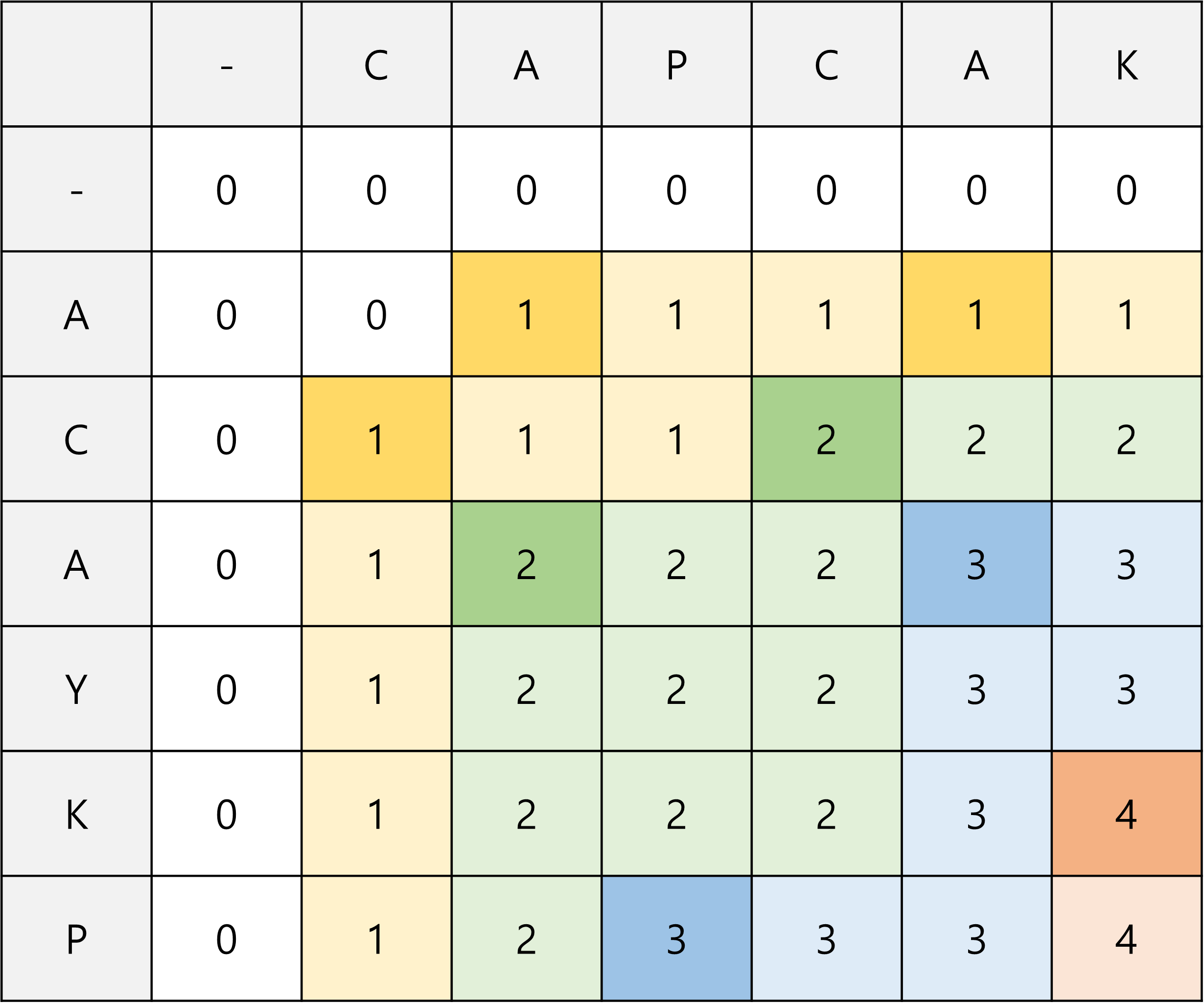
위 글의 문제에서는 LCS의 길이만을 물어보았기 때문에 memo의 최댓값을 출력하면 됐지만, 이 문제에서는 그 LCS의 실제 값을 물어보고 있다.
그런데 우리는 memo를 통해서 LCS의 실제 값을 구할 수 있다. memo의 맨 오른쪽 아래에서부터 왼쪽 위 방향으로 숫자가 작아지는 쪽으로 거슬러 올라가면서, 영역이 바뀌는 부분을 체크하면 되는 것이다.
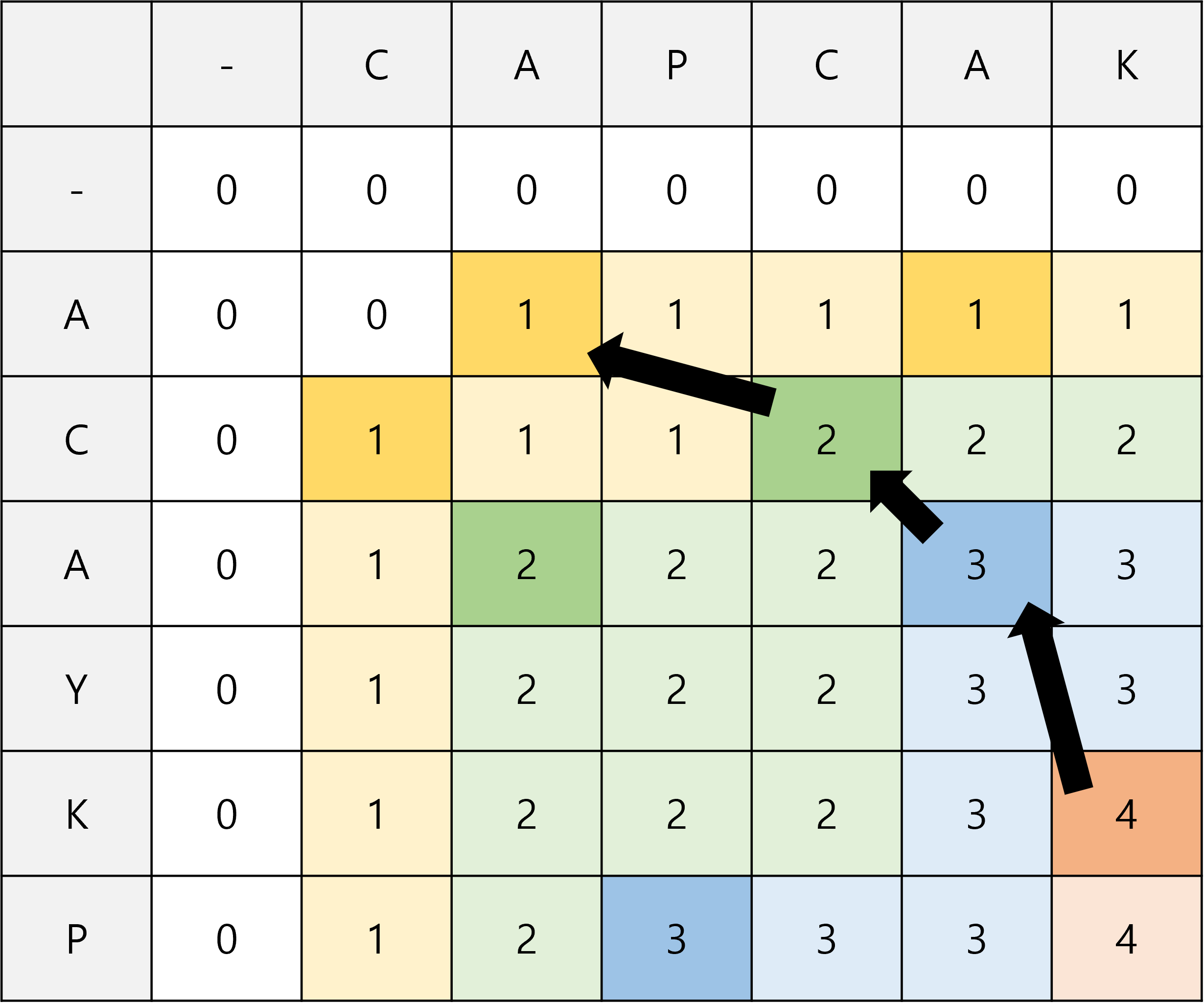
즉, 위와 같이 숫자가 작아지는 순서로 거슬러 올라가면 K, A, C, A 순서대로 체크를 하게 되고 이때 LCS의 값은 이 순서의 반대인 ACAK가 된다.
trace_back() 함수에서는 재귀를 활용해 거슬러 올라가는 로직을 짰다.
- 위쪽 칸이 현재 칸과 값이 같으면 위쪽으로 이동
- 왼쪽 칸이 현재 칸과 값이 같으면 왼쪽으로 이동
- 왼쪽 칸과 위쪽 칸이 모두 현재 칸보다 값이 작으면, 그 칸에 해당하는 문자를 저장한 뒤 왼쪽 위 대각선으로 이동
- 다만, 만약 해당 칸의 위쪽과 왼쪽 칸이 모두 0이면 재귀 종료
이때, 왼쪽 칸과 위쪽 값이 모두 현재 칸보다 값이 작을 경우, 왼쪽이나 위쪽으로 이동하지 않고 왼쪽 위 대각선으로 이동해야 함에 주의해야 한다.
그렇지 않으면 위 그림에서 (2, 4)에서 (2, 1)로 이동하는 것과 같은 움직임을 보이게 되는데, 그렇게 하면 첫 번째 문자열의 C가 두 번째 문자열의 두 개의 C에 모두 대응되어 버리기 때문에 올바르지 않은 LCS 값을 구하게 된다.
하나의 문자열이 중복 대응되는 것을 막기 위해, 해당 칸의 바깥 영역에 도달하려면 왼쪽 위 대각선으로 이동해야 한다.
