Heap

정의

• 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리를 기본으로 한 자료구조이다.
  
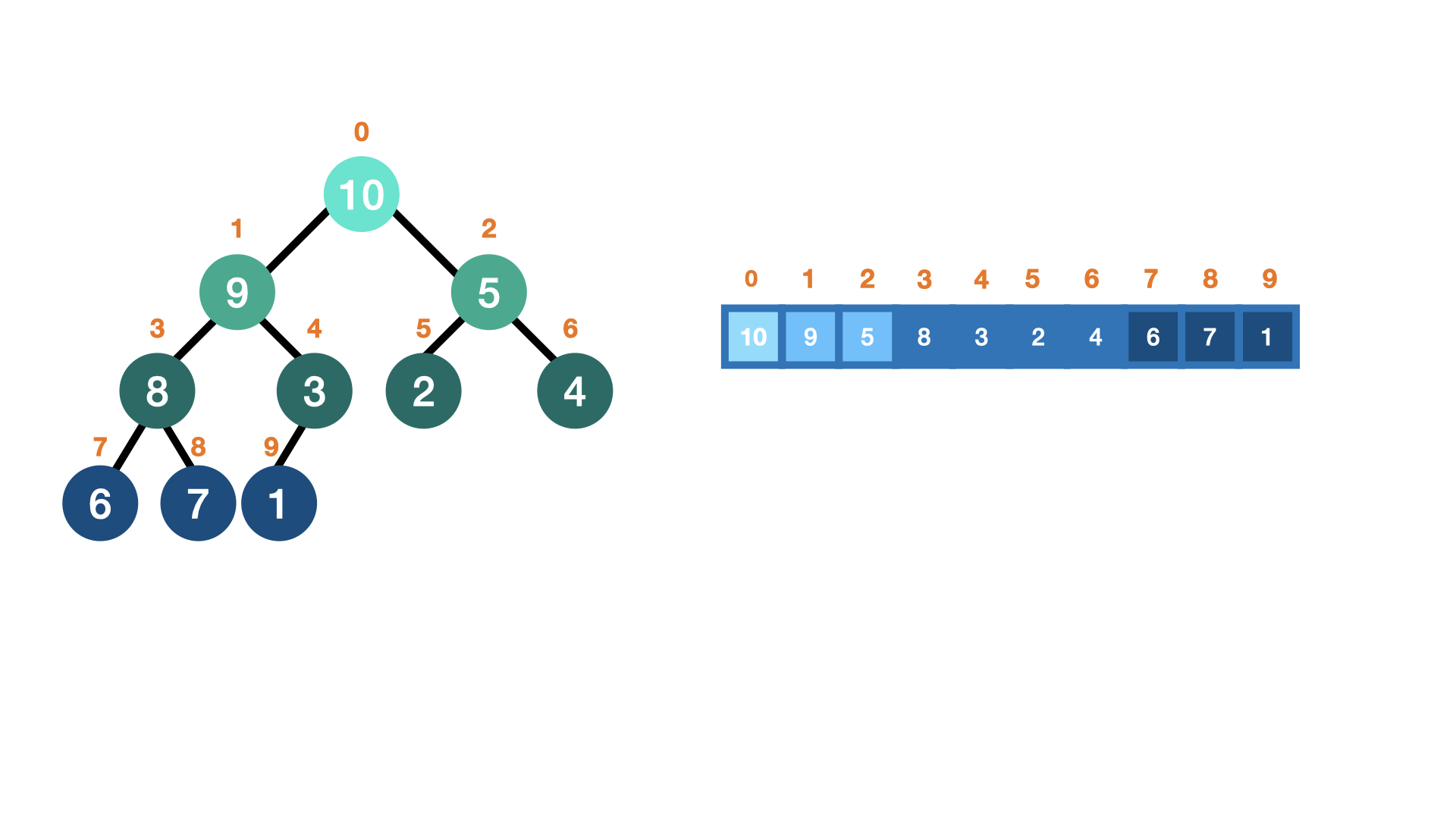
• 완전이진트리 왼쪽 그림을 Max Heap으로 만들면 오른쪽 이미지의 배열로 나타낼 수 있다.

  완전 이진 트리란 부모는 자식을 왼쪽부터 추가하는 모양을 유지하며, 부모가 가질 수 있는 자식의 개수는 최대 2개라는 의미이다.

특징

• 가장 높은 혹은 가장 낮은 우선 순위를 가지는 노드가 항상 root node에 오는 특징을 가지고 있다.
• 이를 응용하면 우선순위 큐 (priority queue)와 같은 자료형을 구현할 수 있다.

종류

• Min Heap: 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰 힙
• Max Heap: 부모 노드의 키 값이 자식 노드의 키 값보다 항상 작은 힙

주의할 점

• 키 값 대소관계는 오로지 부모 노드와 자식 노드 간에만 성립한다.
• 특히 형제 사이에는 대소 관계는 일정하지 않다.
  
  

구현

아래에서 예로 드는 것은 모두 Max Heap을 기준으로 한다.

힙을 배열로

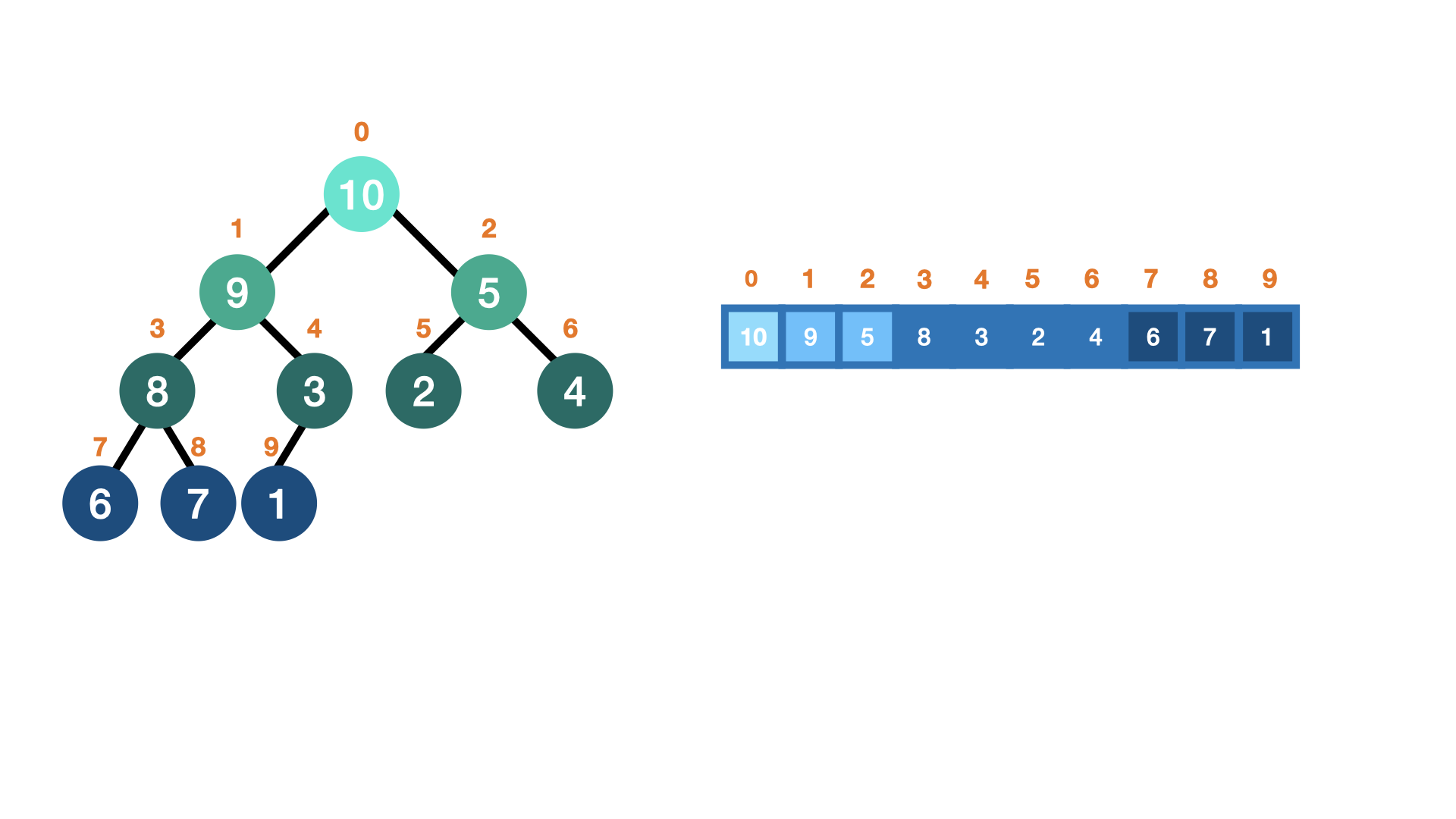
• 부모는 ( index-1 ) / 2 (왼쪽 자식 기준)
• 왼쪽 자식은 index * 2 + 1
• 오른쪽 자식은 index * 2 + 2

삽입 후 힙 상태 유지하기

• 위의 heap에 16을 추가한다고 가정해보자.
  

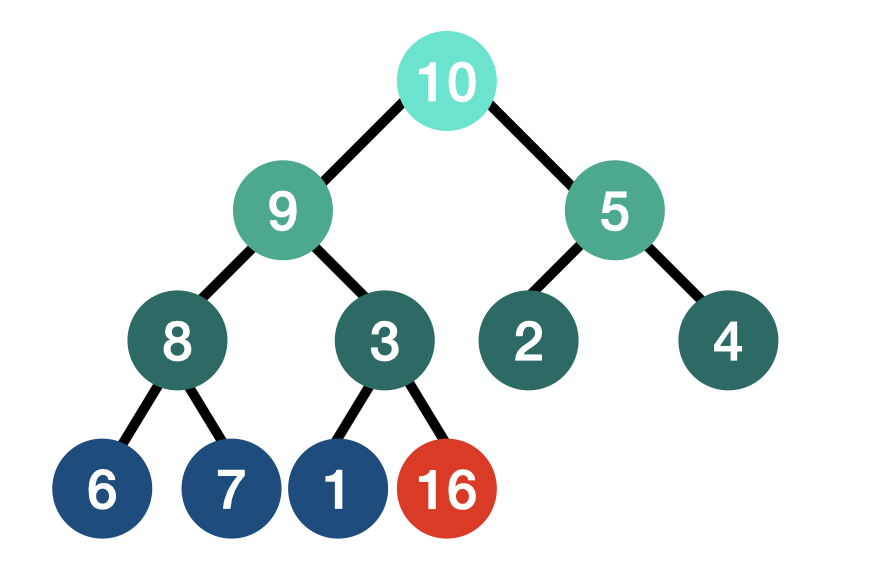
1. 제일 마지막 node에 16을 추가한다.
   
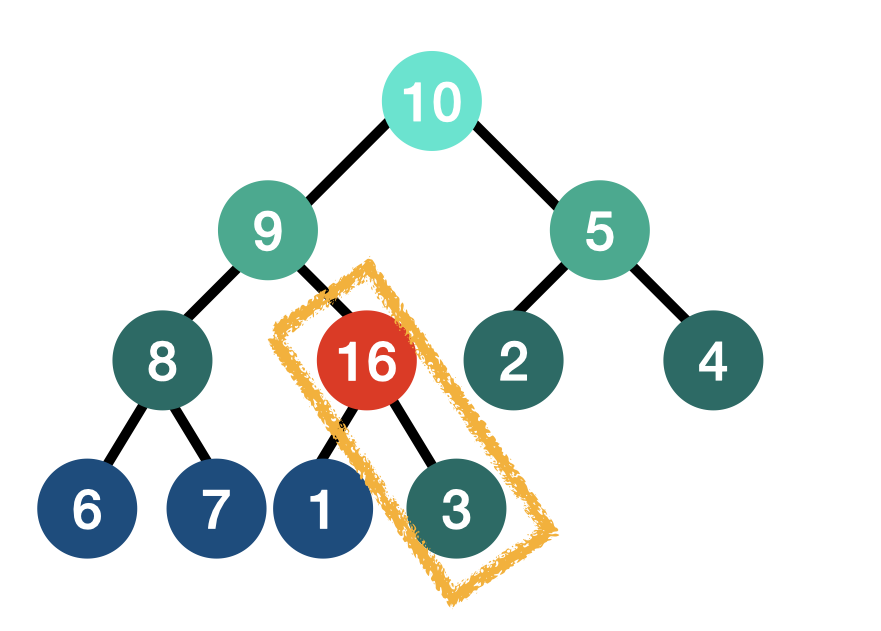
2. 부모 노드와 값을 비교한다. 16이 부모 노드의 값인 3보다 크기 때문에 16이 부모 노드가 되고 3이 자식 노드가 되어야한다.
3. 16과 3의 노드 값을 교환한다.
   
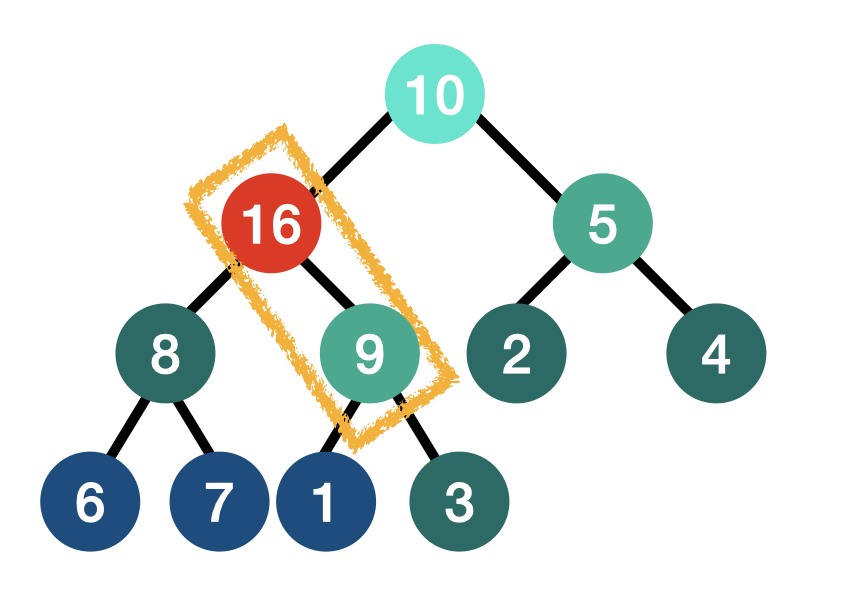
4. 같은 과정을 반복한다.
   

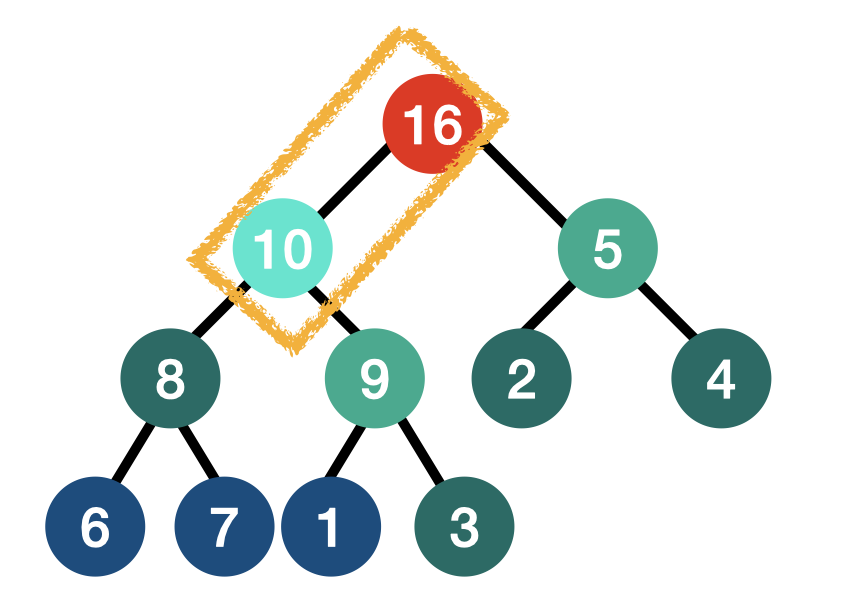
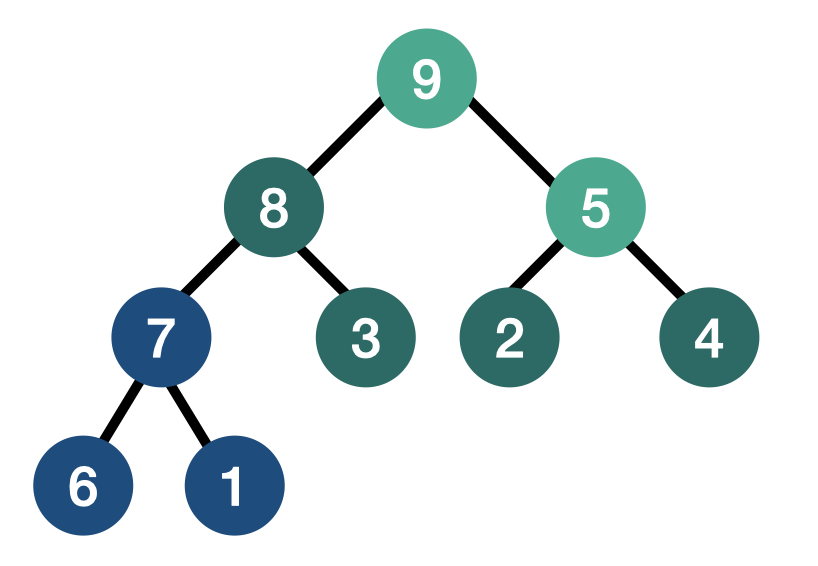
루트 삭제 후 힙 상태 유지하기

1. 루트(10)의 위치를 제일 마지막 노드(1)의 위치와 바꾼뒤, 마지막 노드에 있는 루트의 값 10을 삭제한다.
   
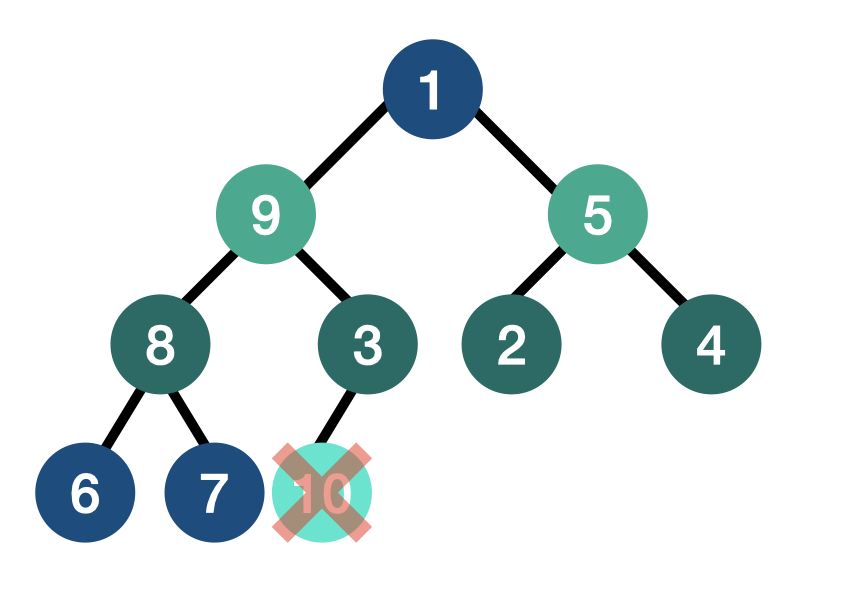
2. 현재 루트 노드에 위치해 있는 1은 자식 노드 중 자신의 값 1보다 큰 값을 가지는 노드와 자리를 바꾸며 아래쪽으로 내려가는 작업을 반복한다. 5와 9는 모두 1보다 크지만, Max Heap이므로 둘 중에서는 제일 큰 값 9와 위치를 바꾼다.
   
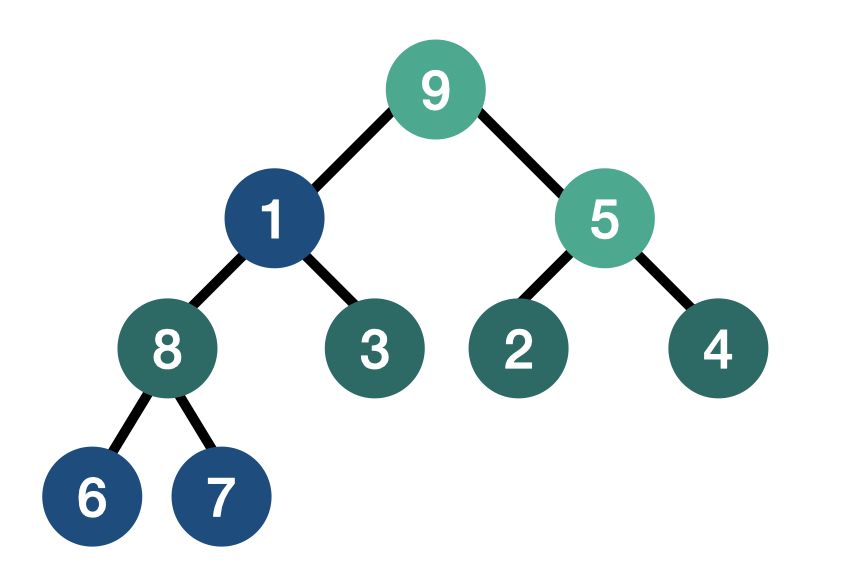
3. 다음 자식 노드의 값 3과 8 모두 1보다 크지만, 8이 제일 크므로 부모 노드의 1의 위치와 8의 위치를 바꾼다.
   
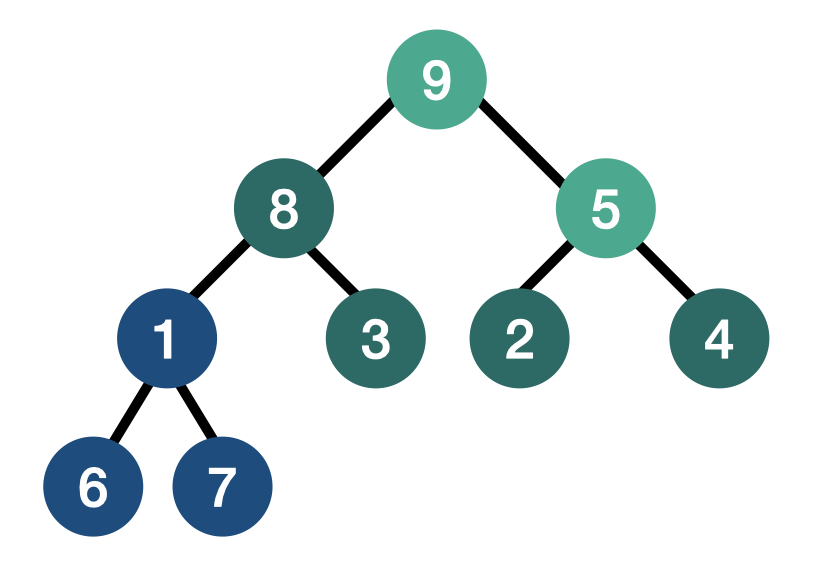
4. 이떄 자식 노드의 값이 작거나 leaf node에 다다르면 작업을 종료한다.
   

Reference

• 힙(자료구조) wiki
• 자료구조와 함께 배우는 알고리즘 입문 자바편
• Data Structures: Heaps