백준 소수 구하기

소수는 1보다 큰 수중에서 자기 자신과 1만을 공약수로 가지는 수이다.

이것을 구하는 여러가지 방법이 있는데.

소수를 판별하고자 하는 수를 num이라고 하면

1. 2부터 num - 1 값까지 중에서 num과 나눠지는 값이 있으면 소수 X (timecomplexity = O(N))

2. 2 부터 루트(num)까지 중에서 num과 나눠지는 값이 있으면 소수 X (timecomplexity = O(루트(N)) ==> 수학 공식 필요

1 ~ N까지의 숫자 중에서 소수인 모든 숫자를 구하는 문제에서

1번째 방법을 사용하면 timecomplexity = O(N N)
2번째 방법을 사용하면 timecomplexity = O(N 루트(N))

에라토스테네스의 채를 이용한 풀이를 사용하면
==> 2부터시작해서 소수의 배수인 수들을 삭제해 나가는것(배수인 수는 소수가 아니므로)
코드 :

		for(int i = 2; i <= B; i++) {
			if(pm[i] == true) {
				for(int j = i*2 ; j <= B; j += i)
					pm[j] = false;
			}
		}

timecomplexity = O(N * lglg(N))

예시:
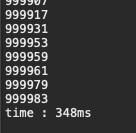
1~ 99999 까지의 숫자중 소수를 찾는 문제

1번을 사용했을 때 O(N N)

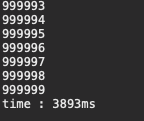
2번을 사용했을 때 O( N 루트(N) )

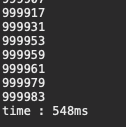
3번을 사용했을 때 O( N * lglgN)