알고리즘 :: 백준 :: Bruteforce :: 1248 :: 맞춰봐

문제

문제링크

문제접근

문제 이해

• 문제가 상당히 길다. 장문의 문제는 수험생에게 혼란을 주기 위해서다.
• 이 문제는 마지막 문단을 제외한 모든 정보가 쓸데없다.
  1. 규현이가 쓴 N개의 수는 A[]배열로 표현한다.
  2. 규현이는 -10부터 10까지의 정수만 알고있다.
  3. S[i][j]는 A[]의 i부터 j까지의 구간합의 부호를 의미한다.
• 정리하면, 주어진 S[][] 을 보고 N개의 수를 역추적하는 문제다.

풀이과정

• 풀이과정은 세 가지 있다.
  1. N개의 칸 각각에 들어갈 수 있는 수 k는 $-10 \leq k \leq 10$ 이다. 따라서 과거 <N과 M> 문제에서 했듯이 모든 경우의 수를 재귀를 이용해서 탐색한다. → $O(21^N)$ 풀이
  2. i번째에 들어갈 수의 부호는 S[i][i]를 보면 알 수 있다는 점에서 탐색 범위를 $-10 \leq k \leq 10$ 에서 $1 \leq k \leq 10$ 으로 절반 줄이고, 부호를 곱하는 방법을 사용한다. → $O(10^N)$ 풀이
  3. i번째에 들어갈 수가 정당한지 판단한다. i번째에 들어갈 수는 S[i][i], S[i-1][i], ... , S[0][i]에 주어진 부호를 모두 만족해야만 한다. 이를 판단하는 check() 함수를 만들어서 만족하는 k만 i번째 수에 넣는다. → $\leq O(10^N)$ 풀이, Backtracking
• 위 세 가지 풀이 중 1, 2번 풀이는 당연히 TLE가 발생한다. 이 문제는 전형적인 backtracking 문제로, 탐색이 불필요한 (S[][]배열의 부호를 만족하지 않는 경우) 경우를 의도적으로 스킵해야만 AC가 가능하다.
  
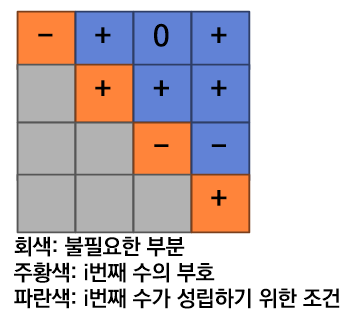
• S[i][i]는 i번째 올 숫자의 부호를 의미한다. (주황색)
• i번째 올 숫자는 해당 열 (파란색)의 모든 조건을 만족해야한다.
  • 예를 들어 -2, 5 라는 숫자를 이미 골랐고 (i=0, i=1), 이제 i = 2번째 숫자를 골라야 한다고 생각해보자.
  • S[2][2]가 -인 것을 보아하니, 음수임을 알 수 있다.
  • for(int num = 1; num <= 10; ++num) a[i] = (부호) * num;
  • 고정을 시켰으니 이제 a[i]가 유효한 수인지 판단한다.
  • 예를 들어 a[2] = -2일 때, a[2] + a[1] = 3이고 S[1][2] = '+'이므로 성립함을 확인할 수 있다.
  • 그리고 a[2] + a[1] + a[0] = 1이고 S[0][2] = 0이므로 성립하지 않음을 확인할 수 있다. 따라서 a[2]는 -2가 될 수 없다.

코드

#include <iostream>
#include <cstdlib>
using namespace std;

int N, s[10][10], a[10];
bool check(int idx) {
	int sum = 0;
	for (int i = idx; i >= 0; --i) {
		sum += a[i];
		char c = ((sum < 0) ? '-' : ((sum == 0) ? '0' : '+'));
		if (c != s[i][idx]) return false;
	}
	return true;
}
void solve(int idx) {
	if (idx == N) {
		for (int i = 0; i < N; ++i) cout << a[i] << ' '; 
		exit(0);
	}
	int sign = (s[idx][idx] == '-') ? -1 : 1;
	for (int num = 0; num <= 10; ++num) {
		a[idx] = sign * num;
		if (check(idx)) solve(idx + 1);
	}
}
int main() {
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin >> N;
        char ch;
	for (int y = 0; y < N; ++y)
		for (int x = y; x < N; ++x) { cin >> ch; s[y][x] = ch; }
	solve(0); 
}

결과