알고리즘 :: 백준 :: Bruteforce :: 13460 :: 구슬 탈출 2

문제

문제접근

문제 이해

• 상, 하, 좌, 우로 구슬을 굴려서 빨간 구슬만 구멍으로 내보내는 최소 회수를 구하는 문제입니다.

• 정말정말 까다로운 문제였습니다. 결국 시간 내에 풀지 못했습니다. 배울 점이 참 많은 문제입니다.

• 주요 조건은 다음과 같습니다.

  1. 공은 동시에 움직입니다.

     • 시뮬레이션 또는 bruteforce 유형 문제에서 종종 나오는 동시성 문제입니다.

     • PS에서는 동시성을 구현할 수 없습니다. 그러므로 반드시 검사 후 진행으로 이해합시다.

       (i.e. 동시에 빨간구슬, 파란구슬을 움직인다 = 빨간구슬 움직일 수 있는지 여부 검사, 좌표 확인하기 + 파란구슬 움직일 수 있는 지 여부 검사, 좌표 확인하기 + 움직이기)

  2. 가장 바깥 행과 열은 모두 벽으로 막혀있습니다.

     • 움직일 때 구슬이 범위 바깥으로 나갔는지 검사할 필요가 없습니다.

  3. 빨간 구슬과 파란 구슬은 동시에 같은 칸에 있을 수 없습니다.

     • 서로 겹칠 수 없음을 의미합니다.

  4. 빨간 구슬과 파란 구슬이 동시에 구멍에 빠지면 실패입니다.

     • 기울였을 때 빨간 구슬과 파란 구슬이 구멍에 빠지는지 flag로 검사해야 합니다.

  5. 시뮬레이션 종료 조건은 '더 이상 구슬이 움직이지 않을 때' 입니다.

     • 기울이고 난 뒤 두 구슬의 좌표가 기울이기 전과 동일하면 시뮬레이션을 종료합니다.

  6. 10번 이하로 빨간 구슬을 빼낼 수 없으면 -1을 출력합니다.

해결 과정

고려할 경우의 수 줄이기

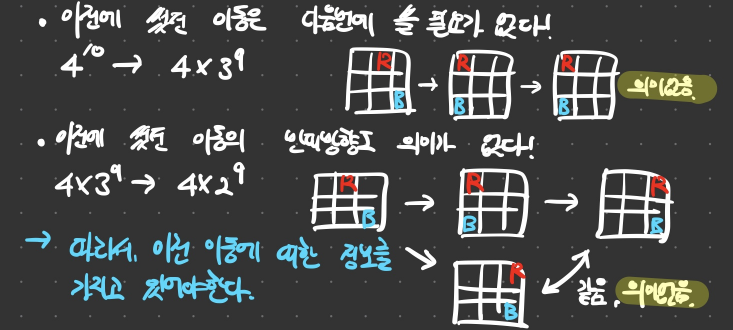
• 상, 하, 좌, 우 네 가지 방향을 모두 고려한다면 10번 이동하므로 $4^{10} = 1,048,576$개 경우를 탐색해야 합니다.
• 하지만, 위 그림처럼 한 번 기울인 방향으로는 다음 번에 다시 기울여도 의미가 없습니다.
• 또한, 한 번 기울인 방향의 반대방향으로 다음 번에 기울여도 의미가 없습니다.
• 따라서 첫 번째 경우는 4가지 경우, 그 다음부터는 2가지 방향만 고려하면 됩니다.
• 결국 $4 \times 2^9 = 324$ 개만 고려하면 됩니다.

방향 표현하기

• 일반적으로 저는 이런 문제를 풀 때, 재귀함수를 사용해서 상, 하, 좌, 우로 기울이는 경우를 처리합니다.
• 하지만, 이 문제는 조금 독특한 해결방법을 사용해볼 수 있습니다.
• 상, 하, 좌, 우 방향을 각각 숫자에 대응하면 0, 1, 2, 3으로 4진법으로 표현할 수 있습니다.
• 10진법을 N진법으로 바꾸는 방법은 N으로 계속 나눈 뒤 뒤집어주면 됩니다.
  • (102를 4진법으로 바꾸면, 102 % 4 = 25...2, 25 % 4 = 6...1, 6 % 4 = 1...2, $2112$ 뒤집기 $2112(4)$ 입니다.)
  • 아이고 하필이면 예로 든 숫자가 뒤집어도 같은 숫자네요...ㅎㅎ
• 0부터 $4^{10} = 2^{20} = 1 << 20$ 까지 모든 경우에 대해 4진법으로 변환한 뒤 연속해서 같은 방향은 없는지, 연속해서 서로 반대 방향은 없는지 검사한 뒤 bruteforce를 수행합니다.

예외 고려하기

• 이 문제는 한 번에 한 칸씩 움직이는 게 아니라 한 번에 여러 칸을 움직이게 됩니다.

• 만일 구슬이 하나고, 서로 겹쳐도 된다는 조건이 있었다면 간단했겠지만 다음과 까다로운 반례가 있습니다.

  

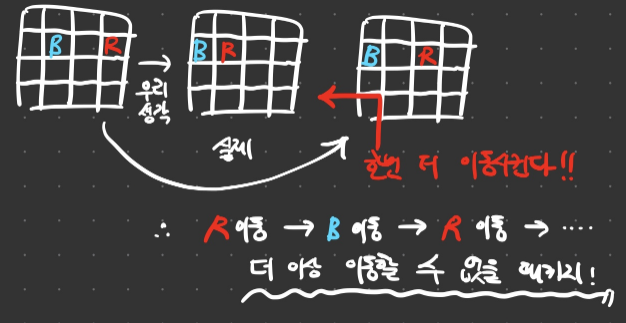
  • 위 그림의 왼쪽 그림을 왼쪽으로 기울인다면 가운데 그림처럼 될 것 같지만 실제로는 그렇지 않습니다.
  • 두 구슬은 동시에 움직일 수 없기 때문에 필연적으로 둘 중 하나가 먼저 움직이게 됩니다.
    위 그림에서는 빨간 구슬이 먼저 움직이고 파란 구슬이 나중에 움직이는 경우입니다.
  • 이때 파란 구슬에 막혀 빨간 구슬은 2행 3열에 멈추게 됩니다.
  • 이 문제를 해결하기 위해서는 더 이상 진행이 불가능할 때까지 계속 움직이면 됩니다.
  • 네 맞습니다. 더 이상 진행이 불가능한 것은 프로그램 종료 조건입니다.
  • 바로 이 반례 때문에 일반적인 방법처럼 재귀를 사용할 수가 없었습니다.
    이 반례가 아니라면 한 번씩 이동한 뒤에 cnt -> cnt + 1로 다음 재귀를 호출하면 됐겠지만, 이 반례를 처리할 수 없었기 때문에 비트마스크 및 4진법 표현으로 아예 10개 방향만 고려하는 것입니다.
  • 이 부분이 이 문제의 가장 어려운 부분이고 핵심입니다!!!

코드

#include <iostream>
#include <vector>
#pragma GCC optimize("O3")
#pragma GCC optimize("Ofast")
#pragma GCC optimize("unroll-loops")
using namespace std;

int N, M;
const int LIMIT = 100;
const int d[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};

// 10진수 num을 4진수로 변환함.
vector<int> dec2Quat(int num) {
	vector<int> base4(LIMIT);
	for (int i = 0; i < LIMIT; ++i)
		base4[i] = (num & 3), num >>= 2;
	return base4;	// 뒤집어 줄 필요없음.
}

bool isValid(const vector<int>& dir) {
	// 연속해서 같은 방향 혹은 반대 방향이면 false
	for (int i = 0; i + 1 < dir.size(); ++i) {
		if (dir[i] == dir[i + 1]) return false;
		if (dir[i] == 0 && dir[i + 1] == 1) return false;
		if (dir[i] == 1 && dir[i + 1] == 0) return false;
		if (dir[i] == 2 && dir[i + 1] == 3) return false;
		if (dir[i] == 3 && dir[i + 1] == 2) return false;
	}
	return true;
}

pair<bool, bool> moveBall(vector<string> &m, int dir, int &y, int &x) {
	// 이미 구슬이 구멍으로 빠졌다면 처리해주지 않고 리턴.
	if (m[y][x] == '.') return {false, false};
	bool moved = false;
	while (true) {
		int ny = y + d[dir][0], nx = x + d[dir][1];
		if (m[ny][nx] == '#') return {moved, false};
		if (m[ny][nx] == 'R' || m[ny][nx] == 'B') return {moved, false};
		if (m[ny][nx] == '.') {
			swap(m[ny][nx], m[y][x]);
			y = ny, x = nx;
			moved = true;
		} else {
			m[y][x] = '.';
			moved = true;
			return {moved, true};
		}
	}
	return {false, false};
}

int go(vector<string> m, const vector<int>& dirs) {
	int holeY, holeX, redY, redX, blueY, blueX;
	for (int y = 0; y < N; ++y)
		for (int x = 0; x < M; ++x) {
			if (m[y][x] == 'O') holeY = y, holeX = x;
			else if (m[y][x] == 'R') redY = y, redX = x;
			else if (m[y][x] == 'B') blueY = y, blueX = x;
		}
	int ret = 0;
	for (int dir : dirs) {
		ret++;
		bool redGoalFlag = false, blueGoalFlag = false;
		while (true) {
			auto redResult = moveBall(m, dir, redY, redX);
			auto blueResult = moveBall(m, dir, blueY, blueX);
			bool redMove = redResult.first, blueMove = blueResult.first;
			if (!redMove && !blueMove) break;	// 둘 다 움직일 수 없다면 시뮬레이션 종료
			if (redResult.second) redGoalFlag = true;
			if (blueResult.second) blueGoalFlag = true;
		}
		// 파란구슬이 구멍으로 들어갔다면 오류, 아니라면 답 반환.
		if (blueGoalFlag) return -1;
		if (redGoalFlag) return ret;
	}
	return -1;
}

int main() {
	ios::sync_with_stdio(false), cin.tie(NULL);
	cin >> N >> M;
	vector<string> map(N);
	for (int i = 0; i < N; ++i) cin >> map[i];
	
	int ans = -1;
	vector<int> ansDirs;
	for (int i = 0; i < (1 << (LIMIT * 2)); ++i) { // 4^10 가지 경우의 수
		vector<int> dirs = dec2Quat(i);	// 방향 정보를 받아온다.
		if (!isValid(dirs)) continue;	// 유효한 방향인지 확인한다.
		int result = go(map, dirs);
		if (result == -1) continue;
		if (ans == -1 || ans > result) {
			ans = result;
			ansDirs = dirs;
		}
	}
	cout << ans << '\n';
	if (ans != -1) {
		for (int i = 0; i < ans; ++i) {
			if (ansDirs[i] == 0) cout << 'R';
			else if (ansDirs[i] == 1) cout << 'L';
			else if (ansDirs[i] == 2) cout << 'D';
			else cout << 'U';	
		} cout << '\n';	
	}
}

결과