알고리즘 :: 백준 :: DFS, BFS :: 16947 :: 서울 지하철 2호선

문제

지하철 2호선에는 51개의 역이 있고, 역과 역 사이를 연결하는 구간이 51개 있다. 즉, 정점이 51개이고, 양방향 간선이 51개인 그래프로 나타낼 수 있다. 2호선은 순환선 1개와 2개의 지선으로 이루어져 있다. 한 역에서 출발해서 계속 가면 다시 출발한 역으로 돌아올 수 있는 노선을 순환선이라고 한다. 지선은 순환선에 속하는 한 역에서 시작하는 트리 형태의 노선이다.
두 역(정점) 사이의 거리는 지나야 하는 구간(간선)의 개수이다. 역 A와 순환선 사이의 거리는 A와 순환선에 속하는 역 사이의 거리 중 최솟값이다. 지하철 2호선과 같은 형태의 노선도가 주어졌을 때, 각 역과 순환선 사이의 거리를 구해보자.

문제접근

• 순환선(사이클)이 한 개 존재하고 지선은 0개 이상 존재한다.
• DFS, BFS 특성을 고려하면, 사이클을 구할 때는 DFS를 사용하는 것이 유리함 알 수 있으며, 지선상에 있는 역과 순환선으로부터의 거리는 BFS를 사용하는 것이 유리함을 알 수 있다.

순환선(사이클) 구하는 법

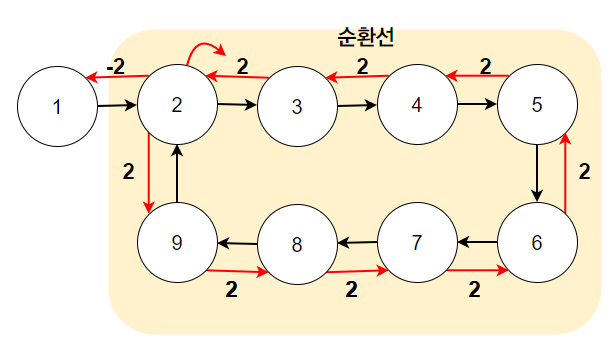
• 1번 노드부터 DFS를 출발한다고 가정하자.
• 1->2->3->...->9->2로 DFS가 돌 것이다. 2번 노드는 재방문하게 되는데, 이때 자신의 번호 2를 반환한다.
• 재귀 반환에 따라 지금까지 방문한 모든 정점에 2를 반환하게 된다.
• 이때, 2번노드와 반환값 2가 동일하므로, "사이클의 시작지점으로 돌아왔구나!"라고 알 수 있다.
• 그러므로, 1번노드는 사이클을 찾았으나, 사이클에 포함되지 않는 정점임을 기록해주기 위해 -2를 반환한다.

지선(거리) 구하는 법

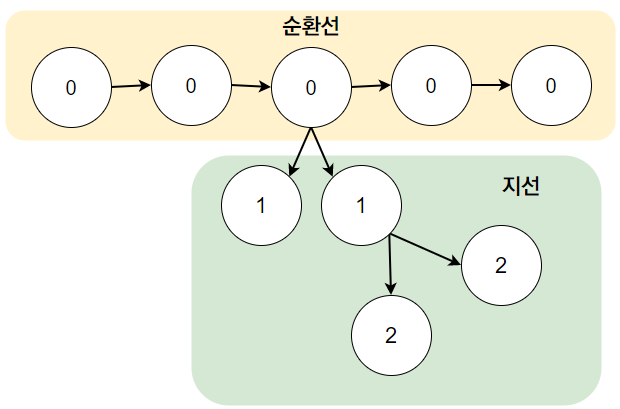
• 모든 순환선으로부터 BFS를 수행한다.
• 순환선에 포함된 모든 역은 거리가 0으로 초기화된다.
• 순환선에 포함된 어떤 역으로부터 BFS를 수행하면, 그 역과 연결된 지선들의 거리를 계산할 수 있다.

코드

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

vector<int> metro[3000];
int N, check[3000], dist[3000];

// cv: current vertex number, pv: prev, nv: next
// -2: 사이클을 찾았으나 해당 정점은 사이클에 포함되지 않음
// -1: 사이클을 찾지 못한 경우
// 0 이상: 사이클을 찾았으며 시작 정점의 번호가 저장됨.
int dfs(int cv, int pv) {	// 사이클(순환선)을 DFS로 구한다.
	// 기저: 이미 방문한 점이면 사이클을 찾은 것이다.
	if (check[cv] == 1) return cv;
	check[cv] = 1;

	for (const int nv : metro[cv]) {
		if (nv == pv) continue;	// 다시 이전 정점으로 돌아가는 경우 필요 X.
		int result = dfs(nv, cv);
		if (result == -2) return -2;
		if (result >= 0) {	// 0 이상일 경우 사이클에 포함되는 정점이다.
			check[cv] = 2;	// 해당 정점은 사이클에 포함되는 정점임을 기록한다.
			return (cv == result) ? -2 : result;	// 사이클 시작점부터는 -2로 기록.
		}
	}
	return -1;
}

void bfs() {	// 사이클에 포함되지 않은 정점들의 거리를 BFS로 구한다.
	queue<int> q;
	for (int i = 0; i < N; ++i) {
		if (check[i] == 2) q.push(i); // 사이클에 포함될 경우 거리 0
		else dist[i] = -1;	// 사이클에 포함 안 될 경우 -1로 초기화
	}
	while (!q.empty()) {	// 모든 사이클 포함 정점에서 시작해서 탐색한다.
		int cv = q.front(); q.pop();
		for (const int nv : metro[cv]) {
			if (dist[nv] == -1) {	// 아직 방문하지 않은 정점인 경우
				q.push(nv);	// 해당 정점을 queue에 넣고
				dist[nv] = dist[cv] + 1;// 거리를 하나 늘려준다.
			}
		}
	}
}

int main() {
	ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
	cin >> N;
	for (int i = 0; i < N; ++i) {
		int s, e;	cin >> s >> e;
		metro[s - 1].push_back(e - 1);
		metro[e - 1].push_back(s - 1);
	}
	dfs(0, -1);
	bfs();
	for (int i = 0; i < N; ++i) cout << dist[i] << ' ';
	cout << '\n';
}

결과