알고리즘 :: 백준 :: Bruteforce :: 1208 :: 부분수열의 합2

문제

N개의 정수로 이루어진 수열이 있을 때, 크기가 양수인 부분수열 중에서 그 수열의 원소를 다 더한 값이 S가 되는 경우의 수를 구하는 프로그램을 작성하시오.

문제접근

https://velog.io/@embeddedjune/알고리즘-백준-Bruteforce-1182-부분수열의-합 문제의 심화버전이다. 다음과 같은 부분이 달라졌다.

1. 요소 개수 N이 20에서 40으로 늘어났다. $2^{40}$은 약 1.1조이므로 더 이상 int 범위로는 풀이할 수 없다.
2. 시간초과가 기존 2초에서 1초로 줄었다. 즉 Bruteforce 방식을 어떻게 효율적으로 만들 것인지 생각해야 한다. 기존 방식으로는 1초내로 풀 수 없다.

• 여기서는 bitset 연산과 MITM(Meet In The Middle) 풀이법과 투 포인터 풀이법 세 가지를 사용해서 문제를 보다 효율적으로 풀어볼 것이다.

1. -7 -3 -2 5 8이라는 수열이 주어졌다면 이 수열을 절반 크기의 두 부분수열로 나눈다. -7 -3 -2와 5 8이 된다.
2. 두 부분수열에서 나올 수 있는 모든 합 조합을 계산하고 외부 배열(앞쪽 부분수열에 대한 저장공간을 front, 뒤쪽 부분수열에 대한 저장공간을 back이라고 명명하자. ) 에 기록한다.
   • 우리는 앞서 n개에 대한 모든 조합은 $2^n - 1$개 나온다고 했으므로 shift operation을 사용해보자.
   • 1 << (N / 2);는 $2^{n/2}$를 의미한다.
3. front와 back에 각 부분수열에서 만들어지는 모든 합이 기록됐다면, front는 오름차순으로, back은 내림차순으로 정렬한다.

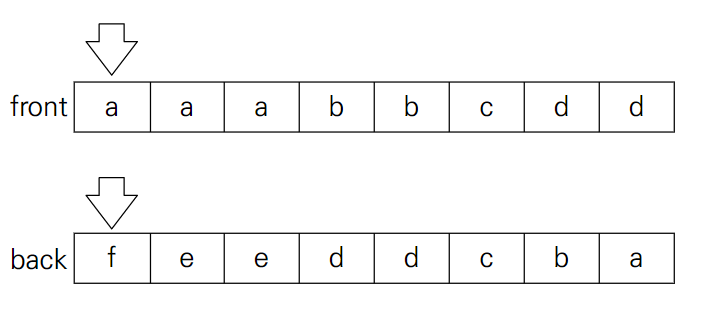
4. 우리가 할 일은 front의 포인터 frontIdx와 back의 포인터 backIdx를 해당 포인터들이 가리키는 요소값끼리 비교해서 증감시켜주는 일이다. 세 가지 경우로 나눌 수 있다.
   • *frontIdx 와 *back을 더한 값이 S인 경우
     • 우리가 원하는 조합을 찾은 경우이므로 frontIdx와 backIdx를 조정하면서 *frontIdx 또는 *backIdx와 값이 똑같은 요소 갯수를 찾고 두 갯수를 곱한다.
     • 왜냐하면 값이 똑같은 요소들 끼리는 똑같이 S가 나올 것이기 때문이다.
     • 잘 이해가 가지 않는다면, a, a, a와 b, b, b가 있다고 생각해보자. a + b가 S라면, S가 나오는 경우의 수는 a 3개 * b 3개 = 9개이다.
   • *frontIdx 와 *back을 더한 값이 S보다 작은 경우
     • frontIdx값을 한 칸 오른쪽으로 옮겨준다. 왜냐하면 backIdx값을 한 칸 오른쪽으로 옮겨주면 방금 더한 값보다 더 작아질 것이기 때문에 값을 증가시켜주기 위해서는 frontIdx를 옮겨주는 것이 옳다.
   • *frontIdx 와 *back을 더한 값이 S보다 큰 경우
     • backIdx값을 한 칸 오른쪽으로 옮겨준다. 왜냐하면 frontIdx값을 한 칸 오른쪽으로 옮겨주면 방금 더한 값보다 더 커질 것이기 때문에 값을 감소시켜주기 위해서는 backIdx를 옮겨주는 것이 옳다.
5. 주의할 점이 있는데, 만일 주어진 S == 0이라면, 위 과정을 거치면서 0이 중복 계산된다. 따라서 마지막 계산 결과에서 1을 빼줘야 한다.

코드

#include <iostream>
#include <vector>
#include <algorithm>
#include <functional>
using namespace std;

int N, S;
vector<int> vec;

long long solve() {
    int half = N / 2;
    int frontSize = (1 << (N - half)), backSize = (1 << half);
    vector<int> front(frontSize), back(backSize);

    for (int i = 0; i < frontSize; ++i)
        for (int j = 0; j < N - half; ++j)
            if (i & (1 << j)) front[i] += vec[j];
    for (int i = 0; i < backSize; ++i)
        for (int j = 0; j < half; ++j)
            if (i & (1 << j)) back[i] += vec[j + (N - half)];

    sort(begin(front), end(front));
    sort(begin(back), end(back), greater<int>());

    int frontIdx = 0, backIdx = 0;
    long long ret = 0;

    while (frontIdx < frontSize && backIdx < backSize) {
        int caseSelector = front[frontIdx] + back[backIdx];
        if (caseSelector == S) {
            long long countFront = 1, countBack = 1;
            frontIdx++; backIdx++;
            
            while (frontIdx < frontSize && front[frontIdx] == front[frontIdx - 1]) {
                frontIdx++;
                countFront++;
            }
            while (backIdx < backSize && back[backIdx] == back[backIdx - 1]) {
                backIdx++;
                countBack++;
            }
            ret += (countFront * countBack);
        } 
        else if (caseSelector < S) frontIdx++;
        else if (caseSelector > S) backIdx++;
    }
    return (S == 0) ? ret - 1 : ret;
}

int main() {
    ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
    cin >> N >> S;
    vec = vector<int>(N);
    for (int i = 0; i < N; ++i) cin >> vec[i];

    cout << solve() << '\n';
}

• long long을 사용하지 않으면 오버플로우가 나서 올바른 값을 찾을 수 없다.
• front와 back을 만드는 과정에서 bitset 연산을 사용했다.
  i & (1 << j)가 의미하는 바는 다음과 같다.
  
• 주어지는 N이 5일 경우 front의 크기는 1 << N / 2 = 8이다. 따라서 인덱스 i는 0부터 7까지 증가할 것이다. j는 0부터 i까지 증가하며 i를 2진법으로 나타냈을 때 1이 있는 곳마다 if문으로 들어가서 합을 계산하게 된다.

결과