문제
문제접근
문제 이해
- 정말 어려웠던 문제였습니다. 이 문제는 두 가지가 어렵습니다.
- 문제 이해하는 것이 어렵습니다.
- PS 경험이 적은경우, 시계 방향이라는 표현이 애매모호합니다.
- 글과 그림을 봐도 어떻게 이런 그림이 나오는지 이해하기 힘듭니다.
- 드래곤 커브를 어떻게 구현할지 생각하기 어렵습니다.
- 다행히 문제에 어느정도 힌트가 나와 있었습니다. (
시점, 방향, 세대) - 저는 처음에는 구조체를 이용했고, 두 번째 풀 때는 방향 정보만 이용했습니다.
- 다행히 문제에 어느정도 힌트가 나와 있었습니다. (
- 문제 이해하는 것이 어렵습니다.
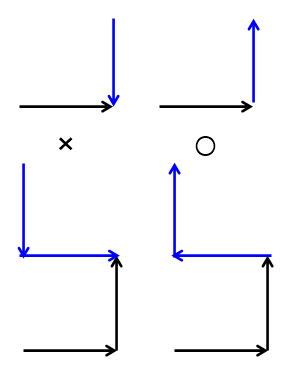
- 문제 조건에 따르면 이전 세대의 선을 시계 방향으로 회전해서 붙힌다고 돼있습니다.
따라서 문제 조건에 따르면 위 그림의 왼쪽 그림이 맞습니다. - 하지만, 드래곤 커브는 시점과 방향으로 정의되므로 방향이 반대로 돼야합니다.
첫 번째 방법 - 구조체 활용
-
저는 구현이 어려운 경우, 효율적인 풀이를 신경쓰지 않고 문제의 모든 조건을 그대로 구현하려고 합니다.
-
구조체를 사용하는 방법은 문제에서 언급된 드래곤 커브의 정의를 그대로 따라하는 것입니다.
struct Line { int y, x, d; }; struct Curve { Line lines[1025]; int gen;};- 드래곤 커브는 최대 1,024개의 선을 가지게 됩니다.
- 각 선은 시점
(y, x)와 방향d로 구성됩니다. - 드래곤 커브는 최대 20개 있을 수 있으므로
Curve curve[20]일차원 배열을 만듭니다.
-
구조체를 사용하면 구현이 한결 편해집니다. 하지만 메모리와 속도 면에서는 손해를 봅니다.
-
각 드래곤 커브에 대해 각
generation에 있는 개의 선을 시계 방향으로 바꾸는 등의 처리를 해줘야 하므로 3중 for문을 사용합니다. -
이때 마지막 for문이 코드만 봐서는 햇갈리실 수 있으므로 0번 방향, 3-generation을 예로 설명드리겠습니다.
C++이 아니라C로 짰기 때문에 최대 라인 1,024개를 저장할 수 있는 정적 일차원 배열이Curve구조체에 선언돼있습니다.- for문에는
i와j가 있습니다. - 각 세대는 개 선으로 구성돼있습니다. 따라서
i는 쉬프트 연산을 사용해서 초기화합니다.
쉬프트 연산은0을 표현할 수 없으므로Curve구조체의Line배열은1번 인덱스부터 시작합니다. - 새로운 세대의 선은 이전 세대의 선으로부터 만들어집니다.
이때i는Line배열의 왼쪽으로 이동하며,j는 오른쪽으로 이동하며 새로운 선과 방향을 만듭니다. Line구조체는시점과 방향정보만 가지고 있으므로종점을 알기 위해 계산이 필요합니다.종점은시점에 방향을 더해주면 구할 수 있습니다.
이렇게 구한종점은 새로운 선의시점입니다.- 이제 지도에 표시하기 위해 새로운 선의
종점을 구해야 합니다.
이 역시 방금과 마찬가지로 방향을 더해서 구합니다. - 지도에 표시해줍니다.
두 번째 방법 - 개선된 방법
-
첫 번째 방법을 어느정도 이해하신 분께서는 아시겠지만, 사실 구조체를 쓸 필요가 없습니다.
-
모든 방향을 일차원 배열에 저장해둔다면, 시작점으로부터 좌표를 계산할 수 있기 때문입니다.
따라서 중요한 것은 방향 정보입니다.// 목표 gen까지 반복하며 2^g개의 선을 처리합니다. for (int g = 0; g < gen; ++g) for (int l = (1 << g), r = l + 1; l > 0; --l, ++r) dirs[r] = (dirs[l] + 1) % 4; -
첫 번째 방법에서 설명했던 것처럼
l과r을 이용해서 지금까지 만든 선을 가지고 새로운 선들을 만듭니다.
코드
#include <cstdio>
int N, moving[4][2] = {{0, 1}, {-1, 0}, {0, -1}, {1, 0}};
bool map[101][101];
struct Line { int y, x, d; };
struct Curve { Line lines[1025]; int gen;};
Curve curves[20];
int main() {
scanf("%d", &N);
for (int i = 0; i < N; ++i) {
int x, y, d, g;
scanf("%d %d %d %d", &x, &y, &d, &g);
// 입력받은 0-gen 커브 정보를 저장합니다.
curves[i].gen = g;
curves[i].lines[1].x = x;
curves[i].lines[1].y = y;
curves[i].lines[1].d = d;
// 첫 시점과 종점을 기록합니다.
map[y][x] = true;
map[y + moving[d][0]][x + moving[d][1]] = true;
}
// 모든 N개 드래곤 커브에 대해
for (int n = 0; n < N; ++n) {
// 각 드래곤 커브의 0-gen 부터 목표 gen까지
for (int g = 0; g < curves[n].gen; ++g) {
// 2^g 개의 라인에 대해 처리해줍니다.
for (int i = 1 << g, j = i + 1; i > 0; --i, ++j) {
// 시점 정보
int cy = curves[n].lines[j - 1].y;
int cx = curves[n].lines[j - 1].x;
int cd = curves[n].lines[j - 1].d;
int ccd = curves[n].lines[i].d;
// 종점 정보 (새로 생긴 선의 시점이 된다.)
int ny = cy + moving[cd][0];
int nx = cx + moving[cd][1];
int nd = (ccd + 1) % 4;
// 새로 생긴 선의 종점 정보
int nny = ny + moving[nd][0];
int nnx = nx + moving[nd][1];
// 정보 저장 및 지도에 기록.
curves[n].lines[j].y = ny;
curves[n].lines[j].x = nx;
curves[n].lines[j].d = nd;
map[ny][nx] = true;
map[nny][nnx] = true;
}
}
}
int ans = 0;
for (int y = 0; y < 100; ++y)
for (int x = 0; x < 100; ++x)
if (map[y][x] && map[y + 1][x] && map[y][x + 1] && map[y + 1][x + 1]) ans++;
printf("%d", ans);
}개선된 코드
#include <cstdio>
bool map[101][101];
int N, dirs[1025], moving[4][2] = {{0, 1}, {-1, 0}, {0, -1}, {1, 0}};
int main() {
scanf("%d", &N);
int x, y, dir, gen;
// N개의 드래곤 커브를 입력받습니다.
while (N--) {
scanf("%d %d %d %d", &x, &y, &dir, &gen);
// 0-gen의 방향을 저장하고 지도에 기록합니다.
dirs[1] = dir;
map[y][x] = true;
// 목표 gen까지 반복하며 2^g개의 선을 처리합니다.
for (int g = 0; g < gen; ++g)
for (int l = (1 << g), r = l + 1; l > 0; --l, ++r)
dirs[r] = (dirs[l] + 1) % 4;
// 지도에 표시합니다.
for (int i = 1; i <= (1 << gen); ++i) {
y += moving[dirs[i]][0];
x += moving[dirs[i]][1];
map[y][x] = true;
}
}
int ans = 0;
for (int y = 0; y < 100; ++y)
for (int x = 0; x < 100; ++x)
if (map[y][x] && map[y + 1][x] && map[y][x + 1] && map[y + 1][x + 1]) ans++;
printf("%d", ans);
}결과

