알고리즘 :: 이것이 코딩 테스트다 :: 최단거리 :: Q38 :: 정확한 순위

문제

학생들의 성적을 비교한 결과가 주어질 때, 성적 순위를 정확히 알 수 있는 학생은 모두 몇 명인지 계산하는 프로그램을 작성하세요.

문제접근

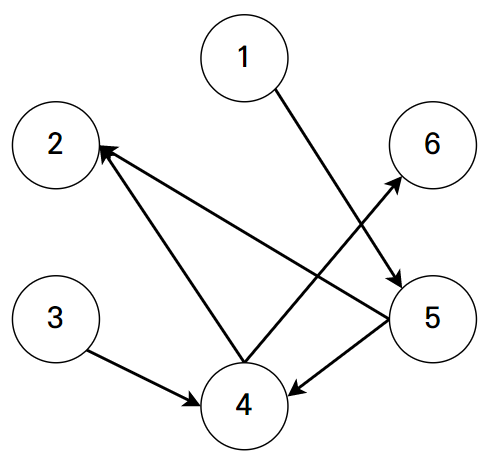
• 4번 학생은 1, 3, 5번 학생이 자신보다 순위가 낮고, 2, 6번 학생이 자신보다 순위가 높기 때문에 전체 3등이라는 것을 확실하게 알 수 있다.
• 두 학생 A와 B 사이의 성적을 비교할 수 있기 위해서는 반드시 어떤 경로를 거치든지 A에서 B 또는 B에서 A로 향하는 경로가 존재해야 한다.
• 따라서 이 문제는, 모든 점에서부터 다른 점까지 갈 수 있는 경로가 존재하는지 알아보는 플로이드 알고리즘 문제이다.
• 모든 점에서부터 다른 점들까지 갈 수 있는 모든 경로를 2차원 배열에 나타낸다.
  만일, 갈 수 없는 경로가 있다면 해당 점은 0또는 INF로 표현이 될 것이다. (초기화하는 사람 맘대로다)
• 플로이드 알고리즘 수행 결과, 모든 점까지 갈 수 있는 경로가 존재하는 정점 개수가 곧 성적 순위를 정확히 알 수 있는 학생의 수다.

코드

#include <iostream>
using namespace std;

static constexpr int INF = 1e9;
static int N, M, students[501][501];

int main() {
    ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
    cin >> N >> M;
    
	// [과정 1]: 전체 그래프 인접 행렬 요소를 INF로 초기화.
    fill(&students[0][0], &students[N][N], INF);
	// [과정 2]: i에서 i로 가는 cost는 0이다.
    for (int i = 1; i <= N; ++i) students[i][i] = 0;
	// [과정 3]: 간선을 입력받는다.
    for (int i = 0; i < M; ++i) {
        int s, e;   cin >> s >> e;
        students[s][e] = 1;
    }
	// [과정 4]: 플로이드 알고리즘 사용
	// s에서 e로 가거나, e에서 s로 가는 방법이 없다면 순위 비교 불가능.
    for (int k = 1; k <= N; ++k)
        for (int s = 1; s <= N; ++s)
            for (int e = 1; e <= N; ++e)
                students[s][e] = min(students[s][e], students[s][k] + students[k][e]);
	// [과정 5]: 플로이드 결과 행렬에서 모든 순위를 알 수 있는 정점 개수를 구한다.
    int answer = 0;
    for (int i = 1; i <= N; ++i) {
        int count = 0;
        for (int j = 1; j <= N; ++j)
            if (students[i][j] != INF || students[j][i] != INF) count++;
        if (count == N) answer++;
    }
    cout << answer << '\n';
}