Chapter 10
Section1:: 서로소 집합(disjoint sets), Union & find 연산
개념
서로소 집합은 중복되는 원소나 교집합이 없게끔 자료를 저장하는 자료구조를 의미한다. 그래프와 연관되는 개념이지만 서로소 집합은 트리 개념(Root-Parent-Child)을 따르는 것이 특징이다.
설명

- N개의 원소(정점)가 있을 때, 처음에는 각 정점을 서로 다른 집합에 넣는다.
- 임의의 간선이 주어질 때 두 정점이 서로 다른 집합에 있다면 begin() 연산으로 같은 집합으로 만들어줍니다.
- 이 과정에서 두 정점의
root를 서로 같게 만들어줍니다. - 이 과정에서 두 정점의
root를 찾기 위해find()연산을 사용한다.
- 이 과정에서 두 정점의
- 이 과정을 M번 반복하면 정점들의
root정보가 고정됩니다.
예시

- 모든 정점을 서로 다른 집합에 넣는다.
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 |
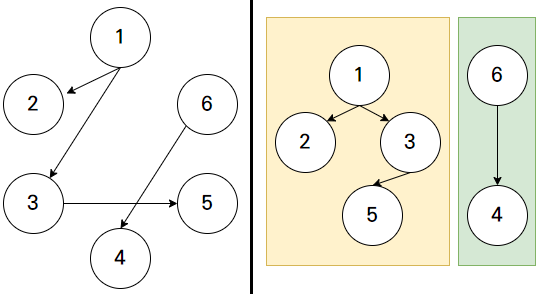
- 간선
(1, 2), (1, 3), (3, 5), (6, 4)가 입력됐다.- 1번 정점과 2번 정점이 서로 다른 집합에 들어가있으므로
union()연산을 수행한다.- 1번 정점의 집합이
1이고, 2번 정점의 집합이2이므로 둘 다 정점 번호와 집합 번호가 같다. 1이2보다 작으므로 (우선순위가 크므로)2를1로 변경한다.- 이제 2번 정점은 1번 정점과 같은 집합이 된다.
- 1번 정점의 집합이
- 1번 정점과 3번 정점이 서로 다른 집합에 들어가있으므로
union()연산을 수행한다.- 1번 정점은
1번 집합에, 3번 정점은3번 집합에 있으므로 둘 다 정점 번호와 집합 번호가 같다. 1이3보다 작으므로 (우선순위가 크므로)2를1로 변경한다.- 이제 3번 정점은 1번 정점과 같은 집합이 된다.
- 1번 정점은
- 3번 정점과 5번 정점이 서로 다른 집합에 들어가있으므로
union()연산을 수행한다.- 3번 정점은
1번 집합에, 5번 정점은5번 집합에 있으므로 3번 정점이 집합 번호와 다르다.find()연산을 해서3번 -> 1번으로 이동한다.- 1번 =
1이므로find()연산을 종료하고1을 반환한다.
1이5보다 작으므로 (우선순위가 크므로)5를1로 변경한다.- 이제 5번 정점은 1번 정점과 같은 집합이 된다.
- 3번 정점은
- 1번 정점과 2번 정점이 서로 다른 집합에 들어가있으므로
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 4 | 1 | 4 |
코드
#include <iostream>
#include <vector>
using namespace std;
// 재귀적으로 따라가면서
int findRoot(vector<int>& parentArr, int x) {
if (parentArr[x] == x) return x;
return parentArr[x] = findRoot(parentArr, parentArr[x]);
}
// 두 정점의 parent 또는 root를 찾고 같은 root(집합)에 소속시킨다.
void unionOperation(vector<int>& parentArr, int lhs, int rhs) {
lhs = findRoot(parentArr, lhs), rhs = findRoot(parentArr, rhs);
parentArr[rhs] = lhs;
}
int main() {
ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
int V, E; cin >> V >> E;
// 정점들의 root(또는 소속집합) 정보를 기록할 parentArr 배열.
vector<int> parentArr(V + 1);
// 모든 정점을 서로 다른 root(집합)에 소속시킨다.
for (int i = 1; i <= V; ++i) parentArr[i] = i;
// 간선을 입력받고 union() 연산을 수행한다.
for (int i = 0; i < E; ++i) {
int s, e; cin >> s >> e;
unionOperation(parentArr, s, e);
}
// [Option]:: 각 정점들의 root 정보를 출력한다.
for (int i = 1; i <= V; ++i)
cout << findRoot(parentArr, i) << '\t';
cout << '\n';
// [Oprtion]:: 각 정점들의 parent 정보를 출력한다.
for (int i = 1; i <= V; ++i)
cout << parentArr[i] << '\t';
cout << '\n';
}Section2:: 크루스칼 알고리즘 (Kruskal algorithm)
개념
크루스칼 알고리즘은 간선에 weight이 존재하는 무방향 그래프에 대해 모든 정점을 연결하면서 간선의 weight합이 최소가 되는 최소 신장 트리를 구하는 알고리즘이다. 시간 복잡도는 이다.
설명

- 좌측 그림과 같은 그래프가 주어질 때, 모든 간선의
weight을 오름차순으로 정렬한다.12 → 18 → 20 → 22 → 24 → 35 → 38 → 41 → 60으로 정렬된다.
- 앞에서부터 간선을 추가하면서 사이클이 생성되는지 검사한다.
- 간선의 두 정점에 대해
find()연산을 통해 서로 같은 root에 포함된다면 사이클이 발생하는 것이다! - 간선의 두 정점에 대해
find()연산을 통해 서로 다른 root에 있다면union()연산을 수행한다.
- 간선의 두 정점에 대해
- MST의 정점의 개수가 일 때, 간선의 개수는 이다.
코드
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int findRoot(vector<int>& parentArr, int x) {
if (parentArr[x] != x) return findRoot(parentArr, parentArr[x]);
return parentArr[x];
}
void unionOperation(vector<int>& parentArr, int lhs, int rhs) {
lhs = findRoot(parentArr, lhs), rhs = findRoot(parentArr, rhs);
(lhs < rhs) ? (parentArr[rhs] = lhs) : (parentArr[lhs] = rhs);
}
int main() {
ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
int V, E; cin >> V >> E;
// 정점들의 root(또는 소속집합) 정보를 기록할 parentArr 배열.
// 모든 정점을 서로 다른 root(집합)에 소속시킨다.
vector<int> parentArr(V + 1);
for (int i = 1; i <= V; ++i) parentArr[i] = i;
// 간선을 입력받고 mst 배열에 넣는다.
vector<pair<int, pair<int, int>>> mst;
for (int i = 0; i < E; ++i) {
int s, e, w; cin >> s >> e >> w;
mst.push_back({w, {s, e}});
}
// 간선의 weight을 오름차순으로 정렬한다.
sort(begin(mst), end(mst));
cout << '\n';
for (const auto& itr : mst)
cout << '(' << itr.second.first << ", " << itr.second.second << ") = " << itr.first << '\n';
int sum = 0;
for (const auto& element : mst) {
if (findRoot(parentArr, element.second.first) != findRoot(parentArr, element.second.second)) {
unionOperation(parentArr, element.second.first, element.second.second);
sum += element.first;
}
}
cout << "MST의 value = " << sum << '\n';
}Section3:: 위상정렬 (Topology sort)
개념
방향 그래프에 대해 방향성을 거스르지 않으면서 정점들을 정렬하는 알고리즘
설명

알고리즘 수업을 듣기 위해서는 자료구조 수업과 객체지향 프로그래밍 수업을 이수해야 한다고 생각해보자.
그러면 자료구조와 객체지향은 항상 알고리즘의 앞에 와야 한다.
이러한 방향성을 유지하면서 정점들을 나열하는 알고리즘을 위상정렬이라고 한다.
예시
- 먼저 모든 간선을 탐방하면서 모든 정점에 대해
indegree를 계산한다. indegree값이 0인 점을 시작 정점으로queue에 넣고BFS를 수행한다.queue에서pop()되는 원소들을 외부 컨테이너에 순서대로 저장한다.BFS를 수행할 때, 간선에 연결되는 정점은indegree를 하나 감소시킨다. 이때 0이 된다면queue에push()한다.
코드
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int V, E, indegree[1001];
vector<int> graph[1001];
void topologySort() {
vector<int> answer;
queue<int> q;
for (int i = 1; i <= V; ++i)
if (indegree[i] == 0) q.push(i); // indegree가 0인 점을 시작점으로 push한다.
while(!q.empty()) {
int curVertex = q.front(); q.pop();
answer.push_back(curVertex);
for (const int& next : graph[curVertex]) {
indegree[next]--;
if (indegree[next] == 0) q.push(next);
}
}
for (const int& ele : answer)
cout << ele << ' ';
cout << '\n';
}
int main() {
ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
cin >> V >> E;
for (int i = 0; i < E; ++i) {
int s, e; cin >> s >> e;
graph[s].push_back(e);
indegree[e]++; // 종점에 대해 indegree를 하나 증가한다.
}
topologySort();
}