<모든 문제는 C++를 기반으로 풀이한다.>

Greedy 부분 문제 풀이 및 해설

1. 큰 수의 법칙

• 주어진 조건에서 가장 큰 수를 만드는 방법은 수열을 정렬하고, 가장 큰 수를 K번 더한 뒤 두번째로 큰 수를 한 번 더하는 과정을 반복하는 것이다.
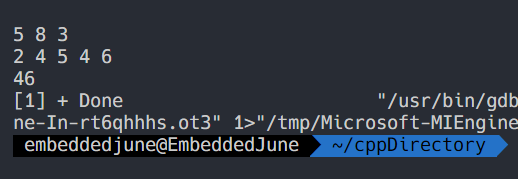
• 2 4 5 4 6을 예로들어보자. 정렬하면, 2 4 4 5 6이 되고, M = 8, K = 3일 때, 우리는 가장 큰 수 6을 3번 더하고 5를 1번 더하고 다시 6을 3번 더하고 5를 1번 더하면 된다. $6 + 6 + 6 + 5 + 6 + 6 + 6 + 5 = 46$
• 따라서 이 문제는 두 가지 방법으로 풀 수 있다.
  • 컴퓨터의 힘을 믿고 for문으로 가장 큰 요소를 한 번씩 더한다. K의 배수번째마다 두 번째로 큰 수를 더하고 이를 반복한다.
  • 결국 가장 큰 요소는 K번 곱해지고 두 번째로 큰 요소는 1번 더해지므로 수식으로 나타내면 $K \times (가장 \ 큰 \ 요소) + (두 \ 번째로 \ 큰 \ 요소)$ 이고 이러한 덩어리가 $M / (K + 1)$개 존재한다. 그리고 나머지 $M\ \% \ (K + 1)$개는 따로 처리해준다.
• 무엇을 선택하든 자유다. 두 번째 방법이 더 빠른건 당연하다.

#include <iostream>
#include <algorithm>
using namespace std;

int main() {
	ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
	int N = 0, M = 0, K = 0;	// 배열크기, 덧셈회수, 연속가능개수
	cin >> N >> M >> K;

	int arr[N];
	for (int i = 0; i < N; ++i) cin >> arr[i];
	sort(arr, arr + N);		// 정렬한다. 제일 큰 두 요소만 필요하다.

	int ans = ((M / (K + 1)) * (K * arr[N - 1] + arr[N - 2])) + (M % (K + 1)) * arr[N - 1];
	cout << ans << '\n';
}

2. 숫자 카드 게임

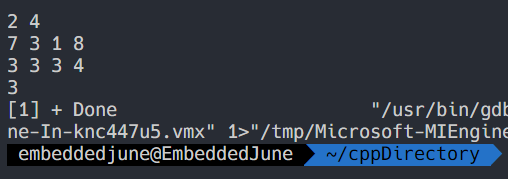
• 이 문제는 한 문장으로 요약하면, N개의 각 행에서 가장 작은 원소들 사이에서 가장 큰 원소의 값은 무엇인가? 이다.
• 따라서 행 단위로 입력을 받고, 해당 행의 최소 원소는 따로 취급해준다.
• 그리고 sort() 함수 또는 find_max 함수를 이용해주면 된다.

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main() {
	ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
	int row = 0, col = 0;	cin >> row >> col;
	vector<int> smallestArr;
	for (int y = 0; y < row; ++y) {
		int rowSmallestElem = INT16_MAX;
		for (int x = 0; x < col; ++x) {
			int elem = 0; cin >> elem;
			rowSmallestElem = min(rowSmallestElem, elem);
		}	// 각 행에서 가장 작은 원소를 찾은 뒤 배열에 넣는다.
		smallestArr.push_back(rowSmallestElem);
	}
	
	sort(begin(smallestArr), end(smallestArr));
	cout << smallestArr.back() << '\n';
}

3. 1이 될 때까지

• Greedy에 따라 1을 감산하는 것 보다 K로 나누는게 훨씬 빠르다라는 것을 떠올릴 수 있다. 그러므로 우리는 가능한 한 많이 K로 나눠야 한다.

#include <iostream>
using namespace std;

int main() {
	int N = 0, K = 0; cin >> N >> K;
	int ans = 0;
	while (N != 1) {			// 기저: N이 1이 될 때까지 반복한다.
	    if (N % K == 0) N /= K;		// 나누어 떨어지면 방법 2 사용
	    else N--;				// 아니면 방법 1 사용
	    ans++;
	}
	cout << ans << '\n';
}

• 쉬운 문제라 딱히 해설이 필요하진 않다.