<모든 코드는 C++를 기반으로 작성되었습니다.>

Chapter 9 :: 최단 경로

예제 1. 다익스트라 알고리즘 구현

• 다익스트라 알고리즘은 임의의 기준 정점으로부터 모든 정점까지의 최단 경로를 빠르게 찾는 방법이다.
• 다익스트라 알고리즘의 시간 복잡도는 간선 개수 E, 정점 개수 V일 때,
  $O(E \times log(V))$이다.
• 코딩 테스트를 준비하는 사람이라면, 다익스트라 알고리즘은 자다가 일어나서 구현할 수 있을 정도로 굉장히 숙달되어야 한다.
• 동빈나씨의 github에서 제공되는 원본 C++ 코드와 굉장히 비슷하지만 다른 구석이 있다면, min heap의 구현 과정이 조금 다른 점이다. priority_queue<p, vector<p>, greater<p>> pq로 구현한 점을 잘 알아두자.

// 다익스트라 알고리즘
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;

static int N, M, startVertex, dist[100001];
static vector<pair<int, int>> graph[100001];

void dijkstra() {
	priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
	pq.push({0, startVertex});
	dist[startVertex] = 0;
	
	while(!q.empty()) {
		int curVertex = q.front().second, curDist = q.front().first;
		q.pop();
		
		if (dist[curVertex] <= curDist) continue;
		
		for (int i = 0; i < graph[curVertex].size(); ++i) {
			int nextVertex = graph[curVertex][i].first;
			int nextDist = curDist + graph[curVertex][i].second;
			if (dist[nextVertex] > nextDist) {
				dist[nextVertex] = nextDist;
				pq.push({nextDist, nextVertex});
			} 
		}
	}
}

int main() {
	ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
	cin >> N >> M >> startVertex;
	for (int i = 0; i < M; ++i) {
		int sv, ev, weight;	cin >> sv >> ev >> weight;
		graph[sv].push_back({ev, weight});
	}
	fill(dist, dist + N, 1e9);
	dijkstra();
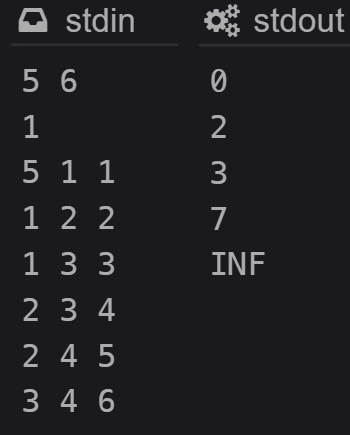
	for (int i = 1; i <= N; ++i)
		(dist[i] == 1e9) ? (cout << "INF\n") : (cout << dist[i] << '\n');
}

예제 2. 플로이드 알고리즘 구현

• 플로이드 알고리즘은 모든 기준 정점으로부터 모든 정점까지의 최단 경로를 빠르게 찾는 방법이다.
• 플로이드 알고리즘의 시간 복잡도는 $O(n^3)$이다.
• 코딩 테스트를 준비하는 사람이라면, 플로이드 알고리즘 또한 자다가 일어나서 구현할 수 있을 정도로 굉장히 숙달되어야 한다.

// 플로이드-워셜 알고리즘  
#include <iostream>
using namespace std;

static constexpr int MAX = 1e9;
static int N, M, graph[501][501];

int main() {
	ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
	cin >> N >> M;	// N: 노드개수, M: 간선개수
	for (int i = 0; i < 501; ++i) {
		fill(graph[i], graph[i] + 501, MAX);
		graph[i][i] = 0;
	}
	for (int i = 1; i <= M; ++i) {
		int s, f, w;	cin >> s >> f >> w;
        	// 굳이 갱신할 필요가 없는 경우, 갱신하지 않는다. 
		if (graph[s][f] != MAX && graph[s][f] < w) continue;
		graph[s][f] = w;
	}
	// 플로이드-워셜 알고리즘 O(n^3)
	for (int k = 1; k <= N; ++k)		 // k번째 노드에 대해 테이블 갱신
		for (int s = 1; s <= N; ++s)	 // 모든 출발 정점에 대해 반복
			for (int f = 1; f <= N; ++f) // 모든 도착 정점에 대해 반복
				graph[s][f] = min(graph[s][f], graph[s][k] + graph[k][f]);
	// 수행 결과를 출력
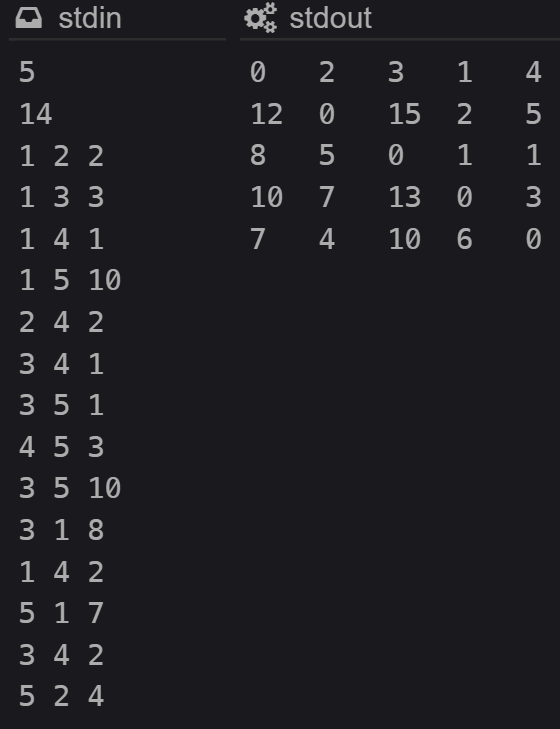
	for (int s = 1; s <= N; ++s) {
		for (int f = 1; f <= N; ++f) {
			if (graph[s][f] == MAX) cout << "INF" << ' ';
			else cout << graph[s][f] << ' ';
		}
		cout <<'\n';
	}
}

예제 3. 미래 도시

• 교재에서는 플루이드 알고리즘으로 풀이했지만, 다익스트라 알고리즘으로 풀 수 있다.
• 1번 도시부터 K번 도시까지 다익스트라 1번, K번 도시부터 X번 도시까지 다익스트라 1번을 사용하면, 플루이드 알고리즘을 사용한 풀이보다 빠르게 풀 수 있다.

// 미래도시
#include <iostream>
#include <vector>
#include <queue>
using namespace std;

int N, M, X, K, shortestPathList[101];
vector<int> graph[101];

int dijkstra(int startV, int targetV) {
	priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq; // Min Heap 구현
	pq.push({0, startV});
	fill(shortestPathList, shortestPathList + 101, 1e9);	// 최소 간선 길이 테이블 초기화.
	shortestPathList[startV] = 0;
	// 다익스트라 알고리즘
	while (!pq.empty()) {
		int dist = pq.top().first, curV = pq.top().second; pq.pop();
		
		if (shortestPathList[curV] < dist) continue;
		for (int i = 0; i < graph[curV].size(); ++i) {
			int newDist = dist + 1, nextV = graph[curV][i];
			if (shortestPathList[nextV] > newDist) {
				shortestPathList[nextV] = newDist;
				pq.push({newDist, nextV});
			}
		}
	}
	return shortestPathList[targetV];
}

int main() {
	ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
	cin >> N >> M;	// N: 회사개수, M: 도로개수
	for (int i = 1; i <= M; ++i) {
		int s, f; cin >> s >> f;
		graph[s].push_back(f);
		graph[f].push_back(s);
	}
	cin >> X >> K;	// X: 도착지점, K: 소개팅지점
	int ans = dijkstra(1, K) + dijkstra(K, X);
	if (ans >= 1e9) cout << -1 << '\n';
	else cout << ans << '\n';
}

예제 4. 전보

// 전보
#include <iostream>
#include <vector>
#include <queue>
using namespace std;

int N, M, C, shortestPathList[30001];
vector<pair<int, int>> graph[30001];

void dijkstra() {
	priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq; // Min Heap 구현
	pq.push({0, C});
	fill(shortestPathList, shortestPathList + 101, 1e9);	// 최소 간선 길이 테이블 초기화.
	shortestPathList[C] = 0;
	// 다익스트라 알고리즘
	while (!pq.empty()) {
		int dist = pq.top().first, curV = pq.top().second; pq.pop();
		
		if (shortestPathList[curV] < dist) continue;
		for (int i = 0; i < graph[curV].size(); ++i) {
			int newDist = dist + graph[curV][i].second, nextV = graph[curV][i].first;
			if (shortestPathList[nextV] > newDist) {
				shortestPathList[nextV] = newDist;
				pq.push({newDist, nextV});
			}
		}
	}
}

int main() {
	ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
	cin >> N >> M >> C;	// N: 도시개수, M: 통로개수, C: 응급도시
	for (int i = 1; i <= M; ++i) {
		int s, f, w; cin >> s >> f >> w;
		graph[s].push_back({f, w});
	}
	dijkstra();
	int cntCity = -1, cntTime = 0;
	for (int i = 1; i <= N; ++i)
		if (shortestPathList[i] != 1e9) {
			cntTime = max(cntTime, shortestPathList[i]);
			cntCity++;
		}
	cout << cntCity << ' ' << cntTime << '\n';
}

• 이 문제 역시 응급도시로부터의 최단거리를 구하면 되는 다익스트라 문제다.
• 답을 구할 때 응급도시 자신이 포함되므로 -1부터 시작했다.