프로그래밍 대회에서 배우는 알고리즘 문제해결 전략 책 내용 정리입니다.

30.1 도입

가중치가 없는 그래프의 최단 경로: BFS로 하면 됨

최단 경로 알고리즘

• 최단 경로의 길이를 찾아줌
• 실제 경로를 계산하려면 탐색 과정에서 별도의 정보를 저장해야 함

음수 간선의 중요성

가중치 합이 음수인 사이클이 있으면 최단 경로 문제가 정의되지 않음

→ 최단 경로 찾기 불가

단, 알고리즘에 따라 음수 가이클이 존재한다는것 확인 가능

단일 시작점과 모든 쌍 알고리즘

단일 시작점 알고리즘

• 하나의 시작점에서 다른 모든 정점까지 가는 최단 거리
• BFS와 비슷

모든 쌍 알고리즘

• 모든 정점의 쌍에 대해 최단 거리 계산
• 수행 결과: V*V 크기의 배열
• 예시: 플로이드 알고리즘

방향 그래프와 무방향 그래프

(이 절에서 다루는) 최단 거리 알고리즘들은 방향 그래프 기준으로 동작

무방향 그래프에서 최단 경로 찾기

→ 양방향 간선을 2개의 일방 통행 간선으로 쪼개서 방향 그래프로 만들어야 함

주의: 음수 가중치가 있으면, 음수 사이클이 생김

→ 최단 경로 문제 풀이 불가

30.2 다익스트라의 최단 경로 알고리즘

• 단일 시작점 최단 경로 알고리즘
• 시작 정점 s에서부터 다른 정점들까지의 최단 거리 계산

우선순위 큐를 사용하는 너비 우선 탐색

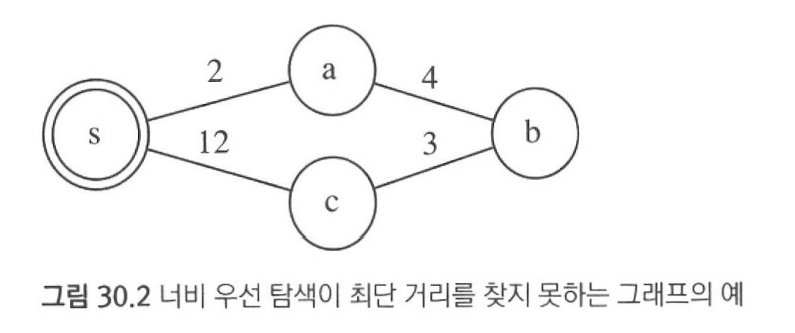
너비 우선 탐색: 정점을 발견한 순서대로 방문

s→a→c→b

최단거리: s→a→b→c

• 더 늦게 발견한 정점이라도 더 먼저 방문할 수 있어야 함

⇒ 우선순위 큐 사용

• 우선순위 큐
  • 정점의 번호, 지금까지 찾아낸 해당 정점까지의 최단 거리 쌍
  • 정점까지의 최단 거리를 기준으로 정점 배열

구현

1. 각 정점까지의 최단 거리를 저장하는 배열 dist[]를 유지하며, 정점을 방문할 때마자 인접한 정점 모두 검사
2. 간선 (u, v)를 검사했는데, v가 아직 방문하지 않은 정점이라면
   1. u까지의 최단거리에 (u, v)의 가중치를 더해 v까지의 경로의 길이를 찾음
3. 2의 결과가 지금까지 우리가 찾은 최단 거리라면
   1. dist[v]를 갱신하고, (dist[v], v)를 큐에 넣음

주의점

• 각 정점까지의 최단 경로가 갱신될 수 있음

• 우선순위 큐에 들어있는 이전 최단 경로에 대한 처리 필요

  방법

  1. 우선순위 큐 내에서 이전 값을 찾아 업데이트
  2. 이전 값을 그대로 두고, 새로운 값을 추가한뒤, 나중에 큐에서 이전 값이 꺼내지면 무시
  • 실제로 2번 방식을 주로 사용
  • 큐에서 정점 번호 u와 최단거리 cost의 쌍을 뽑아낸 후
  • dist[u]와 cost를 비교
    • dist[u] < cost라면, u까지 오는 cost보다 짧은 경로가 이미 발견됐다는 의미이므로 (cost, u) 쌍은 무시

시간복잡도

인접한 간접 검사: $O(E)$

우선순위 큐 삽입/삭제:

$O(|E|log|E|) < O(|E| * 2log|V|)$ 이므로 $O(|E|log|V|)$

결론: $O(|E|log|V|)$