ABSTRACT

그래프 신경망(GNN)은 그래프를 위한 표준 학습 아키텍처가 되었다. GNN은 양자 화학, 추천 시스템, 지식 그래프 및 자연어 처리에 이르기까지 다양한 영역에 적용되어 왔다. 임의 그래프의 주요 문제는 노드의 표준 위치 정보가 없다는 것인데, 이는 예를 들어 동형 노드 및 기타 그래프 대칭을 구별하기 위해 GNN의 표현력을 감소시킨다. 이 문제를 해결하기 위한 접근 방식은 노드의 위치 인코딩(PE)을 도입하고 트랜스포머에서와 같이 입력 계층에 주입하는 것이다. 가능한 그래프 PE는 라플라시안 고유 벡터입니다.본 연구에서는 네트워크가 이러한 두 가지 필수 속성을 쉽게 학습할 수 있도록 구조 및 위치 표현을 분리할 것을 제안한다. 우리는 LSP(Learnable Structural and Positional Encoding) 라고 하는 새로운 일반 아키텍처를 소개한다. 우리는 몇 가지 희소하고 완전히 연결된 (트랜스포머와 같은)을 조사한다. GNN은 두 GNN 클래스에 대해 학습 가능한 PE를 고려할 때 분자 데이터 세트의 성능 향상을 1.79%에서 최대 64.14%로 관찰한다.

1 INTRODUCTION

GNN은 최근 복잡한 데이터 연결을 인코딩하는 이질적인 그래프 형태로 정보가 존재하는 데이터 세트를 분석하는 강력한 딥 러닝 아키텍처 클래스로 부상했다. 실험적으로, 이러한 아키텍처는 약물 설계(Stokes et al., 2020; Gaudlet et al., 2020), 소셜 네트워크(Monti et al., 2019; Pal et al., 2020), 교통 네트워크(Derrow-Pinion et al., 2021), 물리학(Cranmer et al., 2019; Bapst et al., 2020), 최적기(Combiation)와 같은 다양한 영역에서 큰 가능성을 보여주었다. 2021년, 카파트 외, 2021년) 및 의료 진단(Li 외, 2020c).

대부분의 GNN(예: Deferrard et al. (2016) Sukhbatar et al. (2016); Kipf & Welling (2017);해밀턴 외(2017); 몬티 외(2017); 브레송 & 로랑(2017); 벨리코비 외(2018); 쉬 외(2019)는 지역 이웃 정보를 집계하여 노드 표현을 구축하는 메시지 전달 메커니즘으로 설계되었다(길머 외, 2017). 이는 GNN의 이 클래스가 근본적으로 구조적이라는 것을 의미한다. 즉, 노드 표현은 그래프의 로컬 구조에만 의존한다는 것이다. 이와 같이, 같은 이웃을 가진 분자 내의 두 원자는 유사한 표현을 가질 것으로 예상된다. 그러나, 분자 내에서의 두 원자의 위치가 구별되기 때문에 이 두 원자에 대해 동일한 표현을 갖는 것은 제한적일 수 있으며, 이들의 역할은 구체적으로 분리될 수 있다(Murphy et al., 2019). 결과적으로, 인기 있는 메시지 전달 GNN(MP-GNN)은 동일한 1홉 로컬 구조를 가진 두 노드를 구별하지 못한다. 이 제한은 이제 그래프 동형을 위한 Weisfeiler-Leman(WL) 테스트(Weisfeiler & Leman, 1968)와 MP-GNN의 동등성의 맥락에서 적절하게 이해된다(Xu 등, 2019; Morris 등, 2019).

상기 제한은 (i) 여러 레이어를 적층하거나 (ii) 고차 GNN을 적용하거나 (iii) 노드(및 에지)의 위치 인코딩(PE)을 고려함으로써 어느 정도 완화될 수 있다. 1홉 이웃은 같지만 2홉 이상 이웃과 관련하여 다른 두 개의 구조적으로 동일한 노드를 그래프에서 가정합시다. 그런 다음 여러 레이어(Bresson & Laurent, 2017; Li et al., 2019)를 쌓으면 노드에서 여러 홉으로 정보를 전파할 수 있으므로 두 개의 먼 노드의 표현을 구별할 수 있다. 그러나 이 솔루션은 과도한 스쿼싱 현상으로 인해 장거리 노드에 부족할 수 있다(Alon & Yahav, 2020). 다른 접근법은 WL 기반 GNN(Maron et al., 2019; Chen et al., 2019)과 같은 고차 노드 튜플 집계를 계산하는 것이다. 이러한 모델은 중간 크기의 그래프에서도 MP-GNN보다 스케일링 비용이 더 많이 든다(Dividei et al., 2020). 대안 기법은 노드 간 그래프 기반 거리를 인코딩하거나(You et al., 2019; Dwivedi et al., 2020; Li et al., 2020b; Dwivedi & Bresson, 2021), 특정 하위 구조에 대해 알릴 수 있는 그래프의 노드의 전역 위치를 고려하는 것이다(Bouritas et al., 2020; Bodnar et al., 2021).

Contribution

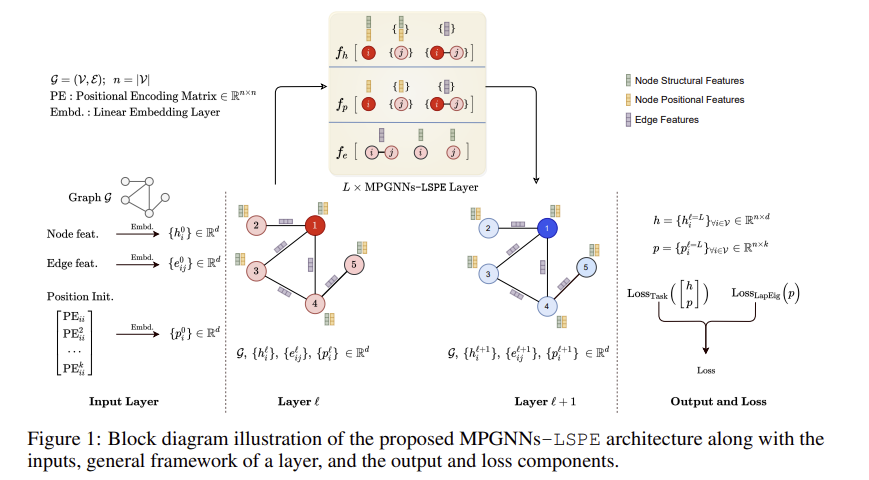
본 연구에서는 구조적 GNN과 결합하여 보다 표현력 있는 노드 임베딩을 생성할 수 있는 위치 표현을 학습하는 아이디어로 눈을 돌린다. 우리의 주요 의도는 임의 그래프에서 노드의 표준 위치 부족을 완화하여 MP-GNN의 표현력을 향상시키는 동시에 대규모 애플리케이션의 선형 복잡성을 유지하는 것이다. 이 목적을 위해, 우리는 그림 1과 함께 GNN이 구조적 표현과 위치 표현을 동시에 학습할 수 있도록 하는 새로운 프레임워크를 제안한다(따라서 MPGNNs-LSPE라고 명명됨). 이와 함께 노드의 위치 표현을 초기화하기 위해 랜덤 워크 확산 기반 위치 인코딩 체계를 제시한다. 우리는 학습 가능한 PE가 있는 제안된 아키텍처를 MP-GNN 프레임워크에 맞는 모든 그래프 네트워크와 함께 사용할 수 있으며 성능을 향상시킨다는 것을 보여준다(1.79%~64.14%). 우리의 시연에서, 우리는 Gated와 같은 두 희소 GNN의 LSP 인스턴스를 공식화한다.GCN(Bresson & Laurent, 2017)과 PNA(Corso et al., 2020) 및 완전히 연결된 트랜스포머 기반 GNN(Kreuzer et al., 2021; Mialon et al., 2021). 세 가지 표준 분자 벤치마크에 대한 우리의 수치 실험은 LSPE를 사용한 MP-GNN의 서로 다른 인스턴스화가 한 데이터 세트에서 이전의 최첨단(SOTA)을 상당한 차이(26.23%) 능가하는 동시에 다른 두 데이터 세트에서 SOTA 비교 가능한 점수를 달성한다는 것을 보여준다. 이 아키텍처는 또한 세 가지 비분자 벤치마크에서 일관된 개선을 보여준다. 또한, 우리의 평가는 희소 MP-GNN이 완전히 연결된 GNN보다 성능이 우수하다는 것을 발견하여, 그래프를 위한 매우 효율적이지만 강력한 아키텍처의 개발에 대한 더 큰 잠재력을 시사한다.

2 RELATED WORK

You et al. (2019)은 무작위 앵커 노드 세트를 기반으로 학습 가능한 위치 인식 임베딩을 제안했는데, 여기서 앵커의 무작위 선택은 한계를 가지고 있어 귀납적 작업에 대한 접근 방식을 덜 일반화한다. 또한 MP-GNN을 더 표현력 있게 만드는 분자에 대한 링(Bouritas et al., 2020; Bodnar et al., 2021)과 같은 관심 그래프 클래스에 대한 사전 정보를 인코딩하는 방법이 있다. 그러나 그래프 하위 구조에 대한 사전 정보는 사전 계산이 필요하며, 하위 그래프 매칭 및 카운팅은 k-tuple 하위 구조에 대한 O(nk)가 필요하다.

3 PROPOSED ARCHITECTURE

이 작업에서, 우리는 네트워크가 이러한 두 가지 중요한 특성을 쉽게 학습할 수 있도록 구조 및 위치 표현을 분리한다. 이는 대부분의 기존 아키텍처와 대조적이다.Dwivedi & Bresson (2021년); Beani 등(2021년), 위치 정보를 GNN의 입력 계층에 주입하는 Kreuzer 등(2021년)과 일반적인 유도 사용을 제한하는 노드의 거리 측정 앵커 세트에 의존하는 You 등(2019년)이다. 표현형 GNN에 대한 정보 그래프 PE의 중요성에 대한 최근 이론적 결과(Murphy et al., 2019; Srinivasan & Ribeiro, 2019; Loukas, 2020)를 고려할 때, 우리는 GNN이 표현력을 높이기 위해 위치 및 구조적 표현을 분리할 수 있는 일반적인 프레임워크에 관심이 있다. 섹션 3.1은 학습 가능한 그래프 PE로 GNN을 보강하는 우리의 접근 방식을 소개한다. 우리의 프레임워크는 다른 GNN 아키텍처와 함께 사용될 수 있다. 우리는 구조 및 위치 정보의 디커플링이 희소 MP-GNN과 완전히 연결된 GNN 모두에 적용되는 섹션 C.1과 C.2에서 이러한 유연성을 설명한다.

3.1 GENERIC FORMULATION: MP-GNNS-LSPE

표준 MP-GNN과 이 아키텍처(분리)의 차이점은 이러한 학습 가능한 PE와 노드 구조 특징인 Eq(7)의 연결과 함께 위치 표현 업데이트 Eq(9)를 추가하는 것이다. 다음 절에서 보게 될 것처럼, 메시지 전달 함수 fp의 설계는 fh와 동일한 분석 형식을 따르지만 위치 좌표에 양의 값과 음의 값을 허용하기 위해 tanh 활성화 함수를 사용합니다. 몇몇 MP-GNN은 h 업데이트에 에지 기능을 포함하지 않기 때문에 에지 기능인 e'ij를 h 업데이트에 포함시키는 것은 선택 사항이라는 점에 유의해야 한다. 그럼에도 불구하고, 우리가 제시하는 아키텍처는 편리한 방식으로 향후 확장에 사용될 수 있도록 일반화되어 있다.

Definition of initial PE.

Li et al.(2020b)에서 영감을 받아, 우리는 무작위 보행(RW) 확산 과정을 기반으로 한 PE인 RWPE를 제안한다(다른 그래프 확산은 s.a.로 간주될 수 있지만). 페이지랭크 (Mialon et al., 2021) 공식적으로 RWPE는 무작위 보행의 k 단계를 사용하여 다음과 같이 정의된다.

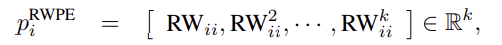
여기서 RW = AD-1은 랜덤 워크 연산자입니다. 모든 쌍방향 노드에 대해 전체 행렬 RWij를 사용하는 Li 등(2020b)과 대조적으로, 우리는 노드 i 자체의 착지 확률, 즉 RWii만을 고려하여 무작위 보행 행렬의 저복잡도 사용을 채택한다. 이러한 PE는 LapPE의 부호 모호성을 겪지 않으므로 네트워크가 추가 불변성을 학습할 필요가 없다는 점에 유의하십시오. RWPE는 각 노드가 충분히 큰 k에 대해 고유한 k-홉 위상 인접을 갖는 조건에서 고유한 노드 표현을 제공한다. 이 가정은 논의될 수 있다. CSL 그래프(Murphy et al., 2019)와 같은 합성 강정규 그래프를 고려한다면, 그래프의 모든 노드는 구성에 의해 동형이기 때문에 모든 k 값에 대해 동일한 RWPE를 갖는다. 그러나 RWPE가 그래프의 모든 노드에서 동일함에도 불구하고, 이러한 PE는 동형 그래프의 각 클래스에 대해 고유하므로 CSL 데이터 세트의 완벽한 분류가 가능하다(섹션 A.1 참조). Decalin 및 Bicyclopentyl (Sato, 2020)과 같은 그래프의 경우, 동형이 아닌 노드는 섹션 A.1에서도 § 5의 다른 RWPE 포크를 받는다. 마지막으로, ZINK 분자와 같은 실제 그래프의 경우, 대부분의 노드는 k ≥ 24에 대한 고유한 노드 표현을 받는다. 그림 2를 참조하라. 두 분자는 각각 100%와 71.43%의 고유한 RWPE를 갖는다. 섹션 A.3은 상세한 연구를 제시한다.
실험적으로, 우리는 RWPE가 LapPE보다 성능이 뛰어나다는 것을 보여주며, 각 노드에 대해 고유한 노드 표현을 정확히 가지지 않는 것보다 부호 불변성을 학습하는 것이 (각 그래프에 대해 2k개의 가능한 부호 플립이 존재하기 때문에) 더 어렵다는 것을 제안한다. CSL에 대해 위에서 언급한 바와 같이, RWPE는 그래프 동형성과 고차 노드 상호 작용의 문제와 관련이 있다. 정확하게 적절한 수의 단계에 대해 무작위 보행 연산자를 반복하면 비동형 노드에 색을 칠할 수 있으므로 1-WL 테스트 및 동등한 MP-GNN이 실패한 비동형 그래프의 여러 경우를 구별할 수 있다. CSL, 데칼린 및 Bicclopentyl 그래프. 반복 알고리즘의 공식 발표는 섹션 A.2를 참조한다. 마지막으로 네트워크의 초기 PE는 LapPE 또는 RWPE를 d차원 형상 벡터에 내장하여 얻는다.

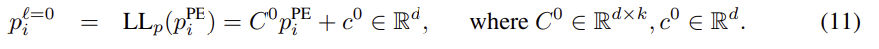
Positional loss.

구조적 표현과 위치 표현의 학습을 분리함에 따라 작업 손실과 함께 특정 위치 인코딩 손실을 고려할 수 있다. 자연 후보는 그래프 위상에 의해 제한된 좌표계를 형성하도록 PE를 강제하는 라플라시안 고유 벡터 손실(Belkin & Niyogi, 2003; Lai & Osher, 2014)이다. 따라서 MP-GNNs-LSPE의 최종 손실 함수는 다음과 같은 두 가지 항으로 구성된다.

5 CONCLUSION

이 연구는 그래프 신경망에서 구조 및 위치 표현을 별도로 학습하는 새로운 접근 방식을 제시한다. 그 결과 아키텍처인 LSP는 GNN 표현을 훨씬 더 표현적으로 만드는 이 두 가지 핵심 특성에 대한 원칙적이고 효과적인 학습을 가능하게 한다. LSPE의 주요 설계 구성 요소는 i) PE 초기화, ii) 모든 GNN 계층에서 위치 표현을 분리, iii) 학습 과제를 위한 하이브리드 기능을 생성하기 위한 구조 및 위치 기능의 융합이다. 평가에 사용되는 벤치마크 데이터 세트에서 모델의 여러 인스턴스에서 일관된 성능 증가를 관찰한다. 우리의 아키텍처는 두 개의 희소 GNN과 두 개의 완전히 연결된 Transformer 기반에 의해 입증되었듯이 모든 희소 GNN 또는 Transformer GNN과 함께 사용될 수 있는 간단하고 보편적이다.우리의 수치 실험에서 GNN. 최근 문헌에서 볼 수 있듯이 GNN을 이론적으로 개선하기 위해 표현적 위치 인코딩을 통합하는 것의 중요성을 고려할 때, 우리는 이 논문이 GNN과 트랜스포머 모두에 대해 그래프 위치 인코딩을 개선하는 미래 모델을 개발할 때 고려할 수 있는 유용한 아키텍처 프레임워크를 제공한다고 믿는다.