Abstract
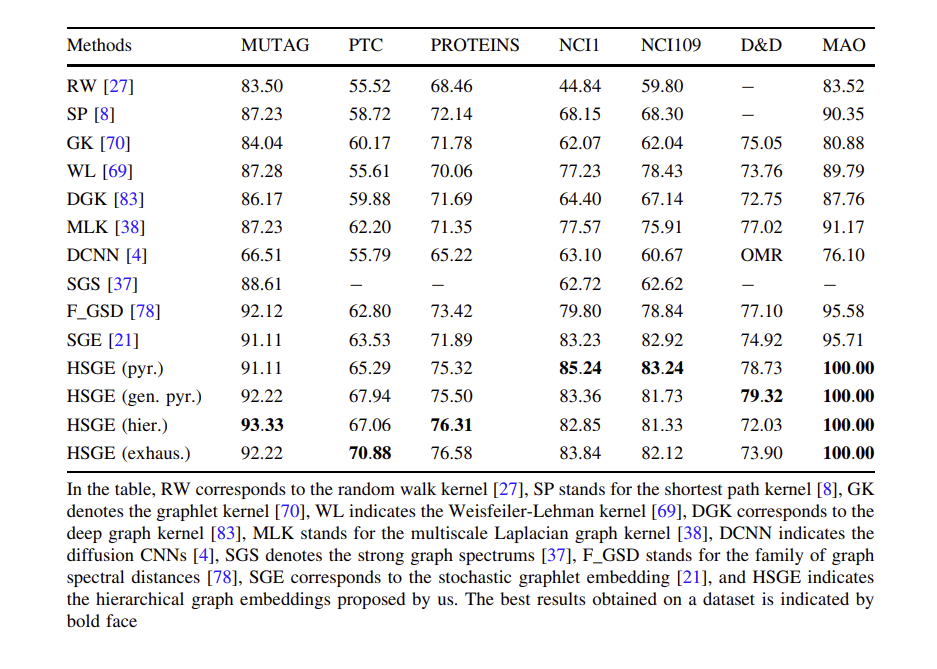
패턴 인식 및 기계 학습 커뮤니티 내에서 매우 성공했음에도 불구하고 그래프 도메인에 정의된 수학적 연산이 부족하기 때문에 그래프 기반 방법을 사용할 수 없는 경우가 많다. 그래프를 벡터 공간에 매핑하는 그래프 임베딩은 표준 기계 학습 기술을 사용할 수 있는 이러한 어려움을 해결하는 방법으로 제안되었다. 그러나 그래프 임베딩 기능은 일반적으로 구조 정보의 손실로 어려움을 겪는다는 것은 잘 알려져 있다. 본 논문에서는 이러한 정보 손실을 완화하는 방법으로 그래프의 계층 구조를 고려한다. 계층 구조는 그래프 노드를 위상적으로 클러스터링하고 각 클러스터를 상위 계층 수준의 노드로 간주하여 구성된다. 이 계층 구조가 구성되면 고전적인 그래프 임베딩이 주어지면 벡터 공간으로 매핑을 정의하기 위한 몇 가지 구성을 고려하며, 특히 확률적 그래프 임베딩(SGE)을 사용할 것을 제안 한다. 넓게 말하면, SGE는 벡터 공간에 그래프를 내장하는 방법으로 균일하게 샘플링된 저차에서 고차 그래프렛의 분포를 생성한다. 이후 그래프 계층의 거칠고 미세한 구조와 SGE가 가져온 통계는 서로를 보완하고 다양한 맥락의 중요한 구조 정보를 포함한다. 전체적으로, 이 두 가지 기술은 그래프 임베딩 기술과 관련된 일반적인 정보 손실을 실질적으로 처리하여 더 강력한 그래프 표현을 얻는다. 이러한 사실은 다양한 벤치마크 그래프 데이터 세트에 대한 상세한 실험 평가를 통해 입증되었으며, 여기서 우리는 최첨단 방법을 능가한다.
1 Introduction
그래프 기반 방법은 패턴 인식, 컴퓨터 비전 및 기계 학습 작업에 매우 성공적이었다[16, 25, 77]. 그러나 그래프에는 상징적, 관계적 특성으로 인해 전통적인 통계(벡터 기반) 표현과 비교하면 몇 가지 제한이 있다. 일부 사소한 수학적 연산은 그래프 영역에서 동등하지 않다. 예를 들어, 쌍별 합 또는 곱(많은 분류 및 클러스터링 알고리즘에서 기본 연산)은 그래프 영역에서 표준 방식으로 정의되지 않는다. 문헌에서, 이 문제가 해결된 가능한 방법은 함수를 내장하는 것이다. 그래프 공간 G가 주어졌을 때, 명시적 임베딩 함수는 주어진 그래프를 벡터 표현 [12, 29, 47, 65, 68]에 매핑하는 u: G-> R으로 정의되는 반면, 암시적 임베딩 함수는 주어진 그래프를 고차원 힐베르트 공간 H에 매핑하는 u: G->H로 정의되며, 여기서 점 곱은 두 그래프 KdG; G0 two 사이의 유사성을 정의한다.
그래프 영역에서 그래프를 암시적으로 내장하는 프로세스는 기본적으로 두 그래프 사이의 유사성을 계산하는 방법을 정의하는 그래프 커널로 불린다. 그러나 시간 효율성에 대한 제약과 기본 구조 정보를 보존할 때 이러한 임베딩 기능을 만드는 것은 매우 어렵다. 구조적 복잡성으로 인해 노이즈와 구조의 왜곡 가능성이 증가하고 정보가 손실될 위험이 높아지기 때문에 그래프의 크기가 커질수록 문제는 더욱 어려워진다. 계층적 표현은 종종 소음과 왜곡을 처리하는 방법으로 사용되며 [50, 76] 기본 객체에 대한 안정적인 묘사를 제공한다. 계층적 표현을 사용하면 공간 척도 표현에서 그래프를 점진적으로 축소할 수 있으므로 두드러진 특징(관련 하위 그래프)은 계층에 남아 있다. 따라서 최상위 수준은 작고 안정적인 요약이 된다.
다중 스케일 표현을 사용하여 정보를 처리하는 것은 컴퓨터 비전 및 이미지 처리 알고리듬에 성공적으로 사용되고 있으며, 이는 대부분 인간의 시각적 인식과 유사함[1]에서 영감을 얻었다. 자연주의적 시각적 해석은 항상 요약된 전역 사실뿐만 아니라 분산된 지역 정보를 나타낼 수 있는 데이터 구조를 필요로 한다는 것이 관찰된다[33]. 계층적 표현은 종종 로컬 기능에서 글로벌 정보를 효율적으로 추출하는 패러다임으로 사용된다. 그것 외에도, 계층적 모델은 시간 및 공간 효율적인 솔루션을 제공하는 것으로 여겨진다[76]. 위에서 언급한 직관과 관련 분야의 기존 연구에 동기를 부여받은 많은 저자들은 다양한 문제를 해결하기 위해 서로 다른 계층적 그래프 구조를 고안했다[22, 23, 48, 76]. 그런 의미에서 무사비 등의 작품을 언급할 가치가 있다. 그래프 임베딩을 위한 계층적 프레임워크를 제시한 [50]은 계층의 복잡한 인코딩을 탐구하지 않았다.
이 논문에서는 계층적 모델의 성공과 그래프 임베딩 이론의 효율성에 자극을 받아 먼저 주어진 그래프에서 계층적 구조를 생성한 다음 다중 스케일 구조를 활용하여 실제 벡터 공간에 그래프를 명시적으로 임베딩하는 일반적인 계층적 그래프 임베딩 공식을 제안한다. 먼저 [31]에서 제안된 그래프 클러스터링 알고리듬을 사용하여 주어진 입력 그래프의 계층적 그래프 표현을 얻는다. 여기서, 수준 i의 각 노드 클러스터는 상위 계층적 수준 i , 1의 단일 노드로 묘사되는 반면, 수준 내 에지는 기본 그래프의 원래 토폴로지에 따라 연결되며, 계층적 에지는 클러스터를 나타내는 노드를 하위 계층의 모든 노드에 결합함으로써 생성된다. 따라서, 우리는 우리의 계층 구조가 다른 그래프 추상화를 포함할 뿐만 아니라 계층적 에지를 통해 유용한 계층적 축소를 인코딩하기 때문에 무사비[50]보다 더 풍부한 인코딩을 제안한다.
그래프의 계층 구조가 생성되면 이 계층 정보를 활용하기 위해 확률적 그래프 임베딩(SGE) [21]의 새로운 사용을 제안한다. 한편, 우리는 SGE 설계 덕분에 지역 구성을 그래플릿의 형태로 활용할 수 있다. 왜냐하면 그래플릿은 서로 다른 이웃 크기의 정보를 제공하기 때문이다. 반면에, 계층적 연결은 더 추상적 정보를 인코딩하여 데이터에 존재하는 노이즈를 처리할 수 있게 한다. 결과적으로, 계층적 확률적 그래프 임베딩(HSGE)은 벡터 공간에 내장된 그래프의 전역적이고 컴팩트한 표현을 인코딩한다. 기본 그래프만 아닌 임베딩에 대한 전체 그래프 계층을 고려함으로써 표현 능력이 강화되고 그래프 임베딩 방법에서 일반적으로 발생하는 정보 손실을 처리한다. 또한 크기가 증가하는 균일하게 샘플링된 그래플릿에서 얻은 통계는 그래프 노드로 표현되는 서로 다른 객체 부분 간의 복잡한 상호 작용을 모델링한다. 여기서 계층적 그래프 구조와 크기가 증가하는 그래프렛의 통계는 다양한 컨텍스트의 중요한 구조 정보를 가져온다.
결과적으로, 우리의 접근 방식은 위에서 언급한 두 가지 전략의 이점을 얻을 수 있는 강력한 표현을 생성한다. 우리는 먼저 기호 관계 표현을 n차원 공간에 매핑하기 위한 임베딩 능력을 활용해서 기계 학습 접근 방식을 사용할 수 있다. 둘째, 계층 구조의 능력실제 데이터의 그래프 표현에 본질적으로 수반되는 노이즈와 왜곡을 줄여 보다 안정적이고 관련성이 높은 하부 구조를 간결하게 유지한다. 결론적으로, 우리 작업의 주요 기여는 그래프 임베딩 목적을 위해 기본 그래프만 연구하는 것이 아니라 주어진 그래프의 계층 구조를 활용하는 것이다. 그래프 피라미드의 계층적 정보를 평가하면 임베디드 그래프의 표현력을 확장하고 노이즈와 왜곡으로 인한 불안정성을 견딜 수 있다. 우리의 제안은 한편으로는 계층적 추상화의 구조적 정보를 구성하고 다른 한편으로는 무한 크기의 균일하게 샘플링된 그래플렛의 도움을 받아 객체 부분과 복잡한 상호 작용 사이의 관계를 고려하기 때문에 강력하다. 또한 제안된 방법은 일반적이며 프레임워크에서 다른 그래프 임베딩 알고리듬을 적용할 수 있다. 이러한 의미에서, 우리는 서로 다른 애플리케이션 도메인에서 오는 다양한 벤치마크 그래프 데이터 세트에서 제안된 알고리듬을 광범위하게 검증했다.
2 Related work
이어서, 우리는 본 논문의 주요 초점과 관련이 있다고 믿었던 명시적 및 암시적 그래프 임베딩 기술, 서로 다른 계층적 모델 및 그래프 요약 방법에 대한 관련 작업을 각각 검토한다.
2.1 Graph embedding
그래프 임베딩 방법은 주로 (1) 명시적 그래프 임베딩, (2) 암시적 그래프 임베딩 또는 그래프 커널의 두 가지 범주로 나뉜다.
2.1.1 Explicit graph embedding
명시적 그래프 임베딩은 그래프를 벡터 공간에 명시적으로 매핑하는 것을 목표로 하는 기술을 말한다. 이 범주에 속하는 방법들은 더 나아가 4개의 다른 등급으로 나눌 수 있다. 그래프 탐색 [47]으로 알려진 첫 번째 방법은 특정 하위 구조(내용 및 토폴로지를 캡처하는)의 빈도를 그래프로 측정해야 한다. 고려된 서로 다른 그래프 하위 구조(예: 노드, 에지, 하위 그래프 등)를 기반으로 서로 다른 임베딩 기술이 제안되었다. 예를 들어, Shervashidze 등이 있습니다. [68] 기버트 등은 비동형 그래플릿을 연구했지만 노드 레이블과 에지 관계 통계가 고려된다. [29][65]에서 Sound는 사전 처리된 행정 문서에서 하위 그래프 특징을 효율적으로 추출하기 위해 상향 그래프 격자를 도입했으며, Dutta와 Sahbi[21]는 벡터 공간에 그래프를 내장하기 위한 확률적 그래프렛 분포를 제안했다. 그래프 임베딩 기법의 두 번째 클래스는 스펙트럼 그래프 이론 [13, 34, 37, 39, 64, 82]을 기반으로 하며, 그래프의 고유 벡터/고윳값 또는 그래프의 라플라시안 행렬의 관점에서 그래프의 구조적 특성을 분석하는 것을 목표로 한다. 최근 Verma와 Zhang[78]은 강력한 그래프 특징 표현을 위해 그래프 스펙트럼 거리 패밀리를 제안했다. 그들의 상대적 성공에도 불구하고, 스펙트럼 방법은 구조적 노이즈와 왜곡에 상당히 취약하다. 세 번째 등급의 방법은 [56]에서 제안된 이종성 측정에서 영감을 받았다. 이러한 맥락에서, Bunke와 Riesen은 미리 선택된 다수의 프로토타입 그래프와의 거리에 따른 주어진 그래프의 벡터 설명에 대한 몇 가지 작업을 제시했다. [9, 12, 62, 63] 최근 딥 러닝과 신경망의 발전에 자극을 받아, 많은 연구자들은 그래프 [4, 17, 30, 36, 55]의 벡터 표현을 얻기 위해 신경망을 활용할 것을 제안했는데, 이는 기하학 딥 러닝이라는 네 번째 범주의 방법을 초래한다.
2.1.2 Implicit graph embedding
암시적 그래프 임베딩 또는 그래프 커널 방법은 주로 벡터 공간에 그래프를 임베딩하는 또 다른 방법이다. 또한 기존 기계 학습 알고리듬을 그래프, 문자열 등과 같은 비선형 데이터로 효율적으로 확장할 수 있는 능력으로도 인기가 있다. 그래프 커널 방법은 크게 세 가지 범주로 나눌 수 있다. 확산 커널로 알려진 첫 번째 것은 두 그래프의 하위 부분 간의 유사성 측정을 기반으로 하며, 두 그래프에 대한 전역 유사성 측정을 얻기 위해 전체 구조에 이를 전파한다[43, 72]. 컨볼루션 커널이라고 하는 두 번째 클래스의 방법은 부분(즉, 노드)의 유사성으로부터 복합 객체(그래프로 모델링)의 유사성을 측정하는 것을 목표로 한다[80]. 이러한 유형의 그래프 커널은 G와 G0의 하위 부분의 유사성 곱의 전체 분해 합으로부터 두 그래프 G, G0 사이의 유사성을 도출한다[52]. 최근, 콘도르와 Pan[38]은 두 그래프의 정점에 정의된 기본 커널을 그래프 사이의 커널로 리프팅하는 속성을 가진 다중 스케일 라플라시안 그래프 커널을 제안했다. 세 번째 클래스의 방법은 두 그래프 모두에 속하는 공통 하위 구조의 분석을 기반으로 하며 하위 구조 커널이라고 한다. 이 제품군에는 랜덤 워크 [27, 79], 백트랙리스 워크 [5], 최단 경로 [8], 하위 트리 [68], 그래프렛 [70]을 하위 구조로 고려하는 그래프 커널 방법이 포함된다. 위의 세 가지 범주와는 다른, 셰르바시제 외. [69] 원본 그래프를 일련의 그래프에 매핑하는 그래프 동형성의 Weisfeiler-Lehman 테스트에서 효율적인 그래프 커널 패밀리를 제안했다. 최근, 딥 러닝의 성공에 영감을 받아, 야나르다그와 비스와나단[83]은 그래프에 대한 하위 구조의 잠재적 표현을 학습하기 위한 통일된 프레임워크를 제시했다. 그들은 사전 계산된 그래프 커널이 주어지면 제안된 기법이 하위 구조의 숨겨진 표현을 활용하는 개선된 표현을 생성한다고 주장했다.
2.2 Hierarchical graph representation
일반적으로, 계층적 모델은 이미지 분할 [22, 48], 장면 분류 [23], 동작 인식 [54], 형상 분류 [18], 그래픽 인식 [10], 3D 객체 인식 [76] 등과 같은 컴퓨터 비전 및 이미지 처리 분야의 많은 다양한 영역에서 성공적으로 사용되었다. 이러한 접근 방식은 일반적으로 다양한 해상도의 정보를 포함하는 일종의 피라미드 구조를 이용한다. 일반적으로 피라미드의 가장 높은 수준에서 캡처된 정보는 로컬 기능과 관련된 반면, 더 거친 수준에서 기본 데이터의 전역적 측면이 표현된다. 이러한 표현 방식은 지식을 자연주의적으로 해석하는 데 도움이 된다[33]. 위의 직관에 영감을 받아, 그래프 표현에서 거칠고 미세한 정보를 추출하기 위해 계층 구조가 종종 사용된다. 펠릴로 외 [57]은 동적 프로그래밍 접근법으로 해결된 연관 그래프에서 두 계층 구조를 패거리 감지 문제로 일치시킬 것을 제안했다. [71]에서 쇼쿠판데 등은 방향성 비순환 그래프의 위상 정보를 포함하는 계층 구조를 인덱싱하기 위한 스펙트럼 특성화 기반 프레임워크를 제시했다. 물체의 계층적 표현과 탄성 매칭 절차도 [24]에서 변형 가능한 형상 매칭으로부터 제안된다. [46]에서 류 외 연구진. 계층적 그래프 표현과 계층적 형상 일치 및 등록 문제를 위한 확률적 샘플링 전략을 활용했다. 각 경로가 연속적인 단순화를 인코딩하는 계층과 연관된 계층적 경로 백을 기반으로 하는 그래프 커널이 [18]에 제시되어 있다. Ahuja와 Todorovic [2]은 객체 인식을 위해 분할 영역의 계층적 그래프를 사용했다. 그들에게 동기부여를 받은 브로엘만 외 연구진. [10, 11]은 그래픽 기호의 오류 허용 일치에 대한 계층적 그래프를 기반으로 밀접하게 관련된 두 가지 접근법을 제안했다. 무사비 외. [50] 그래프 피라미드의 다른 수준을 고려하는 계층적 그래프 표현에 기반한 그래프 임베딩 전략을 제안했다. 그들은 제안된 프레임워크가 모든 종류의 그래프 임베딩 기술을 통합할 수 있을 만큼 충분히 일반적이라고 주장했다. 그러나 저자들은 복잡하고 풍부한 계층 인코딩을 이용하지 않았다. 문헌 검토를 통해, 우리는 계층적 그래프 구조를 이용하는 그래프 영역에 일부 작품이 있지만, 대부분은 일종의 오류 허용성 또는 탄력적 매칭에 초점을 맞추고 있다는 결론을 내릴 수 있다. 벡터 공간 임베딩을 위한 그래프의 이러한 유형의 다중 스케일 표현 활용은 매우 드물고 아직 제대로 탐구되지 않았다. 이 사실은 명시적인 그래프 임베딩 작업을 위한 그래프 계층 구조에서 작업하려는 우리의 동기로 작용했다.
3 Definitions and notations
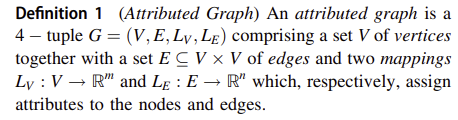


4 Hierarchical embedding
문헌에서, 오직 소수의 임베딩 접근법만이 다중 규모 또는 추상화 정보의 개념을 이용한다[38]. 이 섹션은 그래프 임베딩이 주어지면 이 정보를 포함할 수 있는 프레임워크를 제공하기 위해 전념한다. 문헌[20, 50, 59]에서 언급된 다중 스케일 정보를 활용하기 위해 제안된 일부 연구는 계층적 에지가 제공하는 계층적 정보를 폐기하고 원본 그래프의 추상화에 초점을 맞춘다.
4.1 Graph clustering
그래프 클러스터링은 사회 및 생물학적 네트워크[31], 추천 시스템[28, 44] 등과 같은 여러 분야에서 널리 사용되어 왔다. 대략 그래프 구조에 따라 그래프 노드를 클러스터로 그룹화하는 작업으로 설명할 수 있다. 이상적으로, 그룹화는 클러스터 내 노드가 조밀하게 연결된 반면 클러스터 간 노드 간의 연결은 희박하게 이루어지는 방식으로 수행되어야 한다. 예를 들어, Girvan과 Newman[31]은 사회 및 생물학적 네트워크를 연구하기 위한 커뮤니티 구조를 탐지하기 위한 그래프 클러스터링 알고리즘을 제안한다. Li 외. [28, 40, 44, 45]는 컨텍스트 인식 [28], 주파수 속성 포함 [44], 분산 클러스터링 신뢰도 [40] 등 다양한 전략을 기반으로 권장 시스템에 대한 몇 가지 그래프 클러스터링 기법을 제안했다. 여기서는 그래프 클러스터링 알고리듬이 이 논문의 주요 범위에 속하지 않기 때문에 더 이상 검토하지 않는다. 그러나 그래프 클러스터링의 가장 중요한 측면 중 하나는 클러스터링 알고리듬의 효과를 측정하는 데뿐만 아니라 주어진 그래프에서 관계의 역학에 대한 통찰력을 제공하는 데 중요한 클러스터 품질 평가라는 점에 주목하고 싶다. 효과적인 그래프 클러스터링 메트릭에 대한 자세한 개요는 관심 있는 독자를 참조합니다 [3]. 모든 그래프 클러스터링 알고리듬을 사용할 수 있지만, 우리는 주어진 그래프의 구조적으로 의미 있는 클러스터를 제공하기 때문에 표준 분할 기반 Girvan-Newman 알고리듬[31]을 목적을 위해 사용한다. 기르반-뉴먼 알고리즘은 복잡한 시스템에서 커뮤니티 탐지에 사용되는 직관적이고 잘 알려진 알고리즘이다. 모든 에지가 삭제될 때까지 적절한 에지를 반복적으로 제거하는 글로벌 분할 알고리즘이다. 각 반복에서 연결된 구성 요소를 통해 새로운 클러스터가 나타날 수 있습니다. 이 아이디어는 더 높은 중심성을 가진 가장자리가 두 군집을 연결하는 후보라는 것입니다. 따라서 가장자리 [26]의 간격 중심성 측정은 제거 중인 가장자리를 결정하는 데 사용됩니다. 에지 e에 대한 Betweenness 중심성은 교차하는 노드 쌍 사이의 최단 보행 수로 정의된다. 이 알고리듬의 출력은 노드의 계층적 클러스터링을 코드화하는 덴드로그램이다. 이 알고리즘은 4단계로 구성됩니다.

- 네트워크의 모든 에지에 대한 간격 중심성 계산
- 가장 높은 간격의 가장자리를 제거하고 연결된 각 구성 요소에 대해 클러스터를 생성합니다.
- 탈거의 영향을 받는 모든 에지에 대한 니스를 다시 계산합니다.
- 가장자리가 남지 않을 때까지 2단계부터 반복합니다.
쉽게 말해서 최단 보행수를 기준으로 하여 해당 엣지를 각 노드쌍별이 얼마나 거쳐갔는지를 계산하여 이를 계층적 클러스터링 시키는것이 해당 알고리즘이다.
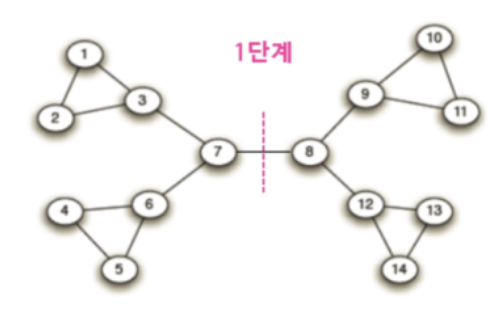
그림을 보면 시각적으로, 직관적으로 보았을 때 대칭적 형태로 4등분 할 수 있을 것만 같은 그래프 구조임을 알 수 있다.({1,2,3}{4,5,6}...) 여기서 이들의 쌍별 최단 보폭으로 엣지를 거쳐갈 때마다 엣지에 값을 +1 하면 위에서 보이듯이 노드 7과 8 사이의 엣지의 값이 직관적으로 가장 클 것이다. 이런 방식으로 7과8 사이의 엣지를 제거하게 되고, 이는 클러스터링과 비슷하다.
4.2 Hierarchical construction

그래프 G와 클러스터링 C={c1,c2,c3…}가 주어지면 각 클러스터는 대표 레이블을 가진 새로운 노드로 요약된다. 이 레이블이 클러스터된 노드와 그 에지에 의해 정의된 하위 그래프에 적용된 임베딩 함수의 결과로 정의될 수 있다고 생각해 보자. 또한 클러스터 간의 연결 비율에 따라 새 노드 간의 에지가 생성됩니다. 즉, 두 클러스터에 의해 정의된 노드 집합 사이에 충분한 연결이 있는 경우에만 에지가 생성됩니다(7행 참조). 마지막으로 새 노드 vCI와 요약된 클러스터 Ci에 속한 모든 노드를 연결하는 계층적 에지가 생성됩니다(12줄 참조). 제안된 계층 구조는 무사비 등이 제안한 것과 유사하다. [50] 그러나 계층적 에지를 통해 클러스터링 알고리즘에 의해 생성된 요약을 명시적으로 포함한다. 따라서 제안된 계층 구조는 원본 그래프와의 관계를 유지하면서 클러스터를 통해 추상 정보를 인코딩하는 표현을 얻는다.
4.3 Hierarchical embedding
이 섹션에서는 그래프의 계층적 정보를 임베딩으로 인코딩하는 새로운 방법을 소개한다. 또한 제안된 기술은 그래프 임베딩 기능에 의해 사용될 수 있다는 점에서 일반적이다.
벡터 공간과 임베딩 함수 u: G! Rn에 매핑되어야 하는 그래프 G가 주어지면, 우리는 먼저 4.2절의 제안된 방법론에 따라 계층적 표현 HG를 얻는다. 따라서 HG는 L레벨을 고려한 추상적 정보로 원본 그래프를 풍부하게 만들었다. 마지막으로 계층적 정보를 사용하여 계층적 임베딩을 구성할 것을 제안한다. 제안된 임베딩의 일반적인 형태는 다중 스케일 및 계층 관계의 그래프를 고려한다. 따라서 임베딩 기능은 서로 다른 추상화 수준에서 노드의 컨텍스트 정보를 압축적으로 인코딩할 뿐만 아니라 계층 축소를 인코딩한다.
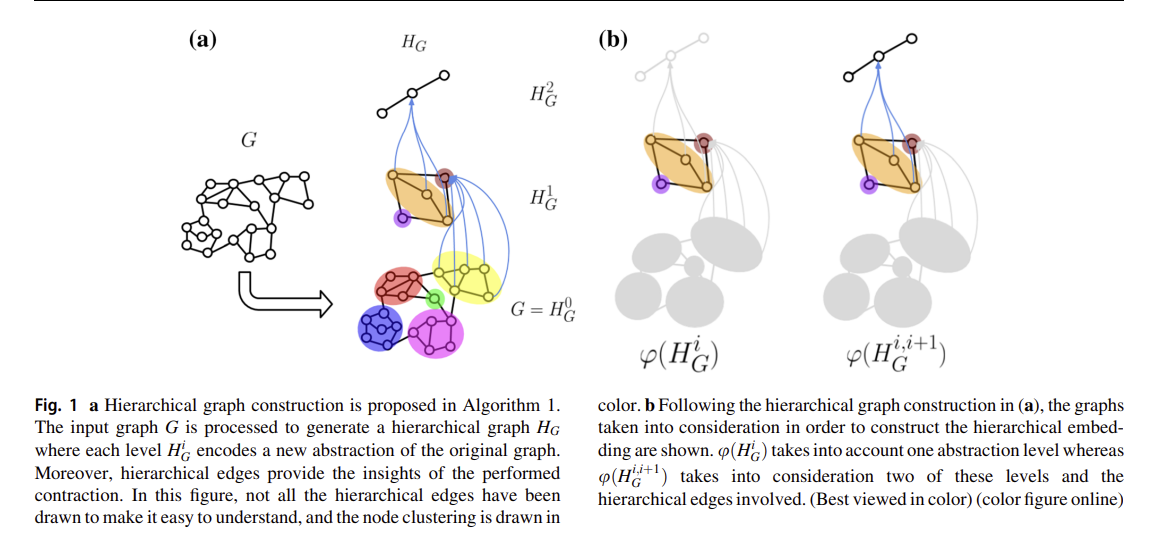
여기서 추가적으로 다양한 방법의 계층적 클러스터링 임베딩 방법이 주어지는데,
Baseline embedding
Pyramidal embedding
Generalized pyramidal embedding
Hierarchical embedding (이걸 사용하는 것 같다. 계층적 에지를 통해 단일 그래프로 간주하여 서로 다른 레벨을 혼합하여 계산된다 그림1b)
Exhaustive embedding
5 Stochastic graphlet embedding
확률적 그래프렛 임베딩(SGE)은 그래프 G를 고차원 벡터 공간 Rn에 명시적으로 임베딩하는 함수u: G -> Rn으로 정의할 수 있다. SGE의 전체 절차는 두 단계로 설명될 수 있으며(그림 2 참조), 첫 번째 단계에서는 G의 그래플릿을 확률적으로 샘플링하고 두 번째 단계에서는 추출된 그래플릿에서 각 동형 그래플릿의 빈도를 근사적이지만 거의 정확한 방식으로 카운트한다. 전체 절차는 제어된 복잡도로 G에서 증가하는 에지 수를 가진 연결된 그래플릿의 정밀한 분포를 가져오는데, 이는 노드로 표현되는 정보와 복잡한 상호 작용 사이의 관계를 가져온다.
5.1 Stochastic graphlets sampling
그래프 G=(V,E,Lv,Le)를 고려할 때, 그래프 추출 절차의 목표는 G에서 에지 수가 증가하는 확률적 그래프렛의 통계를 얻는 것이다. 그래플릿을 추출하는 방법은 확률적이며 최대 정도, 최대 노드 수 등과 같은 토폴로지 또는 구조적 특성을 제한하지 않고 무한히 증가하는 에지 수를 가진 그래플릿을 균일하게 샘플링한다. 알고리즘 2에 설명된 우리의 그래프렛 샘플링 절차는 반복되며 반복 횟수는 샘플링할 뚜렷한 그래프렛의 수를 나타내는 매개 변수 M에 의해 제어된다(알고리즘 2의 2행 참조). 또한, 이러한 M 반복 프로세스 각각은 단일 반복 프로세스가 가져야 하는 최대 반복 횟수를 나타내는 다른 매개 변수 T에 의해 조절됩니다(라인 5 참조). 이러한 각 반복은 현재 구성 중인 그래플릿에 에지를 추가하기 때문에, T는 각 그래플릿이 포함해야 할 최대 에지의 수를 간접적으로 지정한다. Ut와 At를 각각 고려하며, 반복 t까지 방문한 노드와 에지의 집계된 집합으로, 그것들은 각 반복 단계의 시작에서 A0 = {0}, 그리고 V에서 균일하게 샘플링된 무작위로 선택된 노드 u로 U0= {u}로 초기화된다(4줄 참조). 그 후, t번째 반복(t1 사용)에서 샘플링 절차는 임의의 노드 u2 Ut 1에서 연결된 에지(u,v)를 무작위로 선택합니다(7줄 참조). 따라서 프로세스가 업데이트됩니다. 반복 단계 내의 이러한 모든 과정은 최대 T 모서리가 있는 그래플렛을 샘플링하기 위해 T번 반복된다. M은 그래플릿 생성을 통계적으로 의미 있게 만들기 위해 상대적으로 큰 값으로 설정됩니다. 이론적으로, M의 값은 표본 복잡도[81]의 정리에 의해 유도되며, 이는 생물정보학 영역[58, 70]에서 널리 연구되고 사용된다. 그러나 그것에 대한 논의와 증거는 현재 논문의 범위를 벗어납니다. 직관적으로, 이 절에서 설명하는 그래플릿 샘플링 절차는 G를 효율적으로 구문 분석하고 증가하는 에지 수로 원하는 수의 연결된 그래플릿을 추출하는 재시작과 함께 무작위 보행 프로세스를 따른다. 이 알고리듬은 주어진 그래프에서 연결된 그래플릿을 샘플링할 수 있지만 정확한 방법으로 추출하는 값비싼 방법은 피한다. 여기서 가설은 충분한 수의 그래플릿이 샘플링되면 경험적 분포가 그래프에서 그래플릿의 실제 분포에 가까울 것이라는 것이다. 또한, 상기 공정에서, 1부터 T까지의 다양한 에지 수를 갖는 MT 그래플릿을 추출할 수 있다는 점에 유의해야 한다.

5.2 Hashed graphlets distribution
G로부터 추출된 그래플릿의 분포를 얻기 위해서는 샘플링된 그래플릿에서 동형 그래플릿의 집합을 식별한 다음 각 동형 집합의 카디널리티를 계수해야 한다. 그렇게 하는 사소한 방법은 분명히 그들 사이에 존재할 수 있는 가능한 파티션을 감지하기 위해 가능한 모든 그래프 쌍에 대한 그래프 동형을 확인하는 것이다. 그럼에도 불구하고, 그래프 동형화는 일반 그래프에 대한 GI 완료 문제[49]이므로, 앞에서 언급한 방식은 많은 모서리가 있는 많은 수의 그래플릿을 샘플링하기 때문에 비용이 매우 많이 든다. 동형 그래플렛을 분할하는 대안적이고 효율적이며 근사적인 방법은 그래프 해싱이다. 그래프의 로컬 및 홀리스틱 위상 특성을 기반으로 그래프를 해시 코드(실수의 시퀀스)로 매핑하는 매핑 h: G! Rm으로 정의할 수 있는 그래프 해시 함수입니다. 이상적인 그래프 해시 함수는 두 개의 동형 그래프를 동일한 해시 코드에 매핑해야 하며 두 개의 비동형 그래프를 두 개의 다른 해시 코드에 매핑해야 한다. 두 동형 그래프가 동일한 해시 코드를 가져야 한다는 조건을 만족시키는 해시 함수를 설계하는 것은 쉽지만, 모든 비동형 그래프 쌍에 대해 서로 다른 해시 코드를 보장하는 해시 함수를 찾는 것은 매우 어렵다. 대안은 충돌 확률이 낮은 그래프 해시 함수를 설계하는 것이다. 즉, 두 개의 비동형 그래프를 매우 낮은 확률로 동일한 해시 코드에 매핑하는 것이다. 그래프 해시의 주요 목적은 그래프 해시의 분포를 계산하고 정량화하기 위해 G에서 추출된 그래플렛을 동형 그래프렛의 해당 하위 집합(일명 파티션 인덱스 또는 히스토그램 빈)에 할당하는 것이다. 알고리즘 3에 설명된 균일하게 샘플링된 그래플릿의 분포를 얻기 위해 제안된 메커니즘은 그래프 해시 함수에 의해 생성된 그래플릿 g의 해시 코드에 해당하는 단일 엔트리를 갖는 전역 해시 테이블 H를 유지한다. H는 알고리즘이 새로운 그래프 해시 코드에 맞서고 시스템이 접하는 모든 고유 해시 코드를 유지함에 따라 점진적으로 성장한다. 각 위치는 파티션 인덱스 또는 히스토그램 빈에 해당하기 때문에 각 고유 해시 코드의 위치는 고정된 상태로 유지된다는 점에 유의해야 한다. 이제 주어진 그래프 g를 해당 히스토그램 빈에 할당하기 위해 해시 코드 h(g)가 해시 테이블 H의 인덱스에 매핑되며, 해당 그래프 해시 코드는 h(g)로 적중한다(행 8 참조). 만약 h(g)가 H에 존재하지 않는다면, 시스템에 의해 발견되고 H의 끝에 h(g)가 추가되는 새로운 해시 코드(그래플렛)로 간주된다.
5.3 Hierarchical stochastic graphlet embedding
본 연구에서는 제안된 확률적 그래프렛 임베딩의 특성을 이전 섹션에서 소개한 계층적 임베딩과 결합할 것을 제안한다. 한편, SGE는 관련된 가장자리 수를 변화시키는 국소 구조에 대한 통계 정보를 제공한다. 따라서 너무 시끄러운 데이터를 처리할 수 없는 그래프의 세밀한 통찰력을 제공한다. 그래프 계층 구조에서 제공하는 추상화를 사용하면 글로벌 그래프 정보에 대한 통찰력을 제공할 수 있는 거친 정보로 이동하는 각 그래플렛의 수용 필드가 증가한다. 또한, 계산 중에 계층적 에지를 사용하면 일부 수준에서 정보를 결합할 수 있다. 즉, 서로 다른 수준의 세부 정보를 결합할 수 있다(등식 (1) 참조). 일단, 우리는 이 임베딩을 계층적 확률적 그래프 임베딩(HSGE)으로 나타낼 것이다.
result