[알고리즘] Quick Sort

Emily·2020년 10월 24일

알고리즘

목록 보기

3/8

Abstract

Quick Sort는 분할 정복(Divide and Conquer) 방법을 통해 주어진 배열을 정렬한다.
다른 원소와의 비교만으로 정렬을 수행하는 비교 정렬이다.
배열을 비균등하게 분할한다.

Divide and Conquer
문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략

Process(Ascending)

배열에서 하나의 원소를 고른다. ➡ 피벗(pivot)

피벗 앞에는 피벗 보다 작은 모든 원소들이 오고, 뒤에는 큰 원소들이 오도록 피벗을 기준으로 배열을 둘로 나눈다.
분할을 마친 뒤에 피벗은 더 이상 움직이지 않는다.

분할된 두 개의 작은 배열에 대해 재귀적으로 이 과정을 반복한다.
재귀 호출이 한 번 진행될 때마다 최소한 하나의 원소는 최종 위치가 정해지므로, 알고리즘이 반드시 끝난다는 것을 보장할 수 있다.

C++ Code(Ascending)

Quick Sort는 Divide와 Conquer로 이루어져 있다.

정복 (Conquer)

부분 배열을 정렬한다.
순환 호출을 이용하여 다시 분할 정복 방법을 적용한다.

void quickSort(int arr[], int left, int right){
  if(left >= right) return;
  
  int pivot = partition(arr, left, right); // 분할

  // pivot을 제외한 2개의 부분 배열을 대상으로 순환 호출
  quickSort(arr, left, pivot-1);  // left Conquer
  quickSort(arr, pivot+1, right); // right Conquer
}

분할 (Divide)

입력 배열을 피벗 기준으로 비균등하게 2개의 부분 배열로 분할한다.
피벗을 중심으로 왼쪽은 작은 요소들, 오른쪽은 큰 요소들이 오게 한다.

int partition(int arr[], int left, int right){
  int mid = (left + right) / 2;
  swap(arr[left], arr[mid]);

  int pivot = arr[left]; //가장 왼쪽 값을 pivot으로 설정
  int i = left, j = right;

  while(i<j){
    while(pivot < arr[j]){ //오른쪽부터 작은 값을 찾는다.
      j--;
    }
    while(i<j && pivot >= arr[i]){ //왼쪽부터 큰 값을 찾는다.
      i++;
    }
    swap(arr[i], arr[j]); //교환
  }

  arr[left] = arr[i];
  arr[i] = pivot;
  return i;
}

Quick Sort 개선

partition()에서 피벗 값이 최소나 최대값으로 지정되어 파티션이 나누어지지 않을 때, O(n^2)에 대한 시간복잡도를 가진다.
즉, 배열이 오름차순 또는 내림차순으로 정렬되어 있는 경우에 O(n^2)를 갖게 된다.
배열에서 가장 앞에 있는 값과 중간 값을 교환한다면, 확률적으로 시간복잡도를 O(nlog₂n)으로 개선할 수 있다.
하지만 이 방법으로도 Worst case의 시간복잡도를 O(nlog₂n)로 만들 수 없다.

GIF로 이해하는 Quick Sort

시간복잡도

Best case : T(n) = O(nlog₂n)

비교횟수 : log₂n
레코드의 개수 n이 2의 거듭제곱이라고 가정했을 때, n = 2^k라고 표현할 수 있다.
n = 2^3의 경우, 2^3 -> 2^2 -> 2^1 -> 2^0 순으로 줄어들어 순환 호출의 깊이가 3이다.

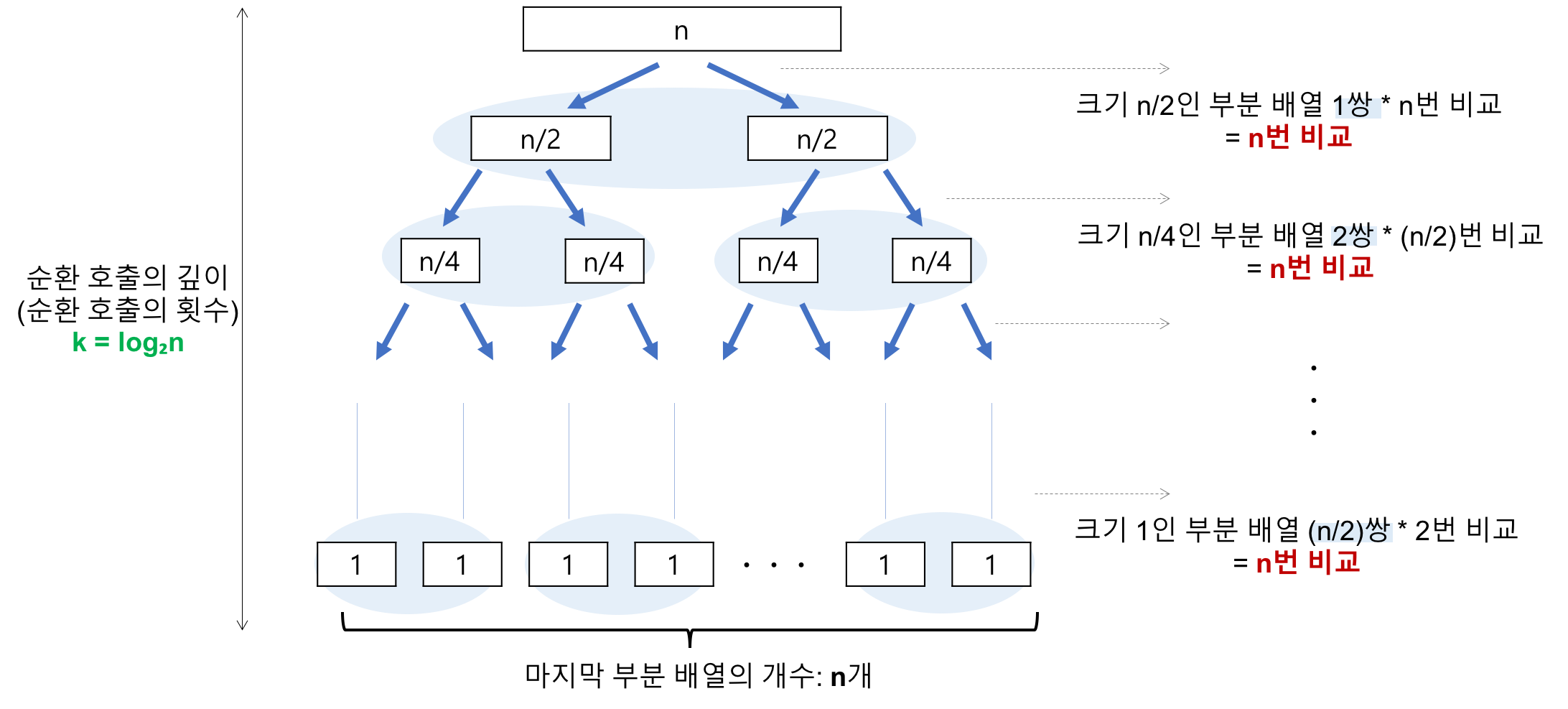
이를 일반화 하면, n = 2^k 이므로 호출의 깊이는 k이다.
이 때, k = log₂n 이므로 비교횟수는 log₂n 이다.
각 순환 호출 단계의 비교 연산 : n
각 순환 호출에서 전체 리스트의 거의 모든 레코드를 비교해야 하므로 평균 n번 정도의 비교가 발생한다.

따라서 Best case의 시간복잡도는 순환 호출의 깊이 * 각 순환 호출 단계 비교 연산 = nlog₂n가 된다.

Worst case : T(n) = O(n^2)

최악의 경우 : 배열이 이미 정렬되어 있는 경우

비교횟수 : n

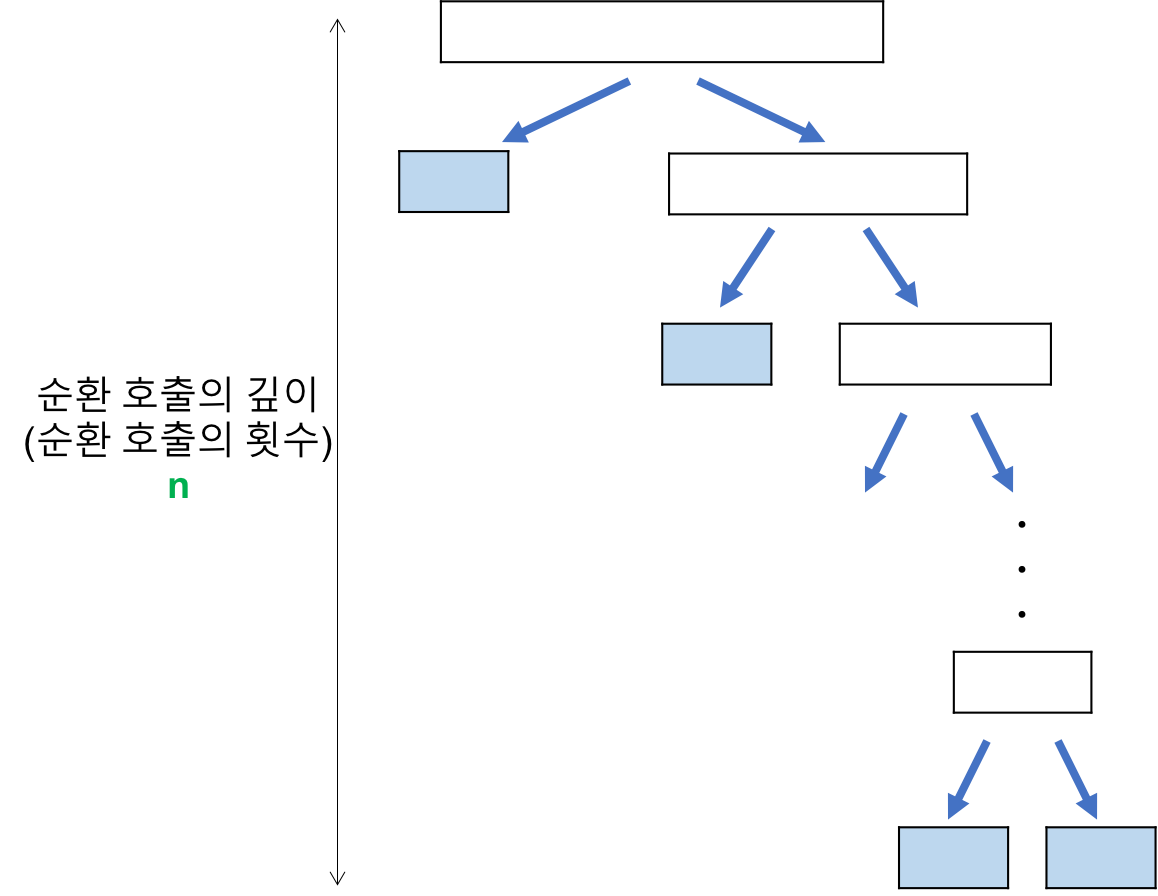
레코드의 개수 n이 2의 거듭제곱이라고 가정했을 때, n = 2^k라고 표현할 수 있다. 이 때, 순환 호출의 깊이는 n이다.
각 순환 호출 단계의 비교 연산 : n
각 순환 호출에서는 전체 리스트의 대부분 레코드를 비교해야 하므로 평균 n번 비교한다.