[알고리즘] 정리

Radix Sort

낮은 자리수부터 비교하여 정렬해 간다는 것을 기본 개념으로 하는 정렬 알고리즘
비교 연산을 하지 않으며 정렬 속도가 빠르다.
데이터 전체 크기에 Radix Table 크기의 메모리가 더 필요하다.

정렬 방식

1. 0~9 까지의 Bucket(Queue 자료구조의)을 준비한다.
2. 모든 데이터에 대하여 가장 낮은 자리수에 해당하는 Bucket에 차례대로 데이터를 둔다.
3. 0부터 차례대로 버킷에서 데이터를 다시 가져온다.
4. 가장 높은 자리수를 기준으로 하여 자리수를 높여가며 2번 3번 과정을 반복한다.

예시

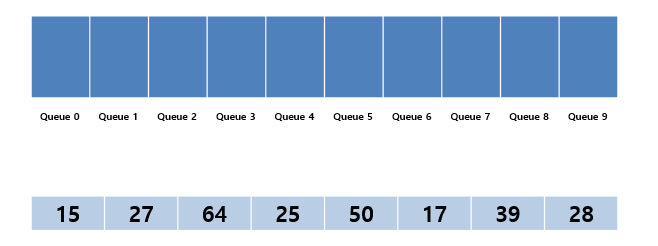
각 숫자에 해당하는 큐 공간을 할당하고 진행한다.

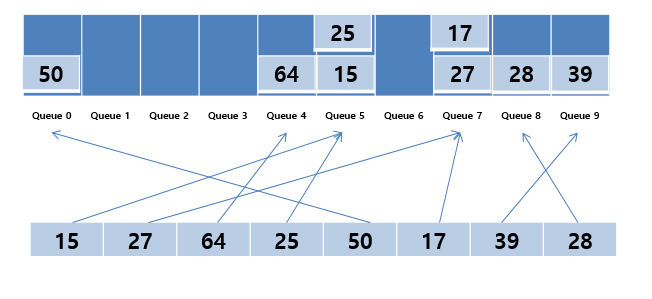
먼저 1의 자리 숫자부터 시도한다. 데이터 순서대로 각 1의 자리에 해당되는 Queue에 데이터가 들어가게 된다. 15같은 경우는 1의 자리가 5이므로 Queue 5에 들어가는 방식이다.

1의 자리 정렬이 완료되면, 10의 자리에 대해 같은 작업을 반복한다.

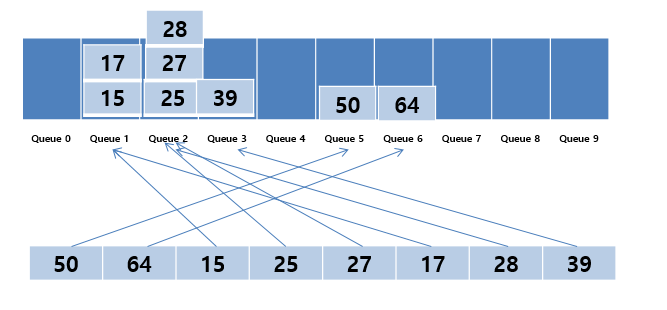
각 데이터의 10의 자리에 해당되는 큐에 데이터를 위치시킨다.
0번 큐부터 차례대로 데이터를 가지고 온다.

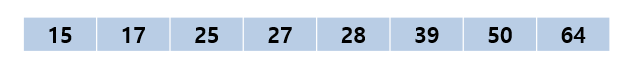
최종 정렬이 완료된다.

특징

시간복잡도는 O(dn). d는 가장 큰 숫자의 자리수
자리수가 고정되어 있어서 안정성이 있다.

위상정렬 (Topological sort)

방향 그래프에 존재하는 각 정점들의 선행 순서를 위배하지 않으면서 모든 정점을 나열하는 것.

하나의 방향 그래프에는 여러 위상 정렬이 가능하다.
위상 정렬의 과정에서 선택되는 정점의 순서를 위상 순서(Topological Order)라고 한다.
위상 정렬의 과정에서 그래프에 남아있는 정점 중에 진입 차수가 0인 정점이 없다면, 위상 정렬 알고리즘이 중단되고, 이러한 그래프로 표현된 문제는 실행이 불가능한 문제가 된다.

위상정렬을 이용한 기본적인 해결 방법

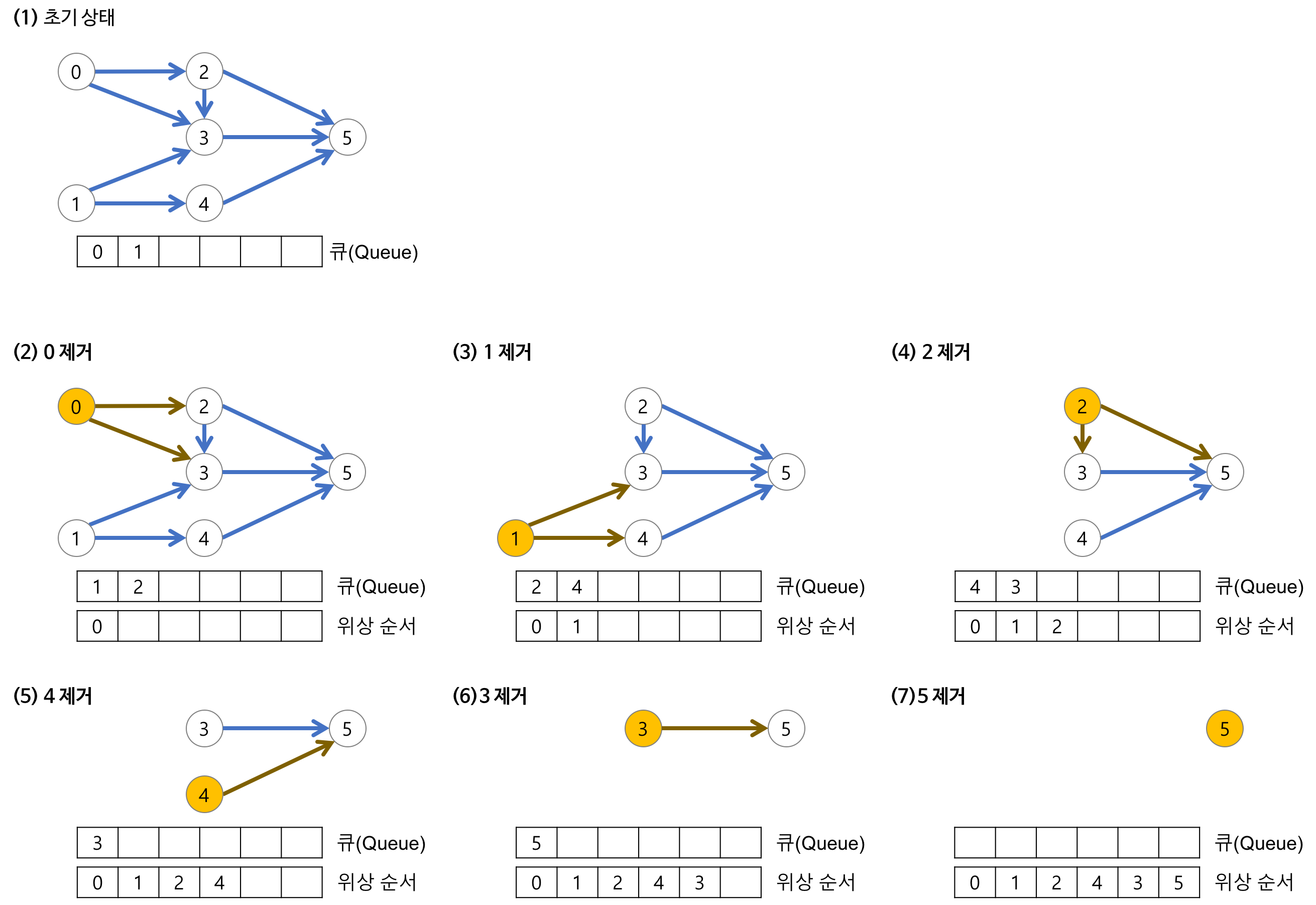
1. 진입 차수가 0인 정점(즉, 들어오는 간선의 수가 0)을 선택한다.
   진입 차수가 0인 정점이 여러 개 존재할 경우 어느 정점을 선택해도 무방하다.
   초기에 간선의 수가 0인 모든 정점을 큐에 삽입한다.
2. 선택된 정점과 여기에 부속된 모든 간선을 삭제한다.
   선택된 정점을 큐에서 삭제한다.
   선택된 정점에 부속된 모든 간선에 대해 간선의 수를 감소한다.
3. 위의 과정을 반복해서 모든 정점이 선택, 삭제되면 알고리즘 종료한다.

허프만 코드

가변 길이 코드를 만들어서 효율적으로 압축한다.

예제

문자열 "ABBCCCDDDDEEEEEFFFFFF"의 가변 길이 코드 만들기

1. 알파벳 별 빈도수를 저장한 노드를 생성한다.
   

2. 빈도수를 비교하여 노드를 만든다.
   가장 작은 빈도수를 가진 노드와 두 번째로 작은 빈도수의 노드를 합쳐 노드를 만든다.
   

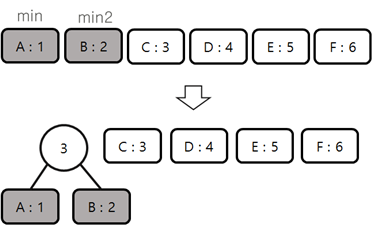
3. 2를 반복한다.
   

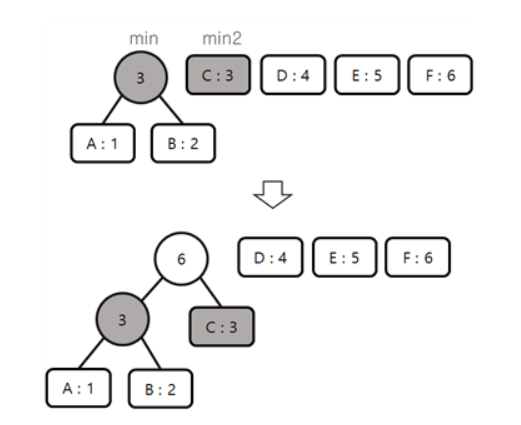
결과

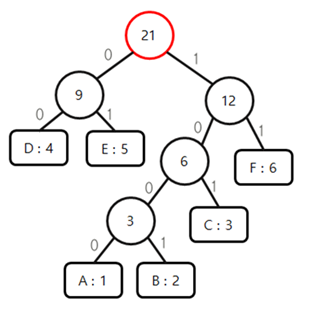
만들어진 허프만 코드를 가지고 문자열을 인코딩한다.

참고 사이트

Radix Sort
위상 정렬
허프만 코드