[알고리즘] 그림으로 알아보는 힙정렬(Heap Sort)

힙 자료구조에 이어 힙정렬에 대해 포스팅 해보겠습니다. 이전 포스팅에서 작성한 코드를 기준으로 작성하겠습니다.

힙정렬의 시간복잡도는 $O(NlogN)$으로 빠른 정렬에 속합니다. 퀵정렬은 최악의 경우 $O(N^2)$의 성능을 내지만, 힙정렬은 안정적인 성능을 발휘한다고 합니다. 또한 추가적인 배열을 사용하지 않아 메모리 측면에서도 이점을 보입니다.

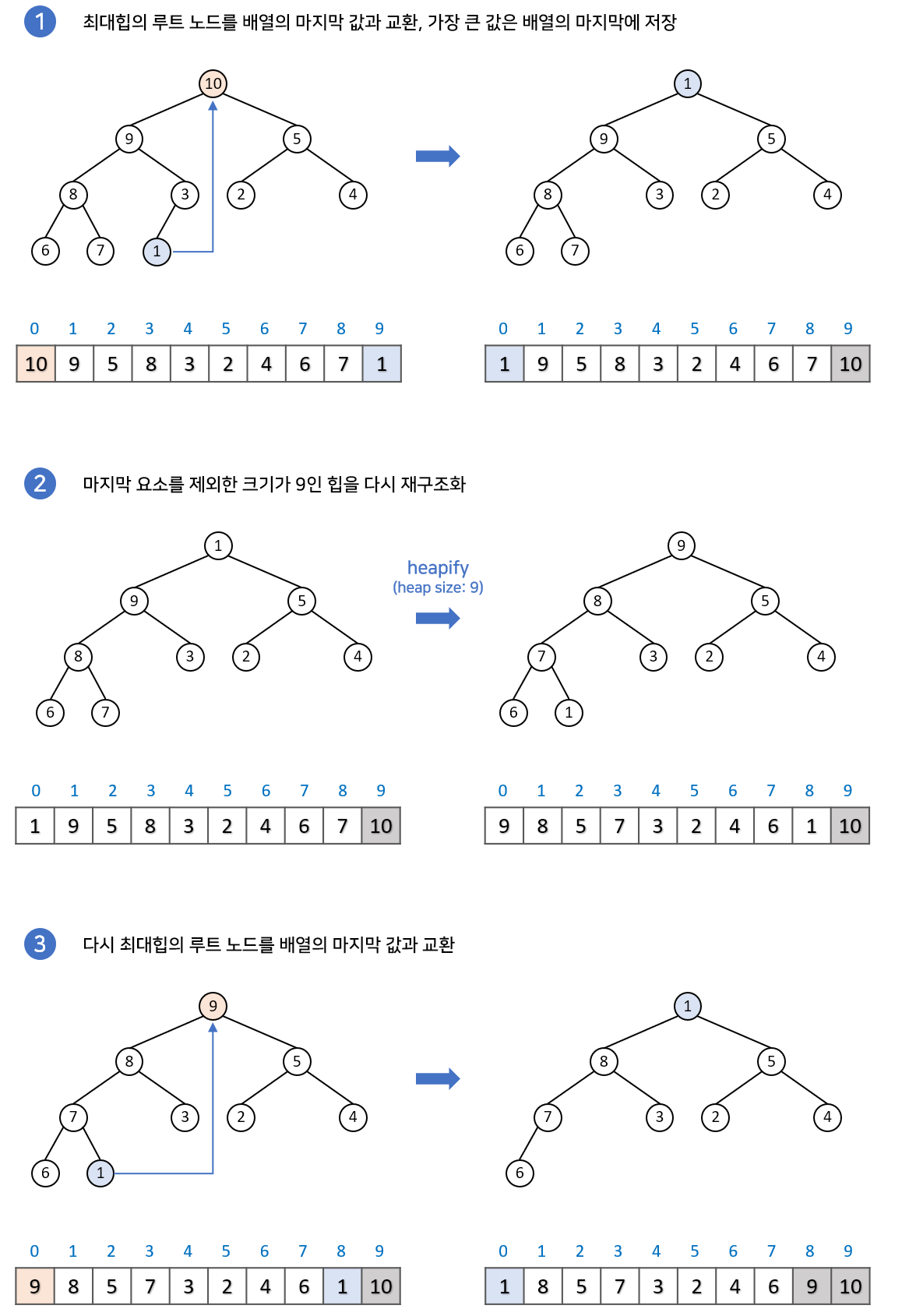
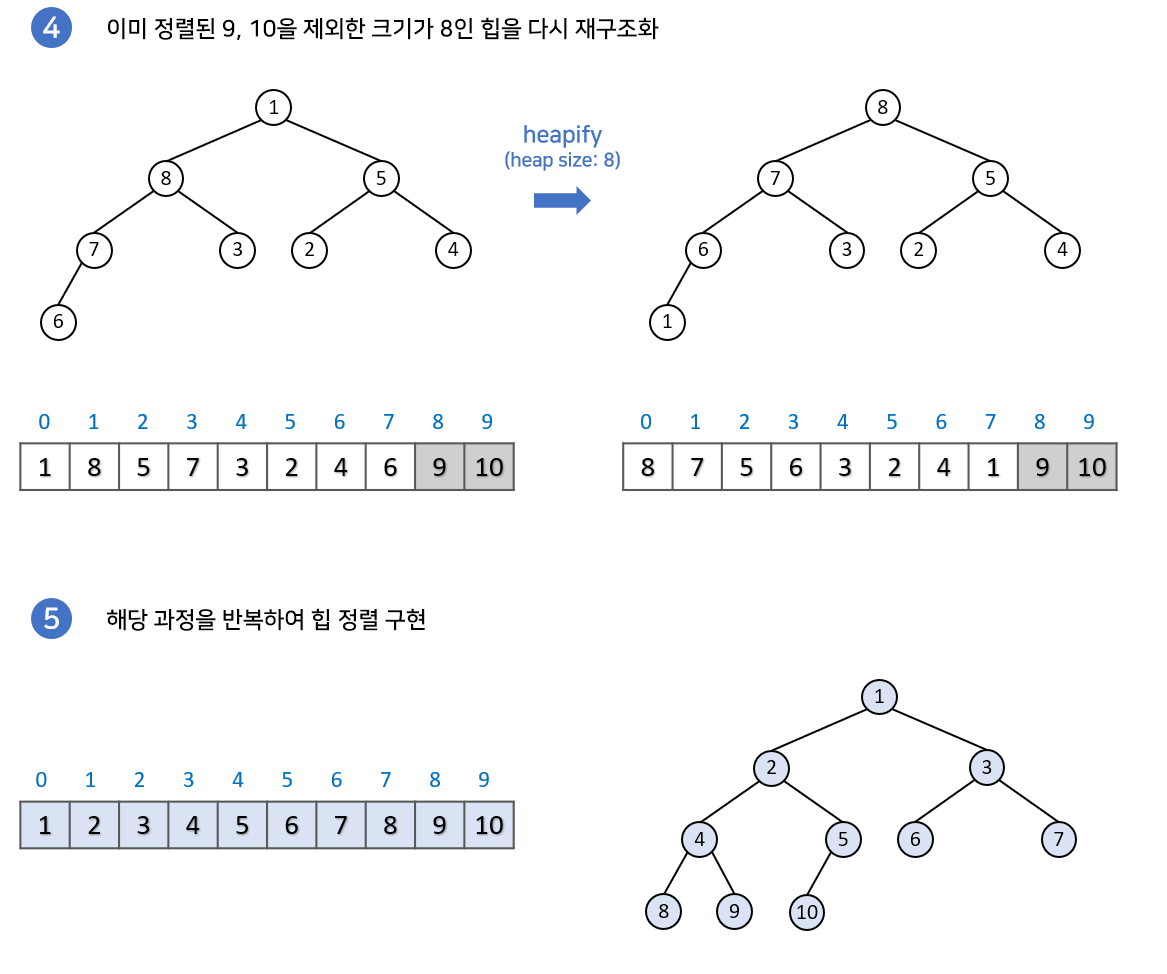
구현과정

힙정렬은 삽입보다는 삭제과정만 이루어진다고 생각하시면 편합니다. 최대힙을 구현한 뒤, 루트노드 삭제하여 배열의 맨 마지막에 넣어주고, 깨진 힙을 재구조화하는 과정을 반복하면 힙정렬을 구현할 수 있습니다.

코드

이전 힙 포스팅 중 down heapify 재귀함수 코드로 구현하면 다음과 같습니다.

    def down_heap(array, index, heap_size):
            parent = index
            left_child = 2 * parent + 1
            right_child = 2 * parent + 2

            if left_child < heap_size and array[left_child] > array[parent]:
                parent = left_child
            if right_child < heap_size and array[right_child] > array[parent]:
                parent = right_child
            if parent != index:
                array[parent], array[index] = array[index], array[parent]
                make_heap(array, parent, heap_size)

    # 부모노드가 되는 노드들만을 골라서 뒤에서부터 heapify를 차례로 실행
    for root in range((N - 1) // 2, -1, -1):
        make_heap(array, i, heap_size)

    # 힙 정렬 수행
    for i in range(N - 1, 0, -1):
    	array[0], array[i] = array[i], array[0]
        down_heap(array, 0, i - 1)