
Longest Common Subsequence? Substring?
LCS는 주로 최장 공통 부분수열(Longest Common Subsequence)을 말합니다만, 최장 공통 문자열(Longest Common Substring)을 말하기도 합니다.
문자열 ABCDEF와 GBCDFE를 이용하여 차이점을 예시로 들어보면

해당 예시에서 최장 공통 부분수열(Longest Common Subsequence)은 BCDF, BCDE가 될 수 있습니다. 부분수열이기 때문에 문자 사이를 건너뛰어 공통되면서 가장 긴 부분 문자열을 찾으면 됩니다. 최장 공통 문자열(Longest Common Substring)은 BCD입니다. 부분문자열이 아니기 때문에 한번에 이어져있는 문자열만 가능합니다.
최장 공통 문자열(Longest Common Substring)
최장 공통 부분수열(Longest Common Subsequence)을 구하기 전에 최장 공통 문자열(Longest Common Substring)을 먼저 보도록 하겠습니다. 해당 과정이 더 쉽고, 최장 공통 부분수열(Longest Common Subsequence)을 구하는데 사용되기 때문에 먼저 알아보겠습니다.
점화식
if i == 0 or j == 0: # 마진 설정
LCS[i][j] = 0
elif string_A[i] == string_B[j]:
LCS[i][j] = LCS[i - 1][j - 1] + 1
else:
LCS[i][j] = 0최장 공통 문자열의 점화식을 코드로 작성해보았습니다. LCS라는 2차원 배열을 이용하여 두 문자열을 행, 열에 매칭합니다. 편의상 i, j가 0일때는 모두 0을 넣어줘 마진값을 설정합니다. 이후 i, j가 1이상일 때부터 검사를 시작합니다. 검사 순서는 다음과 같습니다.
- 문자열A, 문자열B의 한글자씩 비교해봅니다.
- 두 문자가 다르다면
LCS[i][j]에0을 표시합니다. - 두 문자가 같다면
LCS[i - 1][j - 1]값을 찾아+1합니다. - 위 과정을 반복합니다.
위 과정이 성립하는 이유는 공통 문자열은 연속되야 하기 때문입니다. 현재 두 문자가 같을때 두 문자의 앞 글자까지가 공통 문자열이라면 계속 공통 문자열이 이어질 것이고, 아니라면 본인부터 다시 공통 문자열을 만들어 가게 될 것입니다. 아래 예시를 통해 직관적으로 확인할 수 있습니다.
구현과정

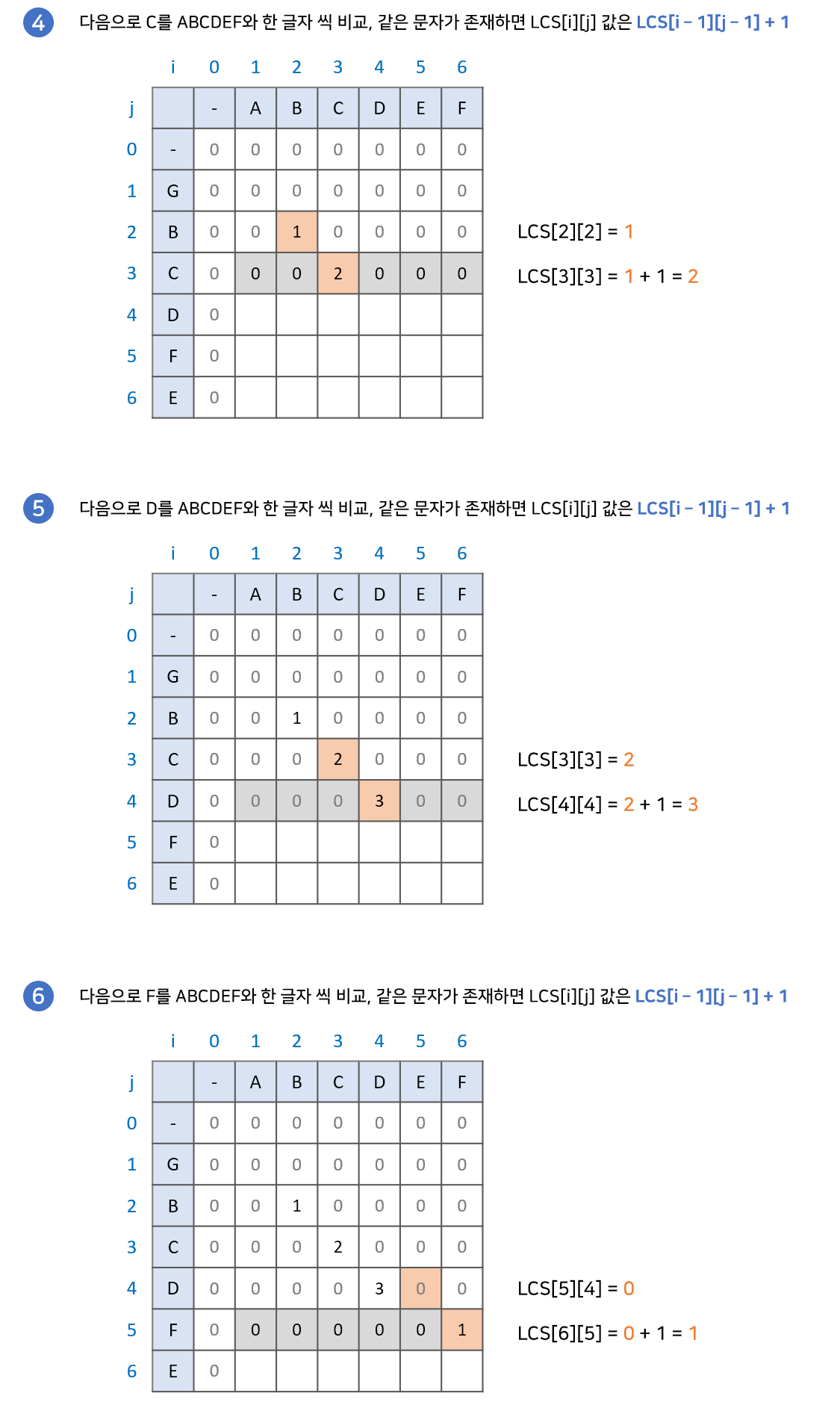
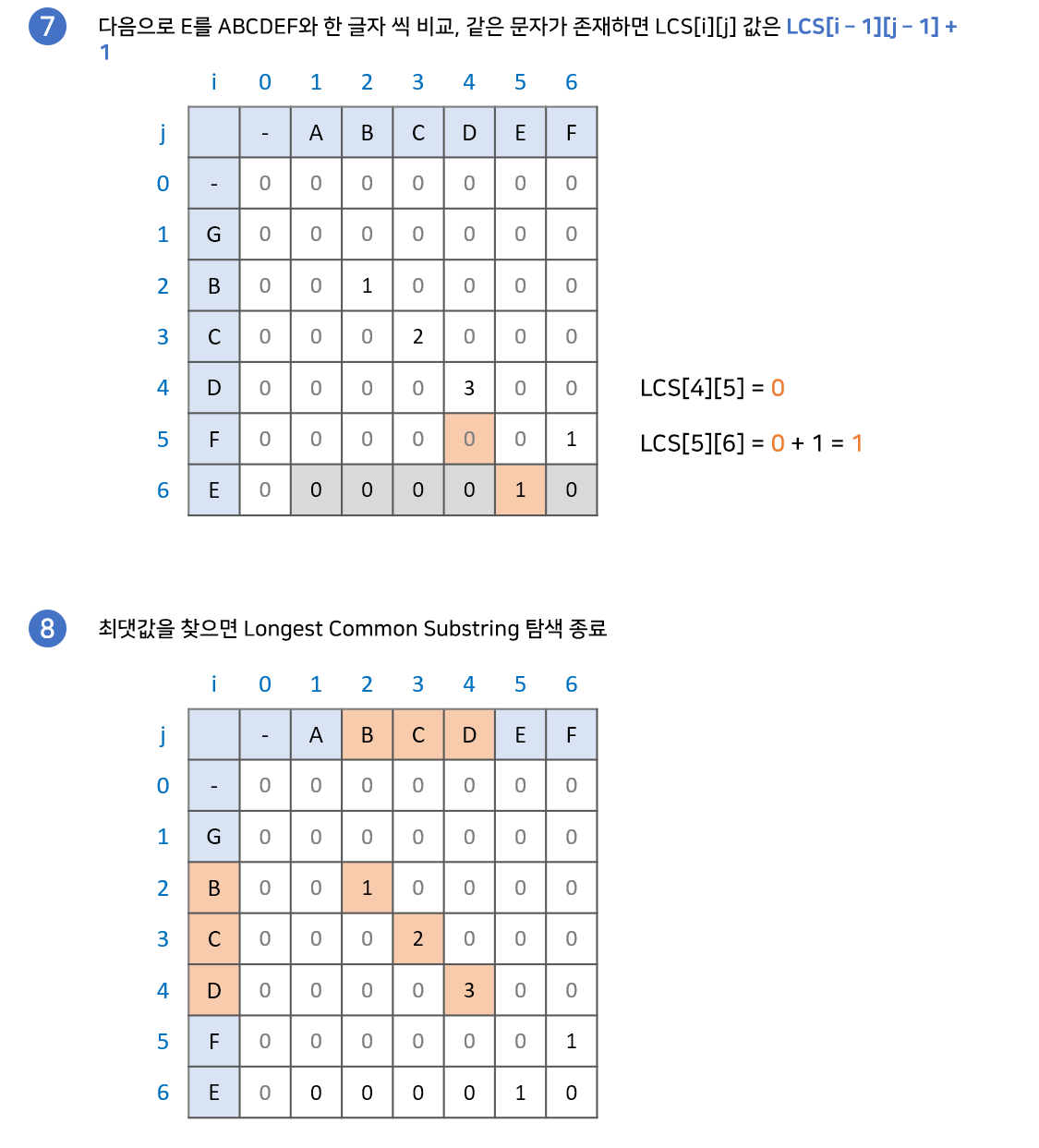
최장 공통 부분수열(Longest Common Subsequence) 길이 구하기
그렇다면 이번에는 다른 LCS인 최장 공통 부분수열(Longest Common Subsequence)를 만들어 보겠습니다.
점화식
if i == 0 or j == 0: # 마진 설정
LCS[i][j] = 0
elif string_A[i] == string_B[j]:
LCS[i][j] = LCS[i - 1][j - 1] + 1
else:
LCS[i][j] = max(LCS[i - 1][j], LCS[i][j - 1])최장 공통 부분수열의 점화식을 코드로 작성해보았습니다. 위와 마찬가지로 LCS라는 2차원 배열에 매칭하고 마진값을 설정한 후 검사합니다.
- 문자열A, 문자열B의 한글자씩 비교해봅니다.
- 두 문자가 다르다면
LCS[i - 1][j]와LCS[i][j - 1]중에 큰값을 표시합니다. - 두 문자가 같다면
LCS[i - 1][j - 1]값을 찾아+1합니다. - 위 과정을 반복합니다.
최장 공통 문자열을 구하는 과정과 다른부분은 비교하는 두 문자가 다를 때 입니다. 비교하는 두 문자가 같을 때는 같은 과정을 보여줍니다. 왜 어떤 부분은 다른 로직을, 어떤부분은 같은 로직을 사용하는지 상세히 살펴보겠습니다.
1. LCS[i - 1][j]와 LCS[i][j - 1]는 어떤 의미인가?
부분수열은 연속된 값이 아닙니다. 때문에 현재의 문자를 비교하는 과정 이전의 최대 공통 부분수열은 계속해서 유지됩니다. '현재의 문자를 비교하는 과정' 이전의 과정이 바로 LCS[i - 1][j]와 LCS[i][j - 1]가 됩니다.
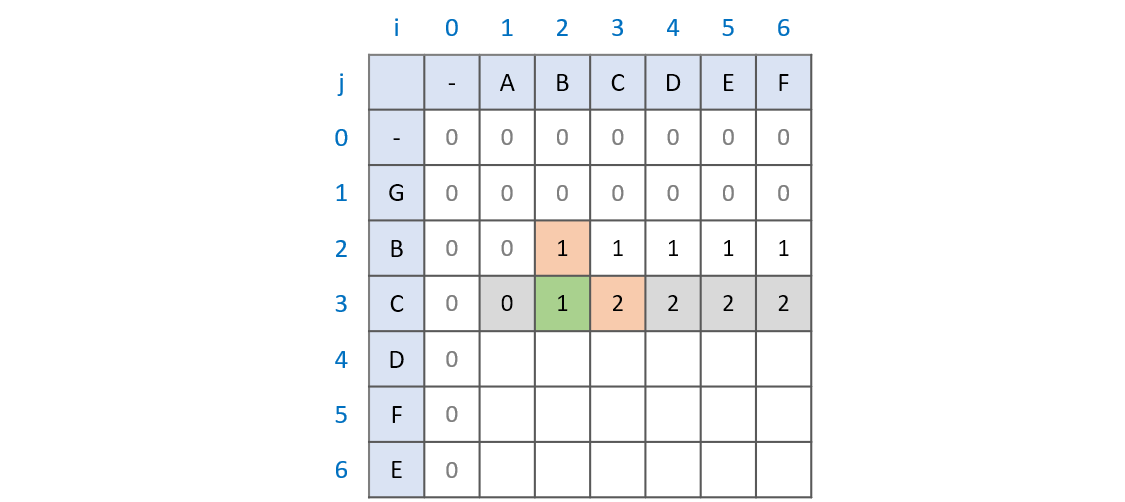
문자열 AB와 GBC를 비교(위 그림의 초록색 부분)하는 과정을 예로 들어보겠습니다. AB와 GBC의 최대 공통 부분수열이 B라는 것을 알기 위해서는 문자열 A와 GBC를 비교하는 과정, 문자열 AB와 GB를 비교하는 과정이 필요합니다. 문자열 AB와 GB의 비교 과정에서 최대 공통 부분수열이 B임을 확인했기 때문에 문자열 AB와 GBC의 최대 공통 부분수열 역시 B가 되는 것입니다.

2. 왜 문자가 같으면 LCS[i][j] = LCS[i - 1][j - 1] + 1인가?
최대 공통 문자열을 구할 때 비교하는 문자가 같으면 LCS[i][j] = LCS[i - 1][j - 1] + 1의 과정을 거쳤습니다. 이 과정이 어떻게 최대 공통 부분수열에도 똑같이 적용될까요? 부분수열이 연속될 필요가 없음을 위 과정에서 여러번 보았습니다. 그렇다면 답은 간단합니다. 두 문자가 같은 상황이 오면 지금까지의 최대 공통 부분수열에 1을 더해주는 것 입니다.
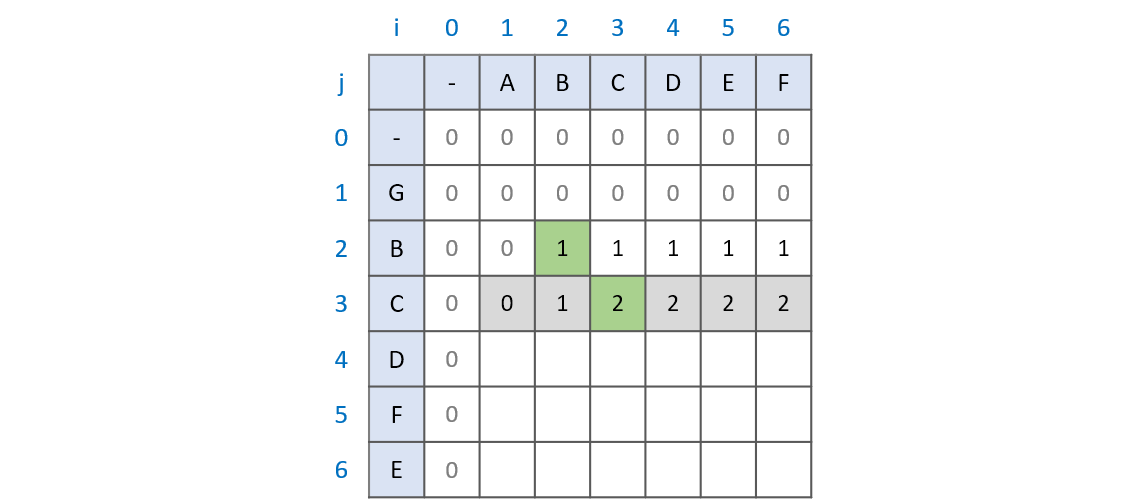
문자열 ABC와 GBC를 비교(위 그림의 초록색 부분)하는 과정을 예로 들어보겠습니다. LCS 배열은 LCS[i - 1][j]와 LCS[i][j - 1]의 비교를 통해 언제나 본인까지의 최대 공통 부분수열 값을 가지고 있습니다. 문자열 AB와 GB를 비교할때와 문자열 ABC와 GBC를 비교할 때 달라진 점은 두 문자열 모두에 C가 추가된 점입니다. 때문에 기존의 최대 공통 부분수열인 B에 C를 더한 BC가 최대 공통 부분수열이 되는 것입니다.

구현과정
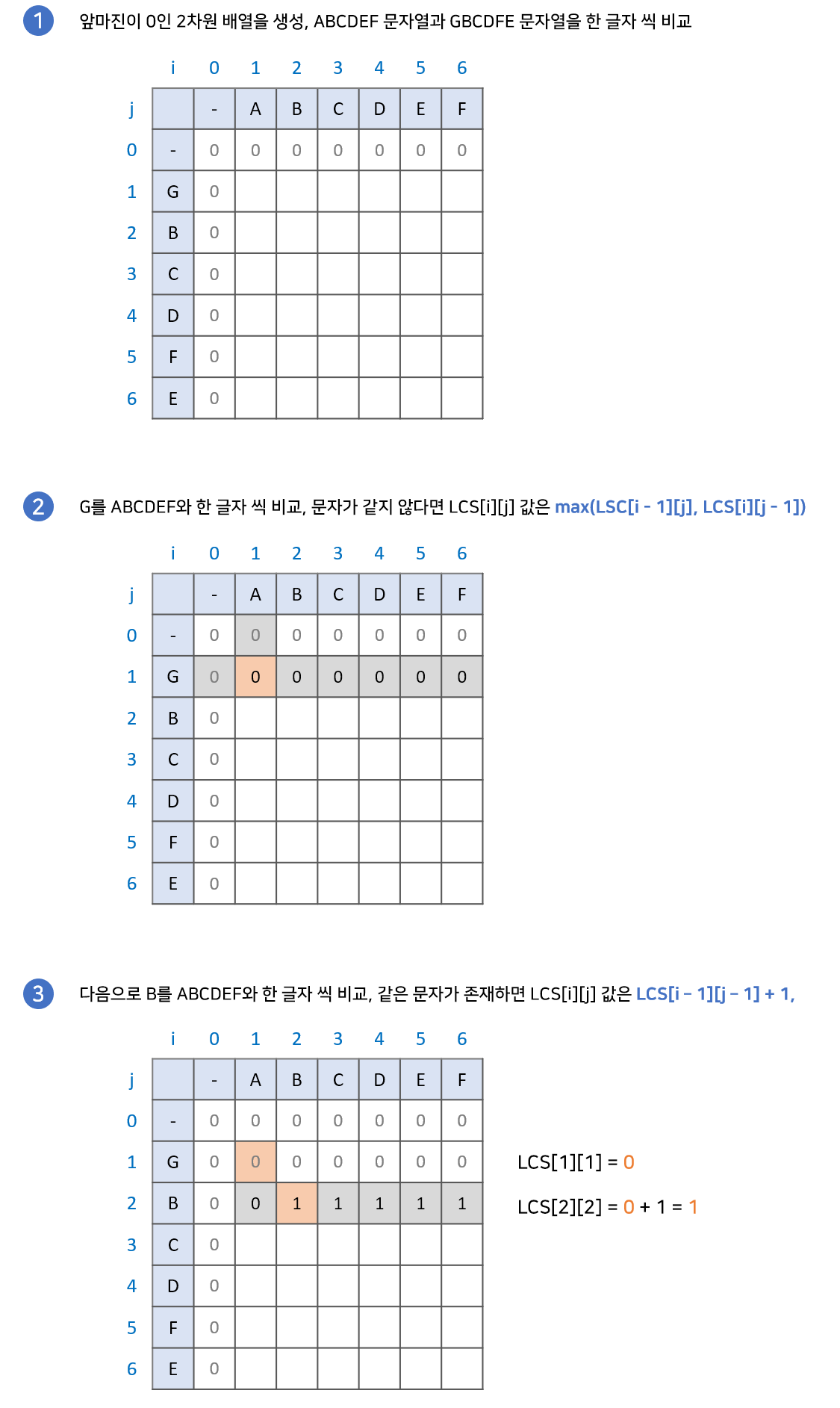
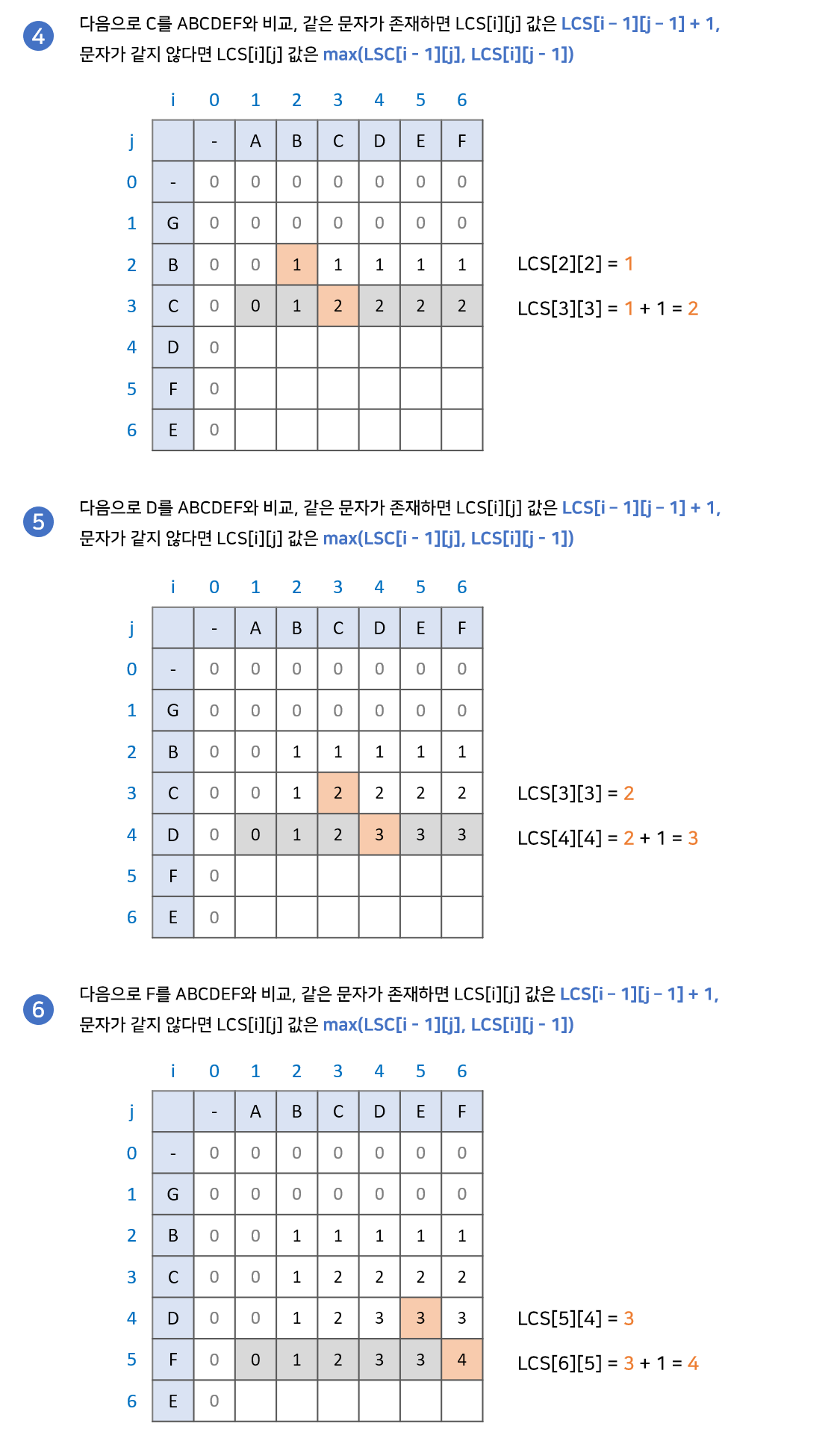

최장 공통 부분수열(Longest Common Subsequence) 찾기
위에서 LCS 구현과정을 통해 LCS 배열을 만들며 LCS의 길이를 알았습니다. 이제 만든 LCS 배열을 이용해 최장 공통 부분수열의 값을 찾아보겠습니다. 경우에 따라 여러가지 답이 나올 수 있기 때문에 아래 예시는 한가지 경우만을 보겠습니다.
과정은 다음과 같습니다.
- LCS 배열의 가장 마지막 값에서 시작합니다. 결과값을 저장할
result배열을 준비합니다. LCS[i - 1][j]와LCS[i][j - 1]중 현재 값과 같은 값을 찾습니다.
2-1. 만약 같은 값이 있다면 해당 값으로 이동합니다.
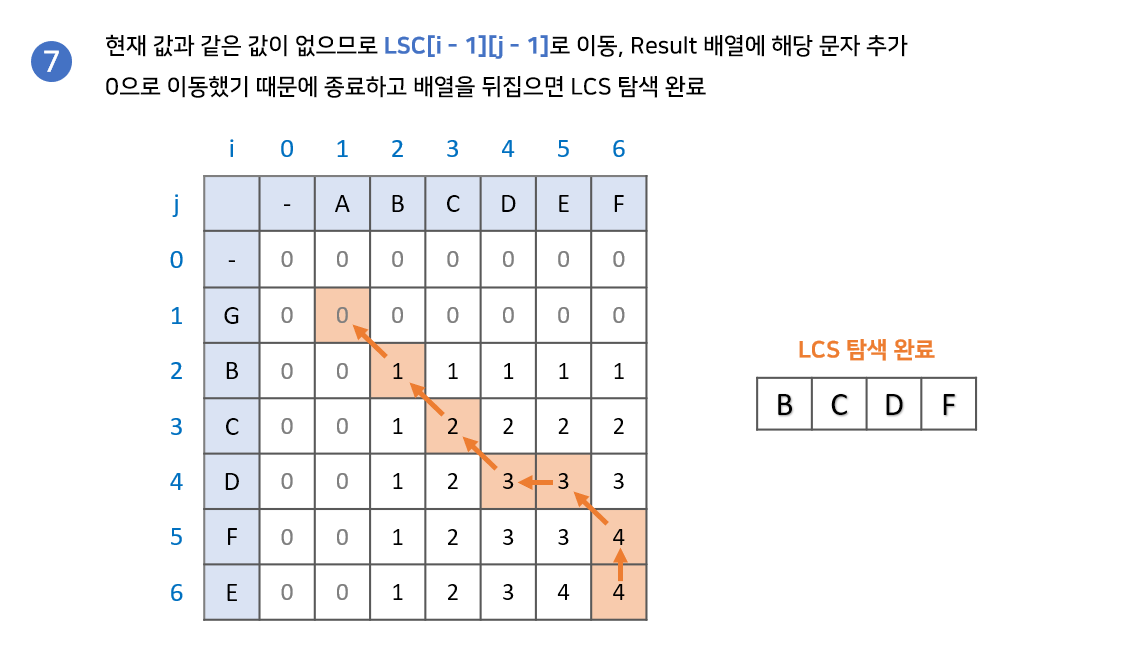
2-2. 만약 같은 값이 없다면result배열에 해당 문자를 넣고LCS[i -1][j - 1]로 이동합니다.- 2번 과정을 반복하다가 0으로 이동하게 되면 종료합니다.
result배열의 역순이 LCS 입니다.
구현과정
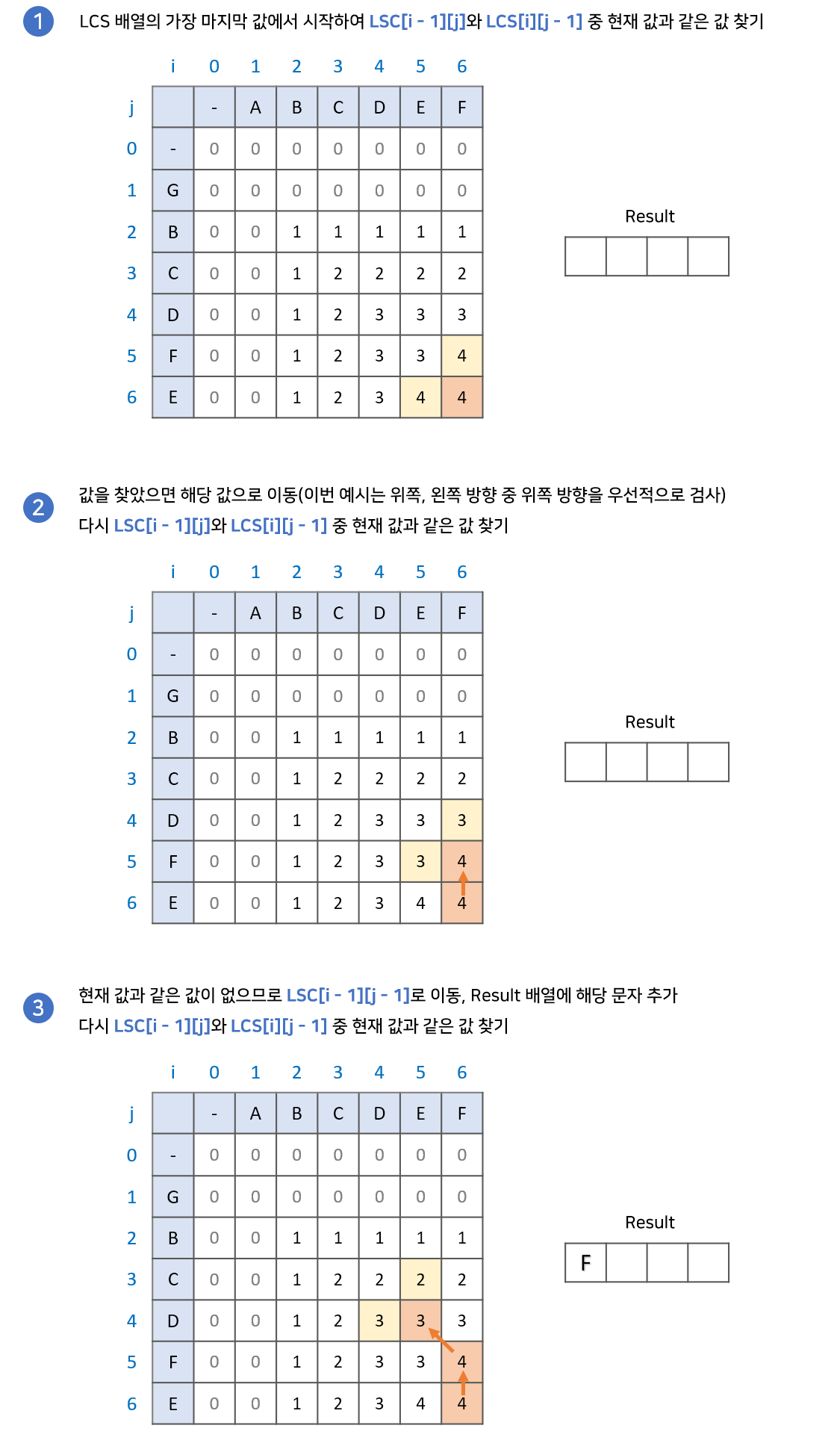
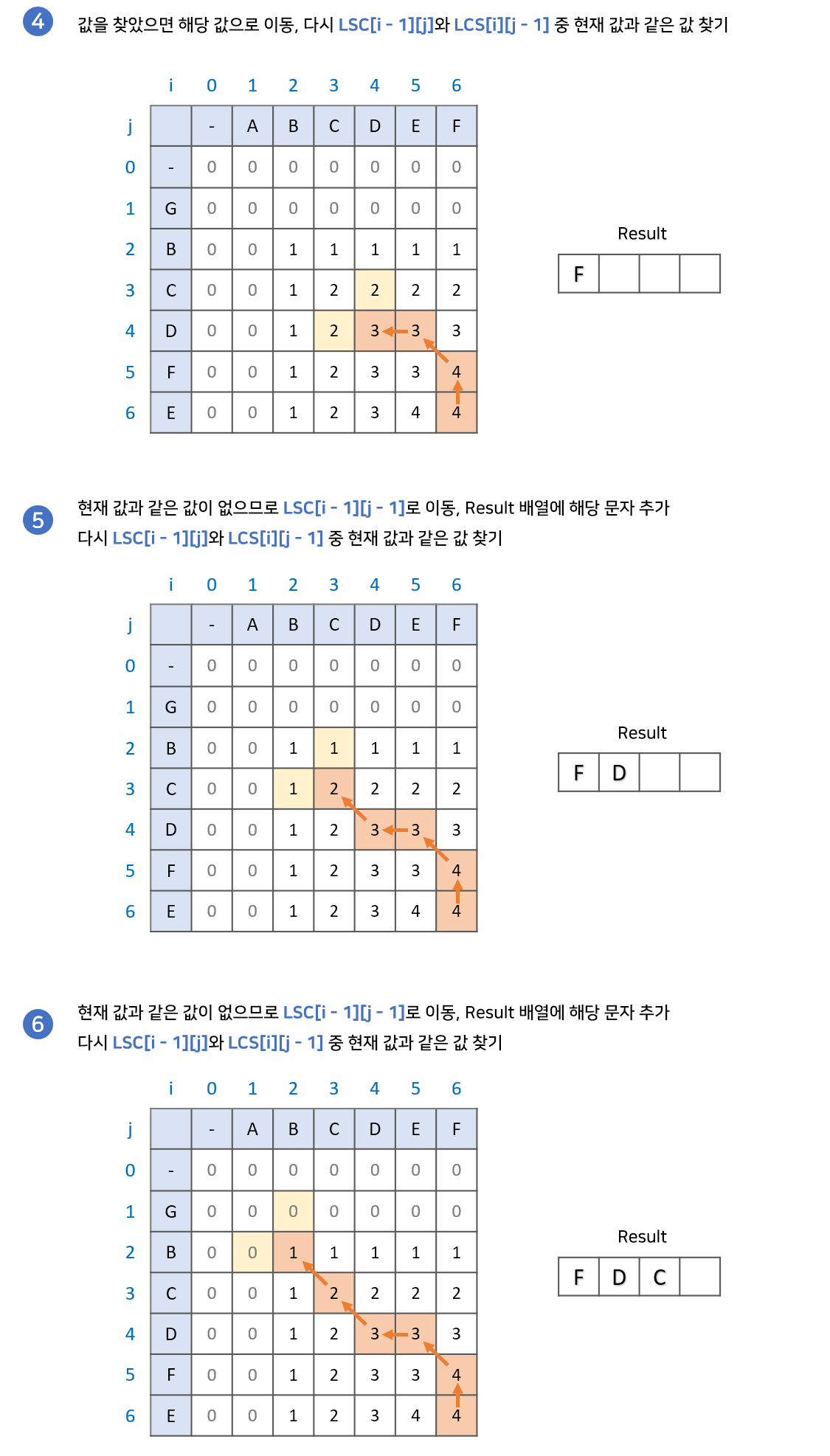
마치며
최장 공통 부분수열(Longest Common Subsequence)과 최장 공통 문자열(Longest Common Substring)에 대해 포스팅 해보았습니다. 이후 포스팅 역시 DP에 자주 활용되는 알고리즘을 포스팅 하겠습니다.
20개의 댓글
정말 좋은 포스팅 감사합니다.
A, B, C, D, E, F 와 G,B,C,D,F,E,Z,K 를 이용하여 비교해봤을때
result 배열을 생성을 하기 위해 탐색 우선순위를 왼쪽부터 하는 것과 위쪽부터 하는 것이 그 결과가 사뭇다르던데요.
이거는 그냥 무시하는 현상일까요?
아니면 왼쪽이나 위쪽에 대해 우선순위를 두는 조건이 따로 있는 걸가요?

















good!!