[CS] 소스코드에서 소숫점 계산시 오차가 발생하는 이유?

David Im·2022년 8월 23일

예전에 데이터에 대한 계산을 진행하다가 나는 4.9에 대한 전체 값의 합의 평균을 구했는데 결과값이 딱 떨어지지 않고 .999999999와 같이 무한 소수로 내려가는 현상을 발견한 적이 있었다.

그래서 round() 함수를 통해서 반올림하는 방식을 사용해서 해결했었는데, 정확한 원인에 대해서 왜 그랬는지 그때는 제대로 이해하지 못했다가 이번에 이직준비를 하면서 알고리즘과 CS공부를 진행하면서 제대로 알게 되었다.

컴퓨터의 2진 체계

우리가 아는 컴퓨터는 2진 체계인 0과 1로 구성하여 데이터를 처리한다.

정수의 저장 체계

이진 체계를 사용하는 컴퓨터는 우리가 2를 입력하면 0010으로 저장하고 5라는 이진체계로 나누어떨어지지 않는 숫자는 0101로 저장한다. 10909을 입력하면 10101010011101와 같이 긴 숫자로 변형되어 저장한다.

즉 뒤에서부터 1, 2, 4, 8, 16 ... 이런식으로 계산하면서 올라가게 되는 것이다.

소수의 저장 체계

그렇다면 소수의 저장은 어떻게 하게 될까?
5.125 라는 숫자를 예로 들어보겠다.

이 숫자는 2진수로 변하게 될 경우 101.001로 치환된다.

이 숫자를 저장하려면 어떻게 컴퓨터에서 처리할까?

단순히 생각해보면 위의 값처럼 101.001로 정수부분과 소수부분으로 나누어서 저장을 하겠지만 우리는 이 숫자를 가지고 연산도 하고 프로그래밍적 처리를 한다고 하면 다른 방식을 사용해야한다.

컴퓨터의 소수 저장 방법

우리가 흔히쓰는 이 소수를 쓸때 float 형식에 저장을 하게 된다. 이 float가 어떻게 저장을 하는지 알아보자.

공간확보
메모리 공간을 우선적으로 확보하여 32자리 정도를 확보한다.
맨 첫번째는 우선 부호비트 자리이다.
양수이면 0, 음수이면 1을 저장한다.

5.125라는 숫자를 2진수로 변환한다.
해당 숫자를 2진수로 변환하면 101.001이었는데 해당 숫자에서 소숫점을 맨 앞으로 땡겨와서 1.01001로 치환하고 2진수인 $2^2$ 를 곱해준다.
➡️ 1.01001 x $2^2$ 라는 숫자로 치환된다.

이떄 소숫점 뒤에 숫자인 01001 부분은 mantissa라고 하여 상용 로그값의 소수부분을 의미하는데 이 값을 32자리 중에서 뒤에서부터 23자리까지 순서대로 채워넣는다

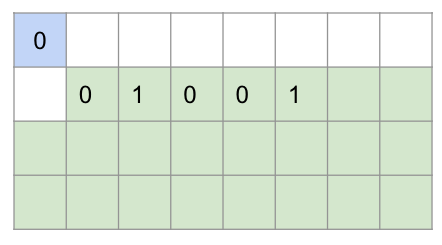
정수 부분 채우기
부호비트와 소수부분을 제외한 사이의 남은 8자리에 대해 $2^2$ 중 지수부분에 127을 더해서 2진수로 변환하여 채워넣는다.

2 + 127 -> 10000001

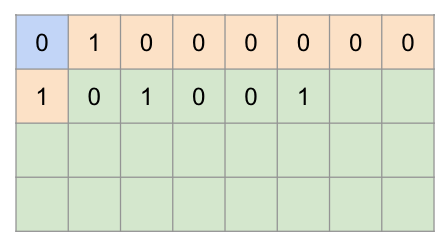
무한 소수는 어떻게?

위와같이 2진수로 딱 떨어지는 숫자들의 경우에는 저런식으로 저장이 가능하다. 그렇다면 0.1과 같은 무한 소수는 어떻게 저장을 할까? 위에서 문제가 되었던 .999999...와 같은 형태가 바로 이곳에서 발생하는 것이었다.

실제로 0.1이라는 소수는 2진수로 변환하게 되면 0.0001100110011001100...과 같이 무한이 순회하는 무한소수가 된다. 우리가 할당한 32개의 비트로 채워넣기에는 공간이 부족하다.

이럴때 컴퓨터는 32개 자리를 벗어나는 뒤의 숫자들은 모두 잘라내고 32자리에 맞춰서만 저장한다.

그 뒷부분을 잘라내는 부분에서 발생하는 오차로 인해 특정값을 계산하게 되면 내가 겪었던 문제가 발생하는 것이다.

우리는 눈으로 1.1 + 0.1 은 1.2라는것을 알고있지만 컴퓨터의 저장방식에서는 해당하는 값은 1.2가 아닌것이 되는 셈.

그래서 아래와 같은 코드로 확인해보면 실제로 리턴값이 false가 반환되는것을 확인 할 수 있다.

def is_sum_true(input1, input2):
	input1 = 0.1
	input2 = 1.1
    
	if a + b == 1.2
    	return True
	else:
    	return False

> False

그럼 우리는 어떻게 이 문제를 해결하는가?

정확한 계산이 필요한 부분은 정수로 계산하자
우리는 글로벌 서비스를 하였기때문에 판매하는 상품이 달러화로 표기를 했었다. 그렇기 때문에 4.99달러, 10.99달러와 같이 표기하였는데 실제로 계산시에도 이 값을 float형식으로 그대로 사용하다 보니 문제가 발생했었던 것이었기에 round()로 소숫점을 전부 올려서 정수형태를 만들어 주었더니 해결된 게 이 케이스다.

만약 위에와 같이 정확한 계산이 필요한 값이라면 계산이 필요한 값을 완전히 정수로 변환하여 사용하도록하자.

4.99달러 ➡️ 4990센트

float a = 4.99 ➡️ X
int a = 4990 ➡️ O
반올림 문법을 사용하자
굳이 float를 사용해야하는 상황이라면 내가 해결했던 방법처럼 계산할때는 반올림을 하여 정수형으로 변환해 사용하는것도 방법이다.

python의 round에서는 사사오입 원칙을 적용하기때문에 내가 사용한 4.99달러의 경우에는 5달러가 되어 0.01의 오차가 생기긴 한다.

a = 4.99
b = round(a)
➡️ b = 5

double 자료형을 사용하자
정말로 소숫점 계산이 필요하다면 이것도 방법일 수 있다.

double자료형은 기존에 32자리까지 표기가능했던 float형식에서 2배로 늘려 숫자 1개당 64자리까지 지원이 가능하도록 하는 형식이다.
이 방식을 사용하면 우리가 사용하는 일반적인 소수정도들은 거의 커버가 가능하겠지만 단점으로는 메모리를 2배로 잡아먹는다는 것이 단점인지라, 메모리 관리가 필요한 데이터가 로직일 경우에 사용하려면 조금 고려해야 할 필요가 있다.

마무리

참 기본적인 내용이고, 컴퓨터공학 시간에 배웠던 내용인데도 실무에 치이다보니 이런 기초적인 내용을 잊어버리고 살았던게 스스로 부끄럽기도 했다. 이직 준비하면서 CS공부도 하고 알고리즘 공부도 하다보니, 그동안 내가 짰던 코드에서 발생하는 원리부터 해결하지 못했던 부분에 대한 이해까지 하나 둘씩 풀려가는 것을 느낄 때마다 CS지식은 정말 계속해서 익혀두어야겠다는 생각이 드는 시점이었다.

날 구해준 유튜브 알고리즘 땡큐!