어텐션 시커

❗️이 글은 위키독스로 공부하고 정리한 글임❗️

✴️Attention

Attention의 등장

seq2seq은 시퀀스 정보 처리에 탁월하지만, 다음과 같은 한계가 있었다:
1. 컨텍스트 벡터에 모든 정보를 압축하니 정보 손실이 생기고,
2. 기울기 소실 문제 발생한다.

이로 인해 입력 시퀀스가 길어지면 떨어지는 출력 시퀀스의 정확도를 보정하는 Attention 이 등장한다.
어텐션은 매 시점마다 전체 입력 문장 중 연관 있는 입력 단어 부분을 다시 참고하여, 위 언급한 문제를 해결할 수 있었다.

Attention 메커니즘

어텐션을 이해하려면 Key, Value, Query의 개념을 이해해야 한다.
Key와 Value는 {Key: Value} 이런 형태를 갖는다. 가령 {"2017" : "Transformer", "2018" : “BERT"} 에서 key는 2017과 2018, value는 Transformer과 BERT가 되는 것!

어텐션에서의 K, V, Q는 이런 구조를 가진다.

어텐션에서 각 값이 가지는 의미는 이렇다:
Q = Query : t 시점의 디코더 셀에서의 은닉 상태
K = Keys : 모든 시점의 인코더 셀의 은닉 상태들
V = Values : 모든 시점의 인코더 셀의 은닉 상태들

주어진 쿼리에 대해 모든 키와의 유사도를 구하고, 그렇게 구한 유사도를 각각의 밸류에 반영한다. 유사도가 반영된 밸류를 모두 더해서 리턴하면
어텐션 값 (Attention Value) 이 된다.

이 어텐션 값은 출력 단어 예측에 필요한 중요한 값이다.

Dot-Product Attention

그렇다면 이젠 어텐션 값을 구해보자.

1. Attention Score

어텐션 메커니즘에서는 디코더 셀이 세 개의 입력값을 가진다.
이전 시점 t-1의 은닉 상태, t-1의 출력 단어, 그리고 $a_t$가 그것이다.
$a_t$는 t번째 단어를 예측하기 위한 어텐션 값이다. $a_t$를 구하기 위해서 어텐션 스코어가 필요하다.

어텐션 스코어는 현재 시점 t의 디코더에서 단어를 예측하기 위해 인코더의 모든 은닉 상태 각각이 디코더의 현 시점의 은닉 상태 $s_t$와 얼마나 유사한지 판단하는 값이다.

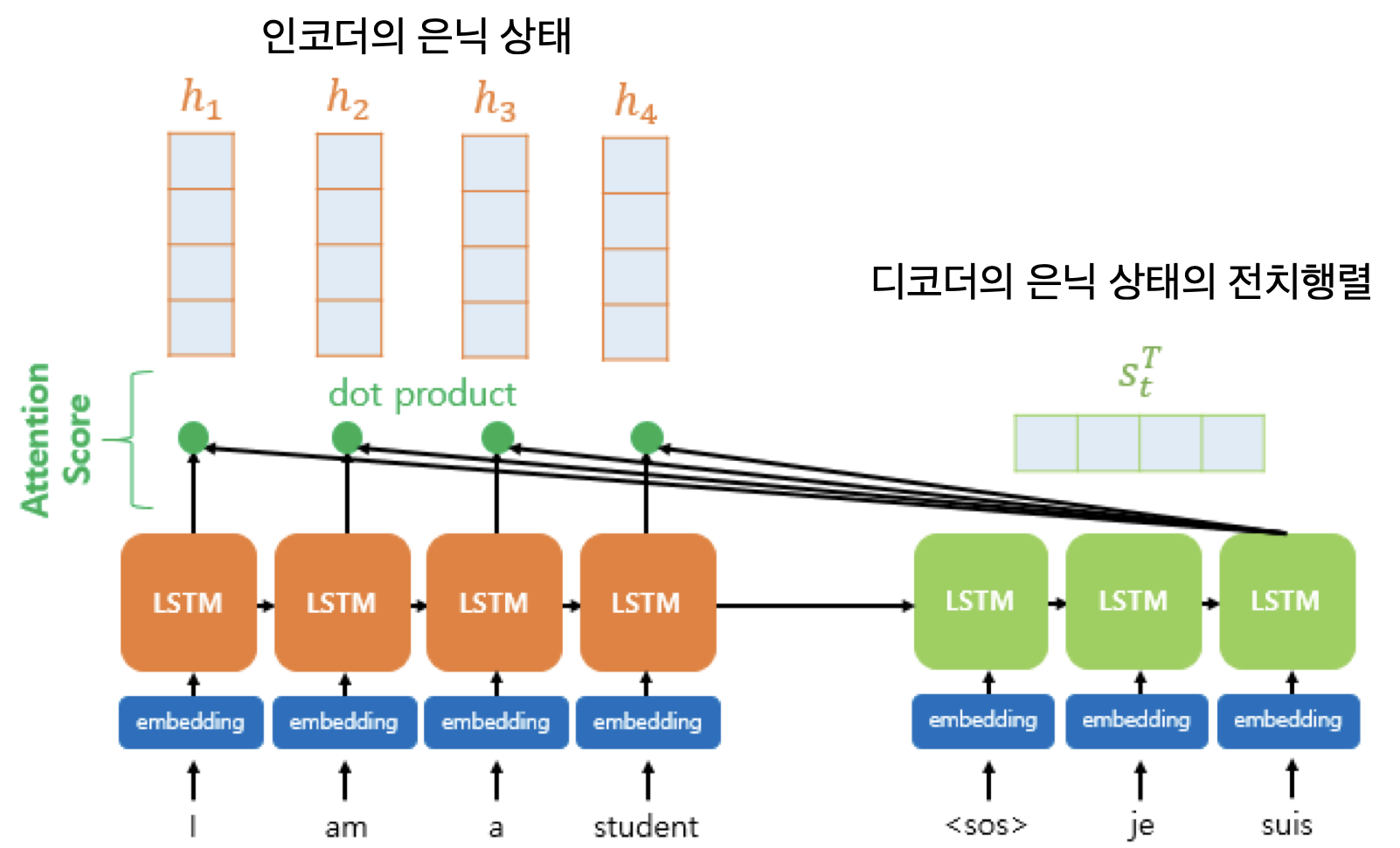
각 인코더 셀의 은닉 상태는 $h_i$, 디코더 셀의 은닉 상태는 $s_t$라고 했을 때,

$s_t$의 전치행렬과 $h_i$를 dot product하면 어텐션 스코어가 나온다.
$score(s_{t},\ h_{i}) = s_{t}^Th_{i}$

모든 은닉 상태의 어텐션을 모은 값은 $e^t$로 표현한다.
$e^{t}=[s_{t}^Th_{1},...,s_{t}^Th_{N}]$

2. Attention Distribution

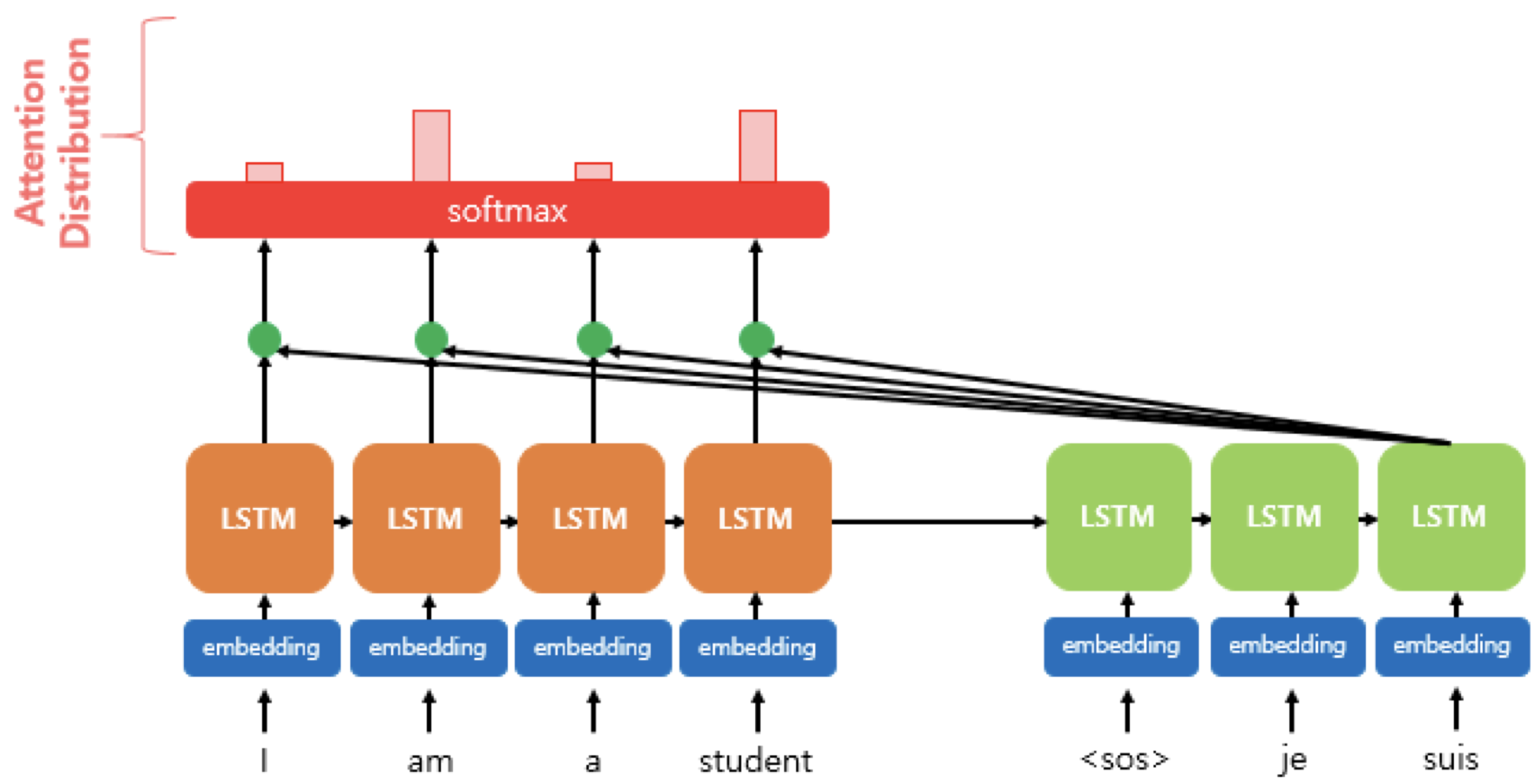
$e^t$에 소프트맥스 함수를 적용하면 모든 값을 합해 1이 되는 확률 분포를 얻게 되는데, 이를 어텐션 분포 라고 한다. 위 그림에서 빨간색 사각형은 각 셀의 어텐션 가중치를 나타내는 것으로, 클수록 해당 셀의 어텐션 가중치가 높다는 뜻이다.

디코더의 시점 t에서 어텐션 가중치의 모은값인 어텐션 분포는 $α^t$ 로 표기한다.
$α^{t} = softmax(e^{t})$

3. Attention Value 와 은닉 상태 연결

그렇다면 이제는 정말 어텐션 값을 구할 차례이다!

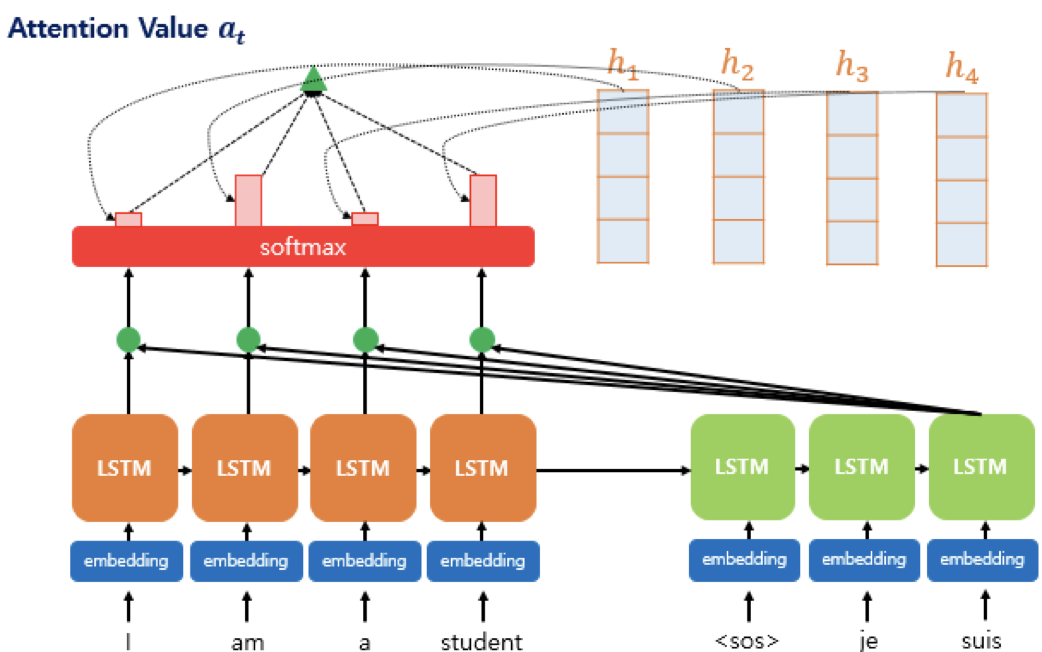
각 시점의 어텐션 가중치와 은닉 상태를 곱하고, 모든 시점에 대해 더하면 우리가 구하고자 했던 $a_t$ 가 나온다.

$a_{t}=\sum_{i=1}^{N} α_{i}^{t}h_{i}$

$a_t$ 는 인코더의 문맥을 포함하고 있기 때문에 컨텍스트 벡터 라고도 부르는데, seq2seq에서는 인코더의 마지막 은닉 상태를 컨텍스트 벡터라고 했다. 정보를 압축해서 가지고 있는건 똑같으니까 같은 맥락이라고 봐도 되겠다.

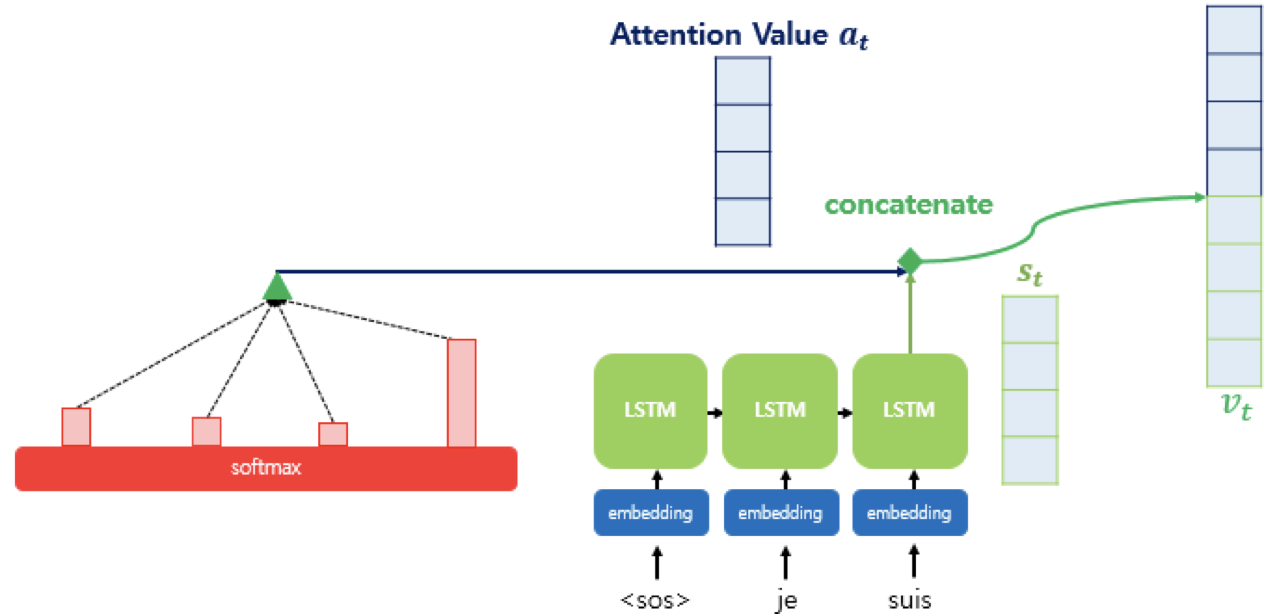
그 다음에는 $a_t$ 와 $s_t$ 를 결합해서 $v_t$ 라는 하나의 벡터를 만든다. 이 $v_t$ 는 $\hat{y}$, 그러니까 출력값의 입력으로 사용된다. 즉 인코더로부터 얻은 정보를 활용해서 출력 단어를 예측할 수 있게 되는 것이다!

4. 출력 벡터 계산

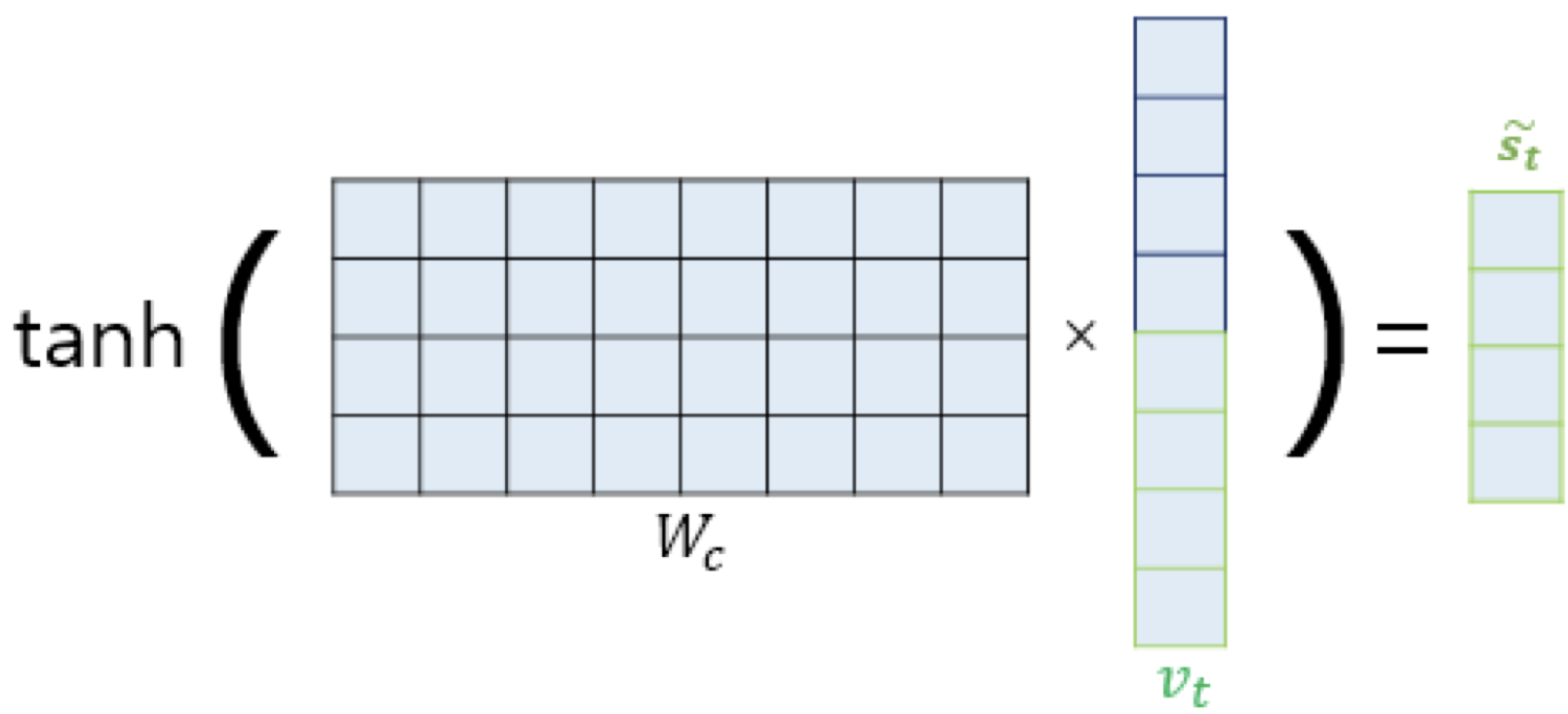
$v_t$를 바로 출력층으로 넣기 전에 어디서 나온건지 모르겠는 가중치 행렬 $W_c$ 와 곱한 다음 tanh 함수를 씌워서 새로운 벡터 $\tilde{{s}}_{t}$ 를 구한다.

$\tilde{s}_{t} = \tanh(\mathbf{W_{c}}[{a}_t;{s}_t] + b_{c})$

그 다음 $\tilde{s}_{t}$를 출력층의 입력으로 사용하여 예측 벡터를 얻는다.

$\widehat{y}_t = \text{Softmax}\left( W_y\tilde{s}_t + b_y \right)$

Badanau Attention

어텐션은 어텐션 스코어를 구하는 방법에 따라 달라진다.
지금까지 봤던 ‘Dot product’ attention, ‘scaled dot’, ‘concat’ 등등..
그 중 바다나우 어텐션은 concat 방법을 사용한 어텐션이다. 이름은 논문 저자인 Badanau에서 따왔다고. 참고로 dot-product 어텐션은 Luong 어텐션이라고도 한다.

• Luong
  $score(s_{t},\ h_{i}) = s_{t}^Th_{i}$
• Badanau
  $score(s_{t-1},\ h_{i}) = W_{a}^{T}\ tanh(W_{b}s_{t-1}+W_{c}h_{i})$

스코어 함수를 비교해보면 확연히 차이점을 알 수 있다.

바다나우의 특징은 Query가 t-1 시점의 은닉 상태라는 것이다. t 시점이었던 루옹과 구별되는 부분이다.

Q = Query : t-1 시점의 디코더 셀에서의 은닉 상태
K = Keys : 모든 시점의 인코더 셀의 은닉 상태들
V = Values : 모든 시점의 인코더 셀의 은닉 상태들

이제 바다나우의 메커니즘을 살펴보자.

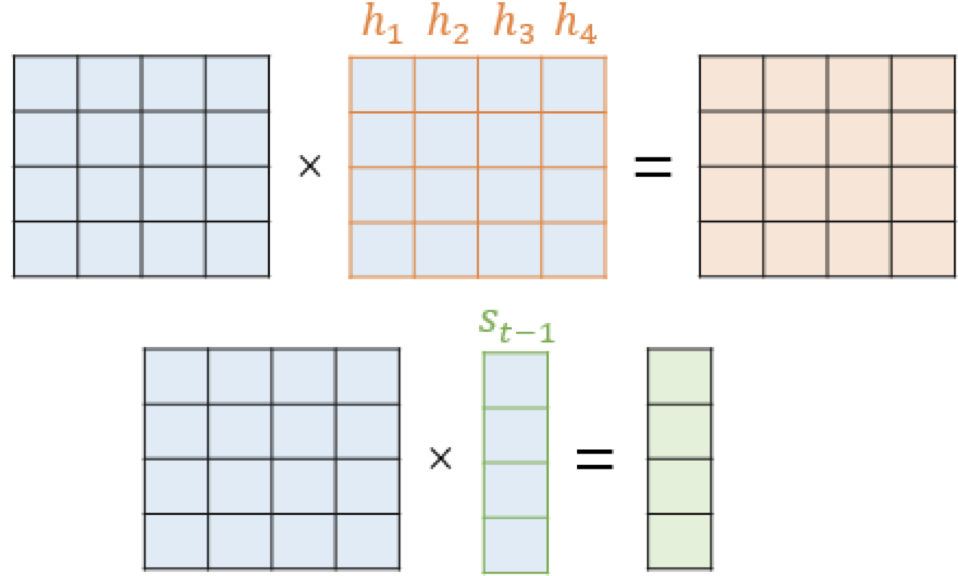
$W_{b}s_{t-1}$와 $W_{c}H$를 더한다. H는 인코더의 은닉 상태인 $h_i$ 를 하나의 행렬로 모은 것이다.$W_a, W_b, W_c$ 는 모두 학습 가능한 가중치 행렬이라고 한다. 몬소린지 모르겠

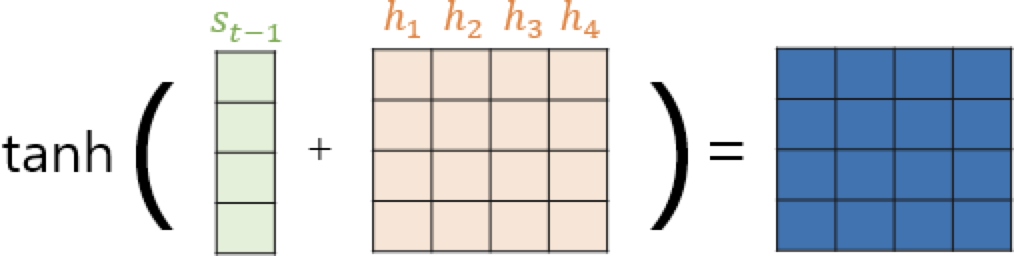
$W_{b}s_{t-1}$ 와 $W_{c}H$ 에 tanh함수를 입힌다.

이렇게 되면 어텐션 스코어가 나온다.
$e^t = W_{a}^{T}\ tanh(W_{b}s_{t-1}+W_{c}H)$

그 다음은 내적 어텐션이랑 같다. 소프트맥스 함수 씌워서 어텐션 분포 구하고, 인코더의 은닉 상태와 어텐션 가중치 곱해서 컨텍스트 벡터(=어텐션 값)를 구한다.

아이고 복잡하다! 다음에는 논문도 꼭 읽어봐야지.

어떻게 마무리하지...