[자료구조] 정렬

김서연·2025년 8월 12일

자료구조와 알고리즘

목록 보기

3/4

정렬 알고리즘과 시간복잡도

정렬은 자료를 크기 순서대로 배열하는 알고리즘이다. 비교와 이동을 통해 정렬하기 때문에, 최대한 효율적으로 알고리즘을 짜는게 관건이다. 그리고 이 효율성은 시간복잡도를 기준으로 판단한다. (공간복잡도도 있긴 하지만 암튼)

시간복잡도를 표현할 때는 Big O 표기법을 사용한다.

알고리즘이 n개의 자료를 처리할 때 소요되는 시간을 대략적으로 가늠해서 최고차항만을 처리시간으로 간주한다.

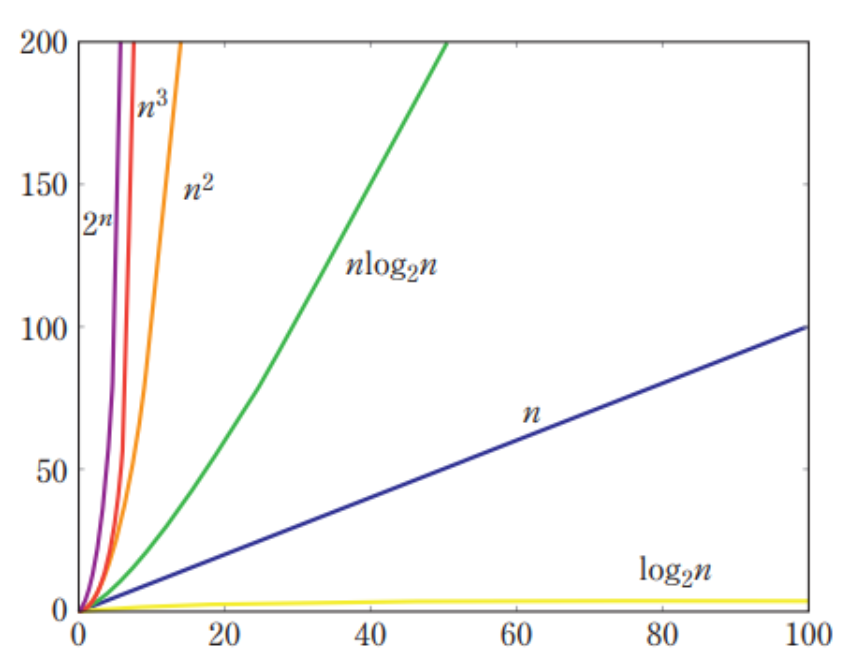
시간	이름	특징	N이 1000일 때 연산 횟수
$O(1)$	상수 시간	입력 크기(n)와 상관없이 일정한 연산 횟수로 진행	1
$O(logn)$	로그 시간	입력 크기에 따라 연산 횟수가 로스 함수를 따라 증가. 이진탐색	10
$O(n)$	선형 시간	입력 크기와 선형적으로 비례.	1000
$O(nlogn)$	선형로그 시간	입력을 반으로 줄여서 작업을 수행. 퀵정렬	10000
$O(n^2)$	이차 시간	입력 크기의 제곱만큼 연산을 수행. 선택정렬, 삽입정렬	1000000
$O(n^3)$	삼차 시간		1000000000
$O(2^n)$	지수 시간		1.1e+301

일반적인 코테에서는 $O(n^3)$ 을 넘어가면 사용하기 어렵다고 한다. 연산횟수가 10억을 넘어가면 C언어 기준 1초 이상의 시간이 소요되는데, N의 크기가 5000을 넘는다면 10초 이상 걸릴 수 있다. 문제의 조건을 보고 N 범위에 따라 얼마나 효율적인 알고리즘을 작성해야 하는지 힌트를 얻을 수도 있다.

시간제한이 1초인 문제에 대해 다음 시간 복잡도 이하면 문제를 풀 수 있다.

N <= 500: $O(n^3)$
N <= 2000: $O(n^2)$
N <= 100000: $O(nlogn)$
N <= 10000000: $O(n)$

선택 정렬

정렬되지 않은 리스트에서 가장 작은 값을 선택하여 이 값을 정렬된 리스트의 끝으로 옮긴다.

가장 작은 값의 처음 시작은 정렬할 자리에 원래 있던 원소이다. 옆에 있는 원소와 비교했을 때 더 작으면 가장 작은 값이 업데이트가 되고, 이어서 옆으로 하나씩 넘어가면서 비교해서 정렬해가는 식이다.

두 개의 중첩된 반복문을 사용하기 때문에 $O(n^2)$ 의 시간복잡도를 가진다. 그다지 효율적이진 않다.

구체적인 순서는 다음과 같다.
1. 정렬해야 하는 자리 i가 있다. 이게 최초의 least 값이다. 이를 Aj와 비교한다. 우리의 목적은 least를 찾아서 업데이트시키고, 최종적으로 이 least값을 i 자리에 배치하는 것이다.
2. 만약 A[j]가 더 작다면 least=j로 업데이트한다. 이걸 j가 리스트 끝까지 갈 때까지 반복해서 least를 찾는다.
3. A[least]가 i 자리에 와야 하기 때문에 둘을 바꾼다. 이때 둘을 바꾸는 이유는 A[i]는 아직 정렬이 되지 않았기 때문에 뒤로 보내서 정렬 후보로 남겨야 하기 때문이다.
4. 이걸 계속 반복한다.

코드

def selection_sort(A):
	n = len(A)
    for i in range(n-1):
    	least = i
    	for j in range(i+1, n):
        	if (A[i] < A[least]:
            	least = j
        A[i], A[least] = A[least], A[i]

예시

초기 리스트: [6, 5, 10, 12, 1, 2, 4, 19]
1. i=0부터 정렬한다고 했을 때 최초 least=0이다.
2. j=1: 6과 5(j=1)를 비교한다. 이때 5<6이기 때문에 least=1이 된다.
3. j=2: A[j]=10, A[least]=5 이므로 least는 업데이트되지 않고 그대로 1이다. j=3일 때도 마찬가지.
4. j=4: A[j]=1, A[least]=5 이므로 least=4가 된다.
5. 계속 비교를 해도 1(=A[least])보다 작은 값이 없으므로 최종적으로 i=0 자리에는 1이 와야한다. 즉 A[i]와 A[least]의 위치를 바꿔준다. 덮어쓰기 하면 6이 사라지므로 교환한다.
6. 지금까지 정렬된 현황은 [1, 5, 10, 12, 6, 2, 4, 19]이다. 그다음 i=1로 넘어가므로 5와 이후 남겨진 원소들을 비교해서 또 정렬한다.
7. ...

삽입 정렬

정렬할 값을 순서에 맞는 위치에 삽입하는 과정을 반복한다.

첫번째 원소는 그대로 있고 두번째 원소부터 첫번째와 비교한다. 만약 두번째가 더 작다면 첫번째 앞에 끼워넣는다. 그 다음 세번째 원소를 첫번째, 두번째 원소와 비교해서 또 제자리에 삽입하는 식이다. 이때 정렬할 대상을 미리 다른 변수에 저장해두어야 덮어쓰기가 되지 않는다.

더 작은 값을 만나면 비교를 멈추고 그 자리에 삽입하기 때문에 정렬되지 않은 리스트 전부를 비교해야 하는 선택정렬보다 비교과정이 적어진다.

제대로 이해한게 맞을진 모르겠지만 스스로 생각했을 때 선택정렬과 삽입정렬은 정렬하는 순서가 반대같다.
선택정렬은 정렬 리스트에 정렬된 원소들을 뒤쪽으로 붙여나가고, 이렇게 정렬된 리스트는 바뀌지 않는다. 반면 삽입정렬은 앞쪽으로 비교해서 정렬을 해나간다. 즉 앞쪽에 정렬된 리스트가 최종이 아니고, 사이사이 삽입하면서 점차 정렬되는 것이다.

코드

def insertion_sort(A):          #삽입 정렬 함수
    n = len(A)                  #입력 리스트의 크기(길이)를 구한다.
    for i in range(1, n):        
        temp = A[i]            #정렬 대상 값 
        j = i
        while j > 0 and A[j-1] > temp:  #앞쪽으로 비교해 나간다.
            A[j] = A[j-1]    #더 큰 값은 뒤쪽으로 이동시킨다.
            j -= 1
        A[j] = temp

예시

초기 리스트: [6, 5, 10, 12, 1, 2, 4, 19]
1. i=1: 현재 temp=5, A[j-1]=6이다. 6>5이므로 더 큰 값을 뒤쪽, 그러니까 i=1에 이동시킨다. j-=1 하면 j=0이 되므로 A[0]=5가 되고 다음 i로 넘어간다. 현재 리스트는 [5, 6, 10, 12, 1, 2, 4, 19]
2. i=2: temp=10, A[2-1]=6. 6 < 10이므로 패스. A[0]=5 < 10이므로 여기서 끝.
3. i=3: 마찬가지.
4. i=4: temp=1, j=4, A[4-1]=12. 12>1이므로 A[4] 자리에는 12가 들어감.
4-2. 그다음 j=3 역시 A[2]=10>1이므로 A[3] 자리에는 10이 들어감.
...
j=1일 때 A[0]=5>1이므로 A[1]자리에는 5가 들어가고 j=0 되어서 while 루프 끝나서 A[0]는 1이 됨. 현재까지 리스트 [1, 5, 6, 10, 12, 2, 4, 19]

퀵 정렬

퀵정렬은 이름 그대로 "빠르다". 위 두 방법보다 빠르다고 한다. 분할 정복 알고리즘(divide-and-conquer)에 기반하여 정렬하는 방법이다.
퀵정렬은 크게 세가지 동작으로 이루어진다.

[분할] 기준이 되는 피벗이라는 원소를 선택한 후, 피벗보다 작은 원소는 피벗의 왼쪽으로, 피벗보다 큰 원소는 오른쪽으로 이동시킨다. 이러면 리스트가 피벗을 기준으로 두 리스트로 분할이 된다.
[정복] 분할이 된 두 리스트를 또 정렬한다.
[결합] 정렬이 끝난 부분 리스트를 결합하여 최종적으로 정렬된 리스트를 반환한다.