백준 1041번 주사위

🔒문제 url

https://www.acmicpc.net/problem/1041

🔑알고리즘

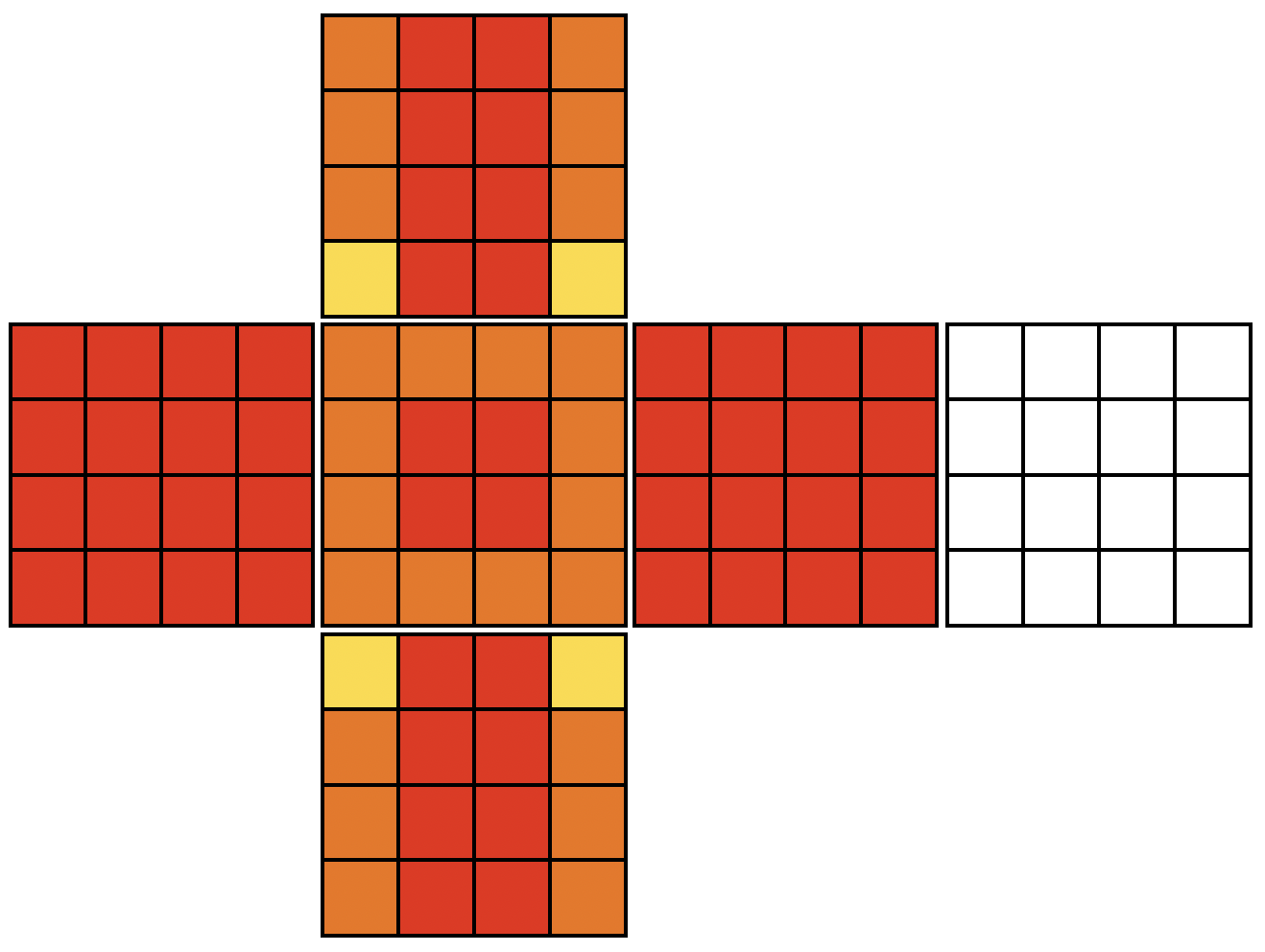
주사위를 구성하는 숫자 중 3개를 택해 오름차순 정렬한 것을
빨강색($X$), 주황색($Y$), 노랑색($Z$)으로 나타냈을 때, 합이 최소가 되는 상태는 아래와 같다.
$n = 4$일 때의 예시이다.

• 빨강색($X$) 영역
  • 전부 빨강색인 영역 : $2n^2 \times X$
  • 테두리를 제외하고 빨강색인 영역 : $(n-2)^2 \times X$
  • 양 끝 줄을 제외하고 빨강색인 영역 : $2n(n-2) \times X$
  • 합 : $(5n^2 - 8n + 4) \times X$
• 주황색($Y$) 영역
  • 테두리가 주황색인 영역 : $(n^2-(n-2)^2)\times Y$
  • 나머지 주황색 영역 : $4(n-1) \times Y$
  • 합 : $(8n-8)\times Y$
• 노랑색($Z$) 영역
  • 합 : $4\times Z$
    
    
• 총 합 : $(5n^2 - 8n + 4) \times X + (8n-8)\times Y + 4\times Z$

---

가능한 모든 3개의 조합에 대해 위 식을 적용하여 최솟값을 출력한다.

• 이때, 하나의 주사위에 있는 두 개의 면이 모두 보일 수 없는 경우가 있다.
  따라서 이 경우는 제외하여 적용한다.
  • $A$와 $F$가 같이 속한 조합은 제외한다.
  • $B$와 $E$가 같이 속한 조합은 제외한다.
  • $C$와 $D$가 같이 속한 조합은 제외한다.

🐾부분 코드

void setAns()
{
    ans = min(ans,((5 * n * n - 8 * n + 4) * v[comb[0]]
             + (8 * n - 8) * v[comb[1]]
             + 4 * v[comb[2]]));
}

<식 적용 및 최솟값 갱신>
구성된 세 개의 조합에 식을 적용하여 최솟값을 갱신한다.

void setComb(int depth)
{
    if(n == 1)
    {
        ans = accumulate(v.begin(), v.end(), 0)
              - *max_element(v.begin(), v.end());
        return;
    }
    if(depth == 3)
    {
        if(visited[0] && visited[5]) return;
        if(visited[1] && visited[4]) return;
        if(visited[2] && visited[3]) return;
        setAns();
        return;
    }

    for(int i = 0; i < 6; i++)
    {
        if(visited[i]) continue;

        visited[i] = true;
        comb.push_back(i);
        setComb(depth+1);
        visited[i] = false;
        comb.pop_back();
    }
}

<BackTracking으로 조합 구성>
$n = 1$인 경우는 식이 적용되지 않으므로 6면의 숫자의 합에서 최댓값을 뺀 값이 답이 된다.
accumulate()는 #include <numeric> 헤더를 통해 사용 가능하다.
위에서 언급한 조건을 만족할 때, 식을 적용하여 답안을 갱신한다.

🪄전체 코드

#include <iostream>
#include <vector>
#include <algorithm>
#include <numeric>

using namespace std;
#define IAMFAST ios_base::sync_with_stdio(false);cin.tie(0);

typedef long long ll;
ll n;
vector<ll> v(6);
vector<int> comb;
bool visited[6];
ll ans = 2e18;

void INPUT()
{
    IAMFAST
    cin >> n;
    for (int i = 0; i < 6; i++) cin >> v[i];
}

void setAns()
{
    ans = min(ans,((5 * n * n - 8 * n + 4) * v[comb[0]]
             + (8 * n - 8) * v[comb[1]]
             + 4 * v[comb[2]]));
}

void setComb(int depth)
{
    if(n == 1)
    {
        ans = accumulate(v.begin(), v.end(), 0)
              - *max_element(v.begin(), v.end());
        return;
    }
    if(depth == 3)
    {
        if(visited[0] && visited[5]) return;
        if(visited[1] && visited[4]) return;
        if(visited[2] && visited[3]) return;
        setAns();
        return;
    }

    for(int i = 0; i < 6; i++)
    {
        if(visited[i]) continue;

        visited[i] = true;
        comb.push_back(i);
        setComb(depth+1);
        visited[i] = false;
        comb.pop_back();
    }
}

void SOLVE()
{
    setComb(0);
    cout << ans;
}

int main()
{
    INPUT();
    SOLVE();
}

🥇문제 후기

가장 자신없는 Greedy 유형이었다. 그래도 골드 하위 문제는 어렵지않게 풀어서 다행이라며 위안삼았다..🤣🤣