백준 10836번 여왕벌

🔒[문제 url]

https://www.acmicpc.net/problem/10836

🔑알고리즘

1. 문제를 이해하자. 첫번째 열과 첫번째 행의 원소들은 왼쪽 아래에서부터 출발하여 윗 방향으로 간 후, 다시 오른쪽으로 가면서 성장의 크기는 오름차순이 된다.
2. 따라서, 첫 열과 첫 행을 제외한 지점의 성장 크기는 반드시 윗쪽 지점이 성장한 크기로 결정된다.
3. 초기 애벌레의 크기는 모두 1로 동일하므로, 첫 열을 제외한 하나의 열에 속한 애벌레는 매번 모두 같은 크기로 성장한다.
4. 즉, 매일 모든 지점의 애벌레를 갱신할 필요없이 첫 열과 첫 행의 애벌레의 최종 크기만 구한 후, 첫 열을 제외한 열은 모두 윗 행과 같은 수를 출력한다.

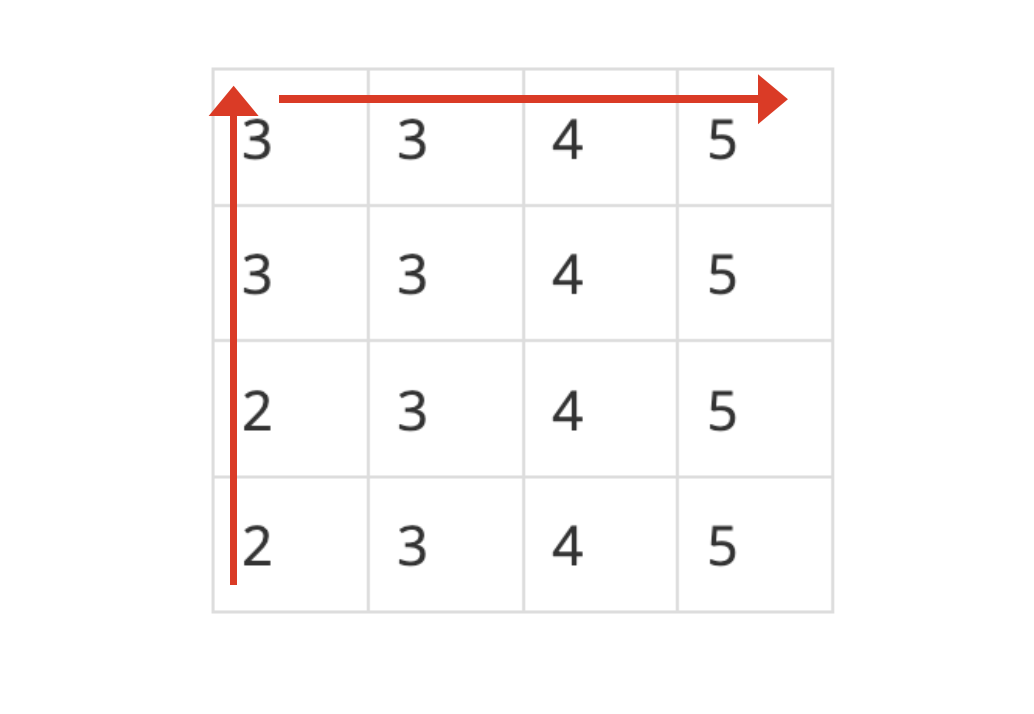
• 화살표 영역만 구한 후 나머지 영역은 윗 행과 똑같이 출력한다.
  

🐾부분 코드

void growFirst(int x,int y,int z)
{
    for(int i = 0; i < 2*m-1; i++)
    {
        if(x) x--;
        else if(y) map[i]++, y--;
        else map[i] += 2, z--;
    }
}

<첫 행, 첫 열 갱신 함수>
첫 행과 첫 열의 갯수는 총 $2m-1$개가 된다.
x y z는 각각 0의 갯수, 1의 갯수, 2의 갯수이다.

• 위에서 보인 사진에서의 화살표 방향으로 map[0] ~ map[2*m-2]에 원소를 담는다.
  map[0] ~ map[m-1] : 첫 열의 아래에서부터 원소를 담는다.
  map[m] ~ map[2*m-2] : 첫 행의 두번째 열부터 끝 열까지의 원소를 담는다.
• 이 함수를 $n$번 반복한다.

for(int i = 0; i < m; i++)
{
    cout << map[m-1-i] + 1 << " ";
    for(int j = m; j < 2*m-1; j++)
        cout << map[j] + 1 << " ";
    cout << '\n';
}

<답안 출력>
모든 애벌레는 1의 크기로 시작하므로, 0으로 초기화된 상태에서 최종 크기를 구했기때문에 1을 더하여 출력한다.
첫번째 열의 원소map[m-1-i] + 1를 먼저 출력한 후,
나머지 열의 원소map[j] + 1를 출력한다.

🪄전체 코드

#include <iostream>
#include <algorithm>
using namespace std;

int m,n;
int map[701+701];

void INPUT()
{
    ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    cin >> m >> n;
}

void growFirst(int x,int y,int z)
{
    for(int i = 0; i < 2*m-1; i++)
    {
        if(x) x--;
        else if(y) map[i]++, y--;
        else map[i] += 2, z--;
    }
}



void SOLVE()
{
    while(n--)
    {
        int a,b,c; cin >> a >> b >> c;
        growFirst(a,b,c);
    }

    for(int i = 0; i < m; i++)
    {
        cout << map[m-1-i] + 1 << " ";
        for(int j = m; j < 2*m-1; j++)
            cout << map[j] + 1 << " ";
        cout << '\n';
    }


}

int main()
{
    INPUT();
    SOLVE();
}

🥇문제 후기

모든 지점을 갱신할 경우, $O(n \times m^2)$의 시간 복잡도를 가지게 되어 시간 안에 통과하지 못 해 최적화의 단계를 거쳐야 하는 문제였다.
매우 퀄리티 높은 문제라고 생각한다. 추천추천!