🔒[문제 url]
https://www.acmicpc.net/problem/1167
🔑알고리즘
본 포스팅은 bedamino님의 그래프 증명을 참조하였습니다.
1. 임의의 정점 로부터 가장 먼 정점
2. 로부터 가장 먼 정점
- 와 의 거리가 트리의 지름이 된다.
- 위 명제에 대한 증명은 다음과 같다.
에서 가장 먼 노드를 , 와 의 거리를 트리의 지름이라고 하자.
그렇다면 다음과같은 경우를 갖는다.
- 인 경우 : 에서 가장 먼 가 가 되므로 참이다.
- 인 경우 : 1번과 동일하다.
- 인 경우 : 1번과 동일하다.
- 인 경우 : 1번과 동일하다.
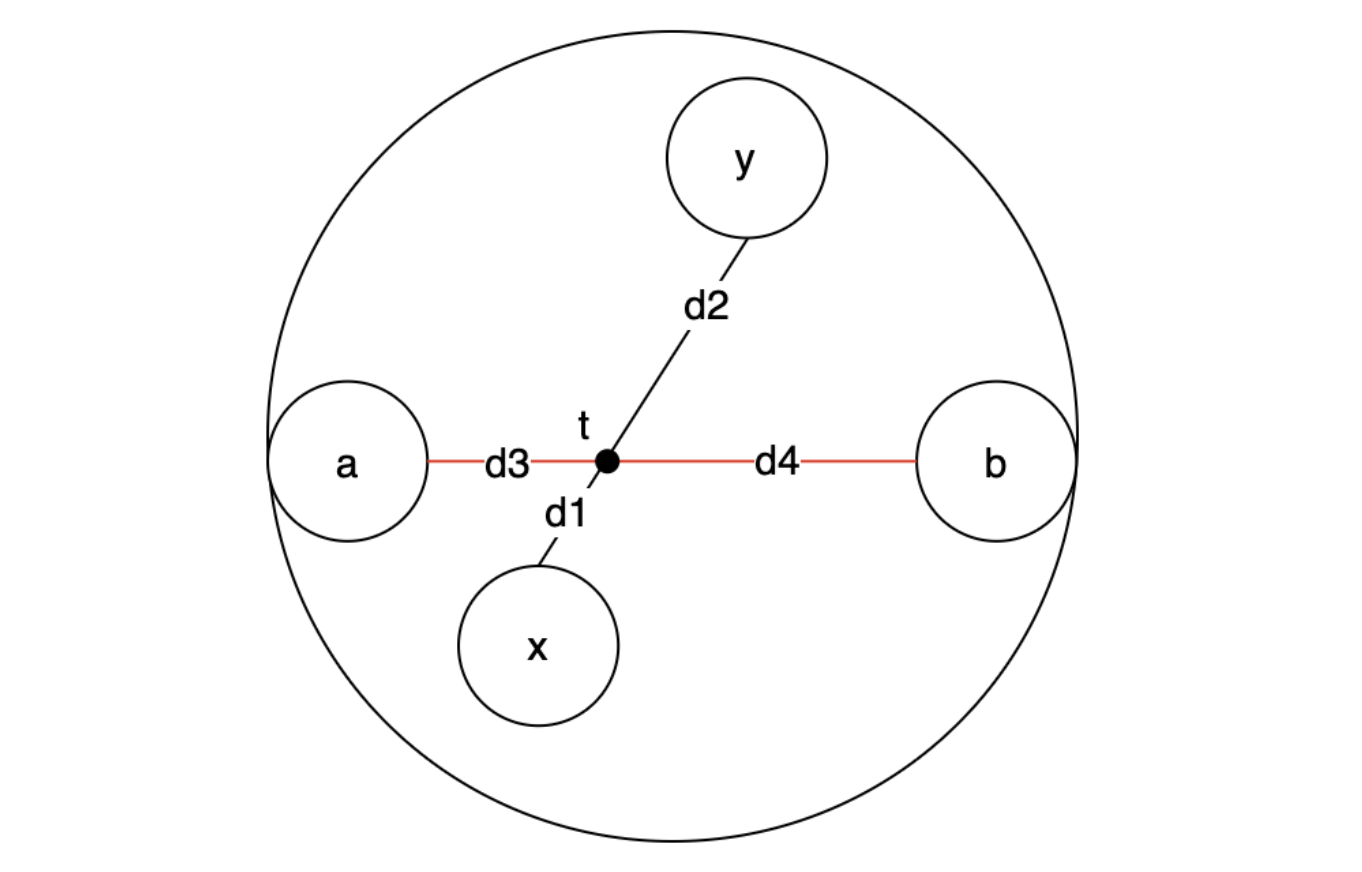
- 와 를 연결한 선분과, 와 를 연결한 선분이 교차하는 경우 :
에서 가장 먼 노드가 가 되기 위해서는,
의 길이가 가 되어야한다.
그렇게되면 3번 혹은 4번의 경우와 동일해지므로 참이다.
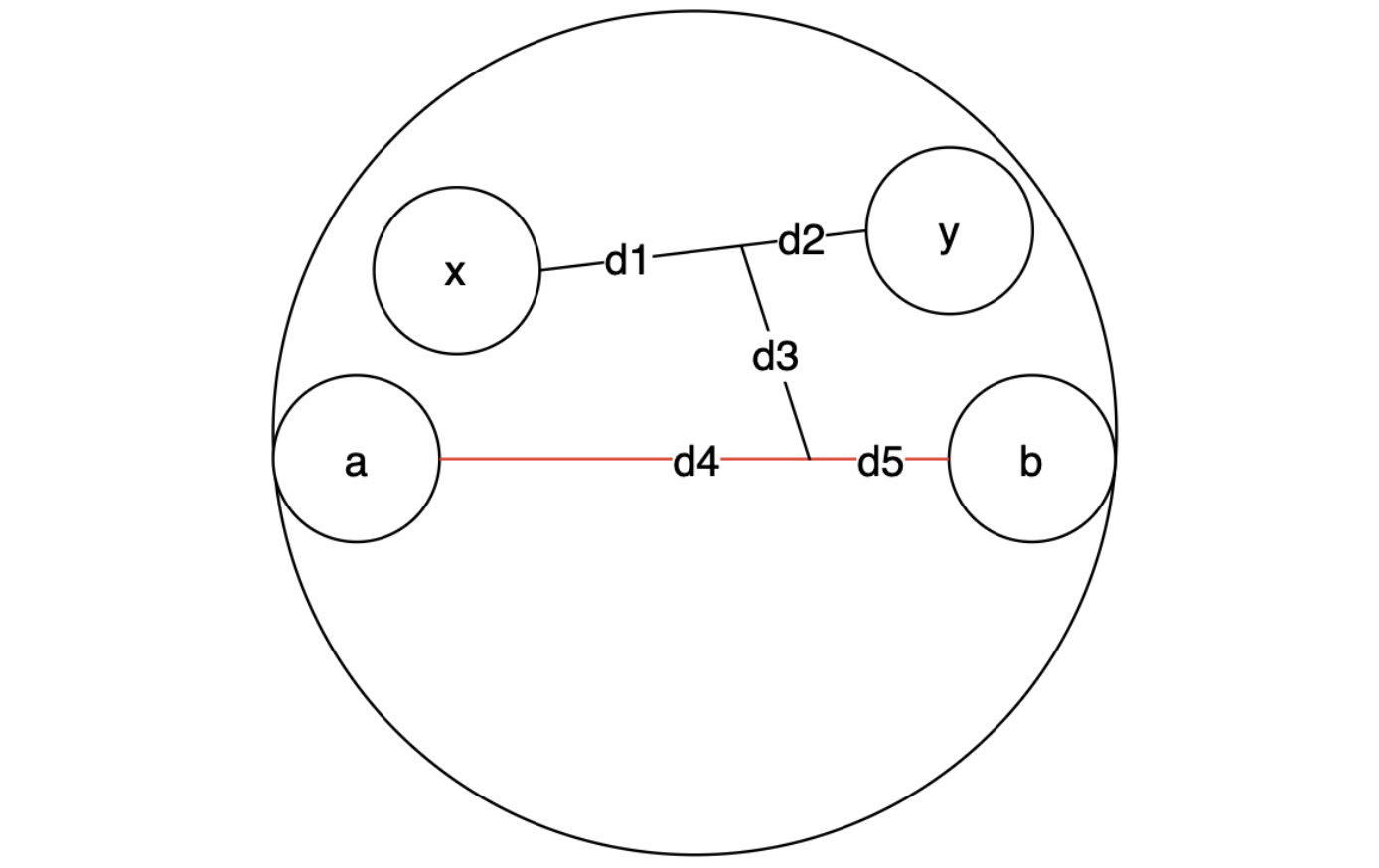
- 와 를 연결한 선분과, 와 를 연결한 선분이 교차하지 않는 경우 :
에서 가장 먼 노드가 가 되기 위해서는,
의 길이가 가 되어야한다.
그렇게되면 3번 혹은 4번의 경우와 동일해지므로 참이다.- 즉, 두 번의 DFS를 통해 답을 구할 수 있다.
🐾부분 코드
생략한다.
🪄전체 코드
#include <iostream>
#include <vector>
#include <algorithm>
#include <memory.h>
using namespace std;
#define IAMFAST ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);
int v;
int s,a,b;
typedef pair<int,int> pii;
vector<pii> graph[100001];
bool visited[100001];
int ans = -1;
void INPUT()
{
IAMFAST
cin >> v;
for(int i = 1; i <= v; i++)
{
cin >> s;
while(true)
{
cin >> a; if(a==-1) break;
cin >> b;
graph[s].push_back({a,b});
}
}
}
pii DFS(int x)
{//{가장 먼 노드의 번호 , 가장 먼 노드까지의 길이}를 반환한다.
int node = x;
int maxDist = 0;
visited[x] = true;
for(int i = 0; i < graph[x].size(); i++)
{
int nx = graph[x][i].first;
int dist = graph[x][i].second;
if(visited[nx]) continue;
pii temp = DFS(nx);
temp.second += dist;
if(maxDist < temp.second)
{
node = temp.first;
maxDist = temp.second;
}
}
visited[x] = false;
return {node,maxDist};
}
void SOLVE()
{
//가장 먼 노드의 번호를 가져온다.
int first = DFS(1).first;
//가져온 노드로부터 가장 먼 노드의 거리가 지름이 된다.
int second = DFS(first).second;
cout << second;
}
int main()
{
INPUT();
SOLVE();
}🥇문제 후기
무지성 DFS로는 이 나와 안 될걸 알았지만 방법을 떠올리지 못 해 끝내 아쉬움에 구현했다가 역시나 시초를 받고 블로그를 참조해 해결한 문제..🥲
내 두뇌가 매우 뛰어나지 않음을 인정하기 때문에, 그래프 이론을 포함한 많은 이론을 철저히 이해하고 많이 배우는 게 지름길 아닌 지름길이다.
💕오류 지적 및 피드백은 언제든 환영입니다. 복제시 출처 남겨주세요!💕
💕좋아요와 댓글은 큰 힘이 됩니다.💕
💕좋아요와 댓글은 큰 힘이 됩니다.💕