백준 1516번 게임 개발

🔒[문제 url]

https://www.acmicpc.net/problem/1516

🔑알고리즘

순서가 정해진 그래프? 위상정렬
반복되는 부분 문제를 통한 $n$번 건물을 짓기까지의 최소 시간? DP

• $dp_i$ : $i$번 건물을 짓기까지의 최소 시간
  - 위상정렬을 진행하며, 모든 건물에 대해 해당 건물 $i$을 짓기까지의 최소 시간을 저장한다.
  이때 최소 시간은 문제 조건에 따라
  해당 건물을 짓기 위해 지어야하는 건물 중 가장 오래 걸리는 건물을 짓기까지의 시간 + $Di$
  가 된다.
  
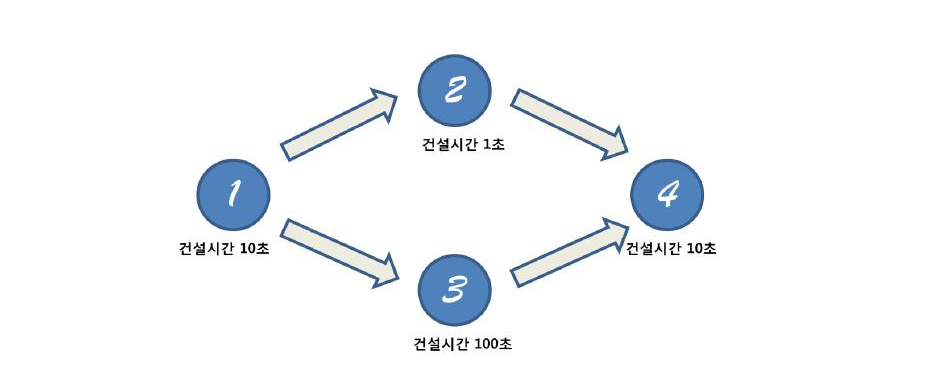
  1번 건물의 경우, 단독 건설이 가능하므로 $dp_1 = 10$
  2번 건물의 경우, 1번을 지어야하므로 $dp_2 = 10 + 1 = 11$
  3번 건물의 경우, 1번을 지어야하므로 $dp_3 = 10 + 100 = 110$
  4번 건물의 경우, 2번과 3번중 더 오래 걸리는 건물을 짓기까지의 시간에 4번 건물의 건설 시간을 더하므로 $dp_4 = 110 + 10 = 120$

🐾부분 코드

void INPUT()
{
    ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> Time[i];
        while (true)
        {
            int node; cin >> node;
            if (node == -1) break;
            graph[node].push_back(i);
            inDegree[i]++;
        }
    }
}

<입력 함수>
위상 정렬을 위해 각 노드에 대해 진입 차수 inDegree를 count한다.
문제 조건에 따라 -1 입력 시 $i$번 건물 정보의 입력을 종료한다.

void topology()
{
    queue<int> q;

    for (int i = 1; i <= n; i++)
    {
        if (inDegree[i] == 0) q.push(i);
        dp[i] = Time[i];
    }

    while (!q.empty())
    {
        int node = q.front();
        q.pop();

        for (int i = 0; i < graph[node].size(); i++)
        {
            int next = graph[node][i];

            if (--inDegree[next] == 0)
                q.push(next);
                
            dp[next] = max(dp[next], dp[node] + Time[next]);
        }
    }

}

<위상 정렬 및 dp 갱신 함수>
위에서 설명한 알고리즘에 따라, dp 갱신 값은

dp[next] = max(dp[next], dp[now] + TIME[next]);

가 된다.

🪄전체 코드

#define _CRT_SECURE_NO_WARNINGS
#include <iostream> // cpp
#include <algorithm>
// 자료 구조
#include <queue>
#include <vector>
using namespace std;

int n;
int Time[501];
int inDegree[501];
int dp[501];
vector<int> graph[501];

void INPUT()
{
    ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> Time[i];
        while (true)
        {
            int node; cin >> node;
            if (node == -1) break;
            graph[node].push_back(i);
            inDegree[i]++;
        }
    }
}

void topology()
{
    queue<int> q;

    for (int i = 1; i <= n; i++)
    {
        if (inDegree[i] == 0) q.push(i);
        dp[i] = Time[i];
    }

    while (!q.empty())
    {
        int node = q.front();
        q.pop();

        for (int i = 0; i < graph[node].size(); i++)
        {
            int next = graph[node][i];

            if (--inDegree[next] == 0)
            {
                q.push(next);
            }
            dp[next] = max(dp[next], dp[node] + Time[next]);
        }
    }

}

void SOLVE()
{
    topology();

    for (int i = 1; i <= n; i++) cout << dp[i] << "\n";
}


int main()
{
    INPUT();

    SOLVE();
}

🥇문제 후기

ACM Craft 문제랑 완전히 똑같다.
ACM Craft 문제 풀이 링크이다.
복붙잼