백준 1707번 이분 그래프

🔒[문제 url]

https://www.acmicpc.net/problem/1707

🔑알고리즘

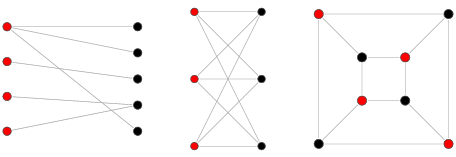
• 이분(二分) 그래프란?
  • 인접한 정점끼리 색이 다르고, 모든 정점을 두 가지 색으로만 칠할 수 있는 그래프.

1. DFS(BFS도 무방)탐색을 진행하며, 각 정점을 방문할때마다 true와 false를 번갈아가며 표시한다.
2. DFS 탐색을 다시 진행하며, 각 정점이 인접한 정점들과의 표시값을 확인한다.
   - 모든 정점이 인접한 정점과 표시값이 다르면 이분 그래프이고, 같으면 이분 그래프가 아니다.
   
   

• 탐색 중 주의할 점은?
  • 테스트 케이스가 반복되는 문제이고, 하나의 케이스에 두 번의 DFS탐색이 진행되기 때문에 초기화에 신경쓰도록 하자.

🐾부분 코드

void markDFS(int node, bool mark)
{
	/*
	각 정점을 방문할때마다 true와 false를 번갈아가며 표시한다.
	이분 그래프의 성질을 만족하기 위해선,
	한 정점이 인접한 정점과 같은 표시값을 가지면 안 된다.

	DFS를 두번 진행한다.
	표시 -> 표시값 확인
	*/
	check[node] = mark;
	visited[node] = true;

	for (int i = 0; i < map[node].size(); i++)
		if (!visited[map[node][i]]) markDFS(map[node][i], !mark);
}

<정점에 mark하는 DFS 함수>
표시할 bool 값인 mark변수를 인자로 받아줌으로써, 각 정점에 방문할때마다 표시해준다. 이후 for문으로 인접한 정점에 !mark를 넘겨줌으로써 표시값을 번갈아가며 표시한다.

void checkDFS(int node)
{// 이분 그래프 판별 DFS

	visited[node] = true;

	for (int i = 0; i < map[node].size(); i++)
	{
		if (check[node] == check[map[node][i]])
		{// 이전 지점의 표시값과 현재 지점의 표시값과 같으면
			isBG = false;
			return;
		}
		else if (!visited[node])
		{
			checkDFS(node);
		}
	}

}

<이분 그래프 판별 DFS>
각 정점을 방문하며, 인접한 모든 정점 중 같은 표시값이 발견되면
즉시 isBG(이분 그래프이면 True)값을 false로 설정하고 탐색을 종료한다.

void SOLVE()
{
	while (k--)
	{
		
		// INPUT
		cin >> v >> e;
		for (int i = 0; i < e; i++)
		{
			int a, b; cin >> a >> b;
			map[a].push_back(b); map[b].push_back(a);
		}

		// 표시하기
		for(int i = 1; i <= v; i++)
			for (int j = 0; j < map[i].size(); j++)
			{
				if (!visited[i])
					markDFS(i, true);
			}

		// 방문 기록 초기화 후 이분 그래프 판정하기
		for (int i = 0; i < 20001; i++) visited[i] = false;
		for (int i = 1; i <= v; i++)
		{
			for (int j = 0; j < map[i].size(); j++)
			{
				if (!visited[i])
				{
					checkDFS(i);
					if (!isBG) break;
				}
			}
			if (!isBG) break;
		}

		// 출력
		if (isBG) cout << "YES\n";
		else cout << "NO\n";

		// 초기화
		isBG = true;
		for (int i = 0; i < 20001; i++) visited[i] = false;
		for (int i = 0; i < 20001; i++) check[i] = false;
		for (int i = 1; i <= v; i++) map[i].clear();
	}
}

<입출력, 초기화 및 테스트 케이스 반복 함수>
markDFS와 checkDFS 사이에 방문 기록을 초기화한다.
탐색 후 isBG 값에 따라 답을 출력한다.

하나의 Test Case가 종료되면, 모든 변수를 초기화한 후 다음 Test Case를 진행한다.

🪄전체 코드

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <string>
#include <algorithm>
#include <cmath>
#include <queue>
#include <vector>
#include <stdio.h>
#include <ctime>
#include <memory.h> // memset
#include <numeric>
#include <stack>
#include <sstream>
using namespace std;
/* –2,147,483,648 ~ 2,147,483,647 */

int k, v, e;
vector<int> map[20001];
vector<bool> check(20001); // true false 번갈아가며 표시
vector<bool> visited(20001);

bool isBG = true;

void INPUT()
{
	ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	cin >> k;
}

void markDFS(int node, bool mark)
{
	/*
	각 정점을 방문할때마다 true와 false를 번갈아가며 표시한다.
	이분 그래프의 성질을 만족하기 위해선,
	한 정점이 인접한 정점과 같은 표시값을 가지면 안 된다.

	DFS를 두번 진행한다.
	표시 -> 표시값 확인
	*/
	check[node] = mark;
	visited[node] = true;

	for (int i = 0; i < map[node].size(); i++)
		if (!visited[map[node][i]]) markDFS(map[node][i], !mark);
}

void checkDFS(int node)
{// 이분 그래프 판별 DFS

	visited[node] = true;

	for (int i = 0; i < map[node].size(); i++)
	{
		if (visited[node] &&
			check[node] == check[map[node][i]])
		{// 이전 지점의 표시값과 현재 지점의 표시값과 같으면
			isBG = false;
			return;
		}
		else if (!visited[node])
		{
			checkDFS(node);
		}
	}

}

void SOLVE()
{
	while (k--)
	{
		
		// INPUT
		cin >> v >> e;
		for (int i = 0; i < e; i++)
		{
			int a, b; cin >> a >> b;
			map[a].push_back(b); map[b].push_back(a);
		}

		// 표시하기
		for(int i = 1; i <= v; i++)
			for (int j = 0; j < map[i].size(); j++)
			{
				if (!visited[i])
					markDFS(i, true);
			}

		// 방문 기록 초기화 후 이분 그래프 판정하기
		for (int i = 0; i < 20001; i++) visited[i] = false;
		for (int i = 1; i <= v; i++)
		{
			for (int j = 0; j < map[i].size(); j++)
			{
				if (!visited[i])
				{
					checkDFS(i);
					if (!isBG) break;
				}
			}
			if (!isBG) break;
		}

		// 출력
		if (isBG) cout << "YES\n";
		else cout << "NO\n";

		// 초기화
		isBG = true;
		for (int i = 0; i < 20001; i++) visited[i] = false;
		for (int i = 0; i < 20001; i++) check[i] = false;
		for (int i = 1; i <= v; i++) map[i].clear();
	}
}

int main()
{
	INPUT();

	SOLVE();
}

🥇문제 후기

이분 그래프의 개념을 간단하게 보고 풀이를 시작했다. 쉬운 개념덕에 풀이 방법또한 금방 떠올라 쉽게 풀었던 문제.
정점의 번호가 1번부터 시작하기때문에 v(정점의 개수)만큼 탐색할때 범위를 1 <= i <= v 로 잡아야하는데, 0 <= i < v로 잡아 시간이 조금 뺏겼다. 그래도 초기화 작업은 깔끔하게 처리해서 만족했다!
결론: 촉박한 상황에서도 변수의 범위는 잘 읽도록하자!