백준 2133번 타일 채우기

🔒[문제 url]

https://www.acmicpc.net/problem/2133

🔑알고리즘

이전에 채운 타일에 새로운 타일을 어떻게 추가하느냐를 떠올리는게 핵심이었다.
따라서 Dynamic Programming으로 접근한다.

몇 가지 예시를 살펴보며 점화식을 도출해보자.

• N이 홀수일때, 타일 배치의 경우의 수는 0이다.
  
  
• N = 2일때 배치 종류는 다음과같이 3이다.
  
  
• N = 4일때 배치 종류는 위에서 살펴본 N = 2의 종류끼리 연결한 2 2형태. 즉, 3종류 X 3종류 = 9에,
  아래와같은 새로운 타일 배치 두 종류가 추가되어 9 + 2 =11이다.
  
  
• N = 6일때, 타일 배치의 경우의 수는 N = 4 배치와 N = 2 배치의 조합인
  11종류 X 3종류 = 33에, N = 2 배치에 N = 4에서 새로 추가된 두 종류의 조합인
  3종류 X 2종류 = 6을 더하고,
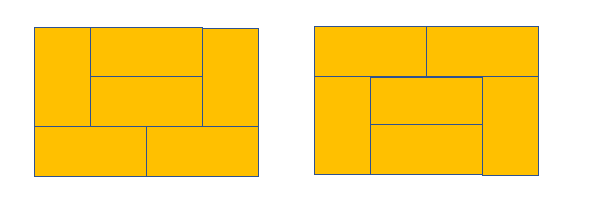
  아래와같은 새로운 두 종류가 추가되어 33 + 6 + 2 =41이다.
  
  
• 그렇다면 점화식dp[i] : N = i 일때 가능한 타일 배치의 수은?
  • N = i일때, N = i - 2 배치와 N = 2 배치를 조합할 수 있으므로,
    dp[i] += 3 x dp[i - 2];
  • N = i일때, 2 <= j <= i - 4인 j에 대하여,
    N = j일때 추가된 새로운 두 종류의 배치와 N = i - j 배치를 조합할 수 있으므로, dp[i] += 2 x dp[i - j];
  • N >= 4이라면 새로운 배치가 두 종류씩 추가된다. dp[i] += 2;

🪄전체 코드

#define _CRT_SECURE_NO_WARNINGS
#include <iostream> // cpp
using namespace std;

int n;
int dp[31]{ 0, };

void INPUT()
{
	ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	cin >> n;
}

void SOLVE()
{
	// 초기 작업
	dp[2] = 3; dp[4] = 11;

	for (int i = 6; i <= n; i += 2)
	{
		// i-2길이의 타일에 2길이 타일 종류만큼 곱
		dp[i] += 3 * dp[i - 2];

		for (int j = 2; j < i - 2; j += 2)
			// j길이 타일에서 추가된 새로운 타일의 종류만큼 곱
			dp[i] += 2 * dp[j];

		dp[i] += 2; // 새로운 타일
	}
	cout << dp[n];
}

int main()
{
	INPUT();

	SOLVE();
}

점화식 이해되었다면 코드 작성은 간단하므로 부분 코드는 생략한다.

🥇문제 후기

DP 포스팅 너무 힘들어요 빼ㅐㅐ액.. 그래도 DP 숙련도는 늘고있다!